Шамышева2 / ОСНОВЫ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ (Конспект лекций)

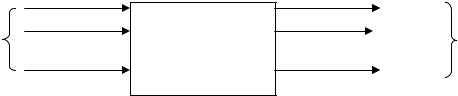
щие состояние системы в каждый данный момент времени, называются пе-

ременными состояния системы.

Множество всех возможных входных сигналов системы называют ее

пространством входных сигналов. Множество всех возможных выходных сигналов – пространством выходных сигналов. Вектором состояния назы-

вают всю совокупность переменных состояния системы.

Входные и выходные сигналы системы как определенные функции вре-

мени, а также изменение вектора состояния со временем характеризуют

функционирование или состояние системы.

Основной характеристикой системы является ее оператор, опреде-

ляющий механизм формирования выходного сигнала по данному входному сигналу. Оператор детерминированной системы ставит в соответствие каж-

дому входному сигналу один определенный выходной сигнал – т.о. отобра-

жает пространство входных сигналов X в пространство выходных сигналов

Y.

Соотношение между входными и выходными сигналами детерминиро-

ванной системы можно записать в виде операторного уравнения :

у(t) = Ax(t).

Детерминированная система называется физически возможной, если значение ее выходного сигнала у(t) в каждый момент времени t не зависит от значений входного сигнала x(τ) при τ>t. Таким образом, значение выходного сигнала физически возможной системы у(t) в каждый момент t является функционалом от входного сигнала x(τ), заданного в интервале t0≤ τ≤ t.

В практических задачах приходится встречаться с различными матема-

тическими описаниями входных и выходных сигналов. Так, в автоматиче-

11

ских системах входные и выходные сигналы с математической точки зрения представляют скалярные или векторные функции, в конечных автоматах – логические переменные, в системах массового обслуживания – потоки собы-

тий, в системах распознавания – изображения и др. образы. В стохастических системах входные и выходные сигналы считаются элементами произвольных абстрактных пространств.

Действие системы состоит в том, что данному элементу x пространства входных сигналов Х она ставит в соответствие некоторый элемент у про-

странства выходных сигналов Y.

Стохастической системой называется такая система, которая ставит в соответствие любому входному сигналу x€X определенное распределение ве-

роятностей в пространстве выходных сигналов Y. Поведение стохастической системы описывается переходной вероятностью

μy = μ(Ey|x)

принадлежности выходного сигнала множеству Ey€Y при данном входном сигнале x€X. Функция μy называется условно вероятностной мерой или ре-

шающей функцией системы. При каждом x€X она представляет собой нор-

мированную меру, определенную на некоторой σ – алгебре B множеств про-

странства Y, и при каждом множестве Ey€B является функцией переменной х,

измеримой относительно σ – алгебры А пространства Х.

Решающая функция – это достаточно полная вероятностная характери-

стика стохастической системы. В приложениях часто ограничиваются менее полными характеристиками, например условными многомерными плотно-

стями и характеристическими функциями, условными моментами различных порядков.

Стохастическая система называется физически возможной, если рас-

пределение значения ее выходного сигнала Y(t) в любой момент t не зависит от значений входного сигнала x(τ) при τ>t.

Пусть задан некоторый невозмущенный входной сигнал x(t) системы и пусть у(t) – соответствующий ему выходной сигнал, который назовем невоз-

12

мущенным. Всякий другой сигнал x| (t) будем называть возмущенным вход-

ным сигналом, а соответствующий ему выходной сигнал – у| (t) – возмущен-

ным выходным сигналом. Отклонение входного и выходного сигналов от не-

возмущенных определим как

x(t)= x| (t)- x(t) и у(t)= у| (t)- у(t).

Стохастическая система называется устойчивой относительно задан-

ного невозмущенного сигнала почти наверное (с вероятностью 1), если от-

клонение ее выходного сигнала Y(t) сколь угодно мало с вероятностью 1

при любом достаточно малом отклонении входного сигнала x(t).

Стохастическая система называется устойчивой относительно задан-

ного невозмущенного сигнала в р-среднем, p>0, если математическое ожи-

дание M| Y(t)|p остается сколь угодно малым при всех достаточно малых отклонениях входного сигнала x(t). Из устойчивости почти наверно вытека-

ет устойчивость по вероятности.

Наибольшее значение для приложений имеет понятие устойчивости почти наверное (устойчивость для всех реализаций происходящих в системе процессов). В практических задачах ограничиваются устойчивостью в сред-

нем (р=1) и в среднем квадратическом (р=2).

При исследовании стохастических систем следует учитывать, что связи в этих системах в общем случае также являются стохастическими в смысле,

что они могут случайно возникать и нарушаться в процессе работы системы.

Поток событий, управляющий случайными изменениями связей в сложной системе или изменением состояния системы, можно рассматривать как выходной сигнал некоторой стохастической системы и в то же время как дополнительную компоненту входного сигнала данной системы. Это дает возможность свести систему со случайными изменениями связей к последо-

вательному соединению двух систем.

Пример. Рассмотрим системы со случайно изменяющейся структурой. Ими еалиются стохастические системы, которые описываются различными уравнениями в разных областях пространства состояния. К изучению таких систем сводятся задачи потери управления, срыва слежения вследствие ограниченности диапазона изменения пере-

менных состояния, в которых система может функционировать и др.

13

1.3. Моделирование сложных (стохастических) систем

Для получения математической модели необходимо установить соот-

ношение между входными, выходными сигналами и вектором состояния системы. Эти соотношения могут быть детерминированными или содержать некоторые элементы неопределенности. В последнем случае пользуются ве-

роятностным подходом, приписывая случайный (стохастический) характер и соответствующие распределения всем неопределенным величинам. Таким образом, приходим к следующему определению математической модели сис-

темы.

Математической моделью системы называется совокупность четырех элементов:

1) пространства состояний, 2) пространства входных сигналов, 3) про-

странства выходных сигналов и 4) соотношений, связывающих входной и выходной сигналы и вектор состояния системы.

Классификация систем по типу поведения [2]

Общее абстрактное описание (абстрактная модель) лишь отражает ха-

рактер описания и общие свойства систем широкого класса с различным ти-

пом поведения. Для построения модели удобнее использовать некоторые ти-

повые математические схемы, отражающие те или иные типы поведения ре-

альных моделируемых систем.

По числу состояний модели делятся на статические и динамические.

Для статических моделей характерным является то, что выход системы (или ее характеристики) в некоторый момент времени определяется значением входного сигнала в тот же момент времени: .

В плане абстрактного описания эти системы можно определить как системы с одним значением состояния, то есть предыстория не изменяет со-

стояния и, стало быть, не влияет на выход. Если возможных состояний мно-

жество, то систему (и модель) классифицируют как динамическую.

Динамические модели (системы) следует различать по времени пере-

хода их из состояния в состояние, что обычно определяется характером мно-

15

жества Т значений времени, которое интересует исследователя. Если Т счет-

ное множество значений, то имеет место описание в дискретном времени и модель (систему) называют моделью (системой) с дискретным временем.

Соответственно, если Т несчетное множество, то моделью (системой) с

непрерывным временем.

По типу состояний (по типу множества значений Х) системы (модели)

разделяют на системы (модели) с дискретным состоянием, если множество

Х есть конечное счетное множество, и на системы (модели) с непрерывным состоянием, если Х несчетное множество (множество обладает мощностью континуума).

По условиям переходов систем из состояния в состояние они могут быть разделены на детерминированные и стохастические.

Если модель путем применения к ней формальных процедур позволяет однозначно предсказать изменение состояния и, соответственно, выхода, то модель называют детерминированной.

Если удается оценить лишь статистические характеристики этих пере-

менных, то модель называют стохастической . Такие модели обычно имеют место при необходимости учета различного рода случайных факторов, таких как случайные входы, случайные параметры, случайные начальные условия,

с целью отражения присущей моделируемой реальной системе неопределен-

ности поведения, или неполноты информации о системе.

Статистические и теоретико-вероятностные методы составляют методологическую основу одноименного вида моделирования. На этом уров-

не формализации модели речь о вскрытии закона, обеспечивающего устране-

ние неопределенности при принятии решения, пока еще не идет, но сущест-

вует некоторый массив наблюдений за данной системой или ее аналогом, по-

зволяющих сделать некие выводы относительно прошло-

го/текущего/будущего состояния системы, основываясь на гипотезе об инва-

риантности (неизменности) ее поведения.

16

Как всегда, сформулируем определение… Статистическая или тео-

ретико-вероятностная модель (стохастическая модель) — это модель, в

которой обеспечивается учет влияния случайных факторов в процессе функционирования системы, основанная на применении статистической или теоретико-вероятностной методологии по отношению к повторяющимся феноменам. Данная модель оперирует количественными критериями при оценке повторяющихся явлений и позволяет учитывать их нелинейность, ди-

намику, случайные возмущения за счет выдвижения на основе анализа ре-

зультатов наблюдений гипотез о характере распределения некоторых слу-

чайных величин, сказывающихся на поведении системы.

По существу, теоретико-вероятностные и статистические модели отли-

чаются уровнем неопределенности знаний о моделируемой системе, сущест-

вующей на момент синтеза модели. В случае, когда представления о системе носят, скорее, теоретический характер и основываются исключительно на гипотезах о характере системы и возмущающих воздействий, не подкреплен-

ных результатами наблюдений, теоретико-вероятностная модель является единственно возможной.

Когда же на этапе синтеза модели уже существуют данные, получен-

ные опытным путем, появляется возможность подкрепления гипотез за счет их статистической обработки. Это становится очевидным, если рассмотреть соотношение между методами математической статистики и теории вероят-

ностей.

Математическая статистика — это наука, изучающая методы вскрытия закономерностей, свойственных большим совокупностям однород-

ных объектов или событий, на основании их выборочного обследования (ли-

бо большим массивам данных, полученных в результате наблюдения за од-

ним и тем же объектом на протяжении достаточно протяженного интервала времени).

Теория вероятностей изучает количественные закономерности, кото-

рым следуют случайные явления, если эти явления определяются событиями

17

известной вероятности. Соответственно, математическая статистика является связующим звеном между теорией вероятностей и явлениями реального ми-

ра, поскольку позволяет сформулировать оценки вероятности тех или иных событий на основе анализа статистических данных.

Можно утверждать, что статистические модели представляют собой особый вид математических моделей, использующих в качестве исходных данных не только актуальные данные о текущем состоянии объекта, но и данные, характеризующие состояние либо других объектов данного класса,

либо этого объекта, но в иной момент времени.

Статистическое моделирование тесно сопряжено с имитационным моделированием, в ходе которого модель объекта нередко «погружается в ве-

роятностную (статистическую) среду», в которой проигрываются различные ситуации и режимы функционирования модели/объекта. Имитационные мо-

дели могут реализовываться и в детерминированных средах.

Имитационная модель – это формальное (т.е. выполненное на неко-

тором формальном языке) описание логики функционирования исследуемой системы и взаимодействия, отдельных ее элементов во времени, учитываю-

щее наиболее существенные причинно-следственные связи, присущие систе-

ме, и обеспечивающие проведение статистических экспериментов.

Остановимся более подробно на понятии статистический экспери-

мент.

В его основе лежит метод статистических испытаний (метод Монте-

Карло). Суть его состоит в том, что результат испытания ставится в зависи-

мость от значения некоторой случайной величины, распределенной по задан-

ному закону. Поэтому результат каждого отдельного испытания также носит случайный характер.

Проведя серию испытаний, получают множество частных значений на-

блюдаемой характеристики (т.е. выборку). Полученные статистические дан-

ные обрабатываются и представляются в виде соответствующих численных оценок интересующих исследователя величин (характеристик системы).

18

Теоретической основой метода статистических испытаний являются предельные теоремы теории вероятностей (теорема Чебышева, теорема Пу-

ассона, теорема Бернулли). Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом числе испытаний.

Важно отметить, что метод статистических испытаний применим для исследования как стохастических , так и детерминированных систем.

Еще одной важной особенностью данного метода является то, что его реализация практически невозможна без использования компьютера.

Поскольку основой имитационного моделирования является метод статистических испытаний, то наибольший эффект от его применения еатигается при исследовании сложных систем, на функционирование кото-

рых существенное влияние оказывают случайные факторы.

Применение имитационного моделирования целесообразно в следую-

щих случаях:

если не существует законченной постановки задачи на исследование и идет процесс познания объекта моделирования;

если характер протекающих в системе процессов не позволяет описать эти процессы в аналитической форме;

если необходимо наблюдать за поведением системы (или отдельных ее компонентов) в течение определенного периода, в том числе с изменением скорости протекания процессов;

при изучении новых ситуаций в системе либо при оценке функциониро-

вания ее в новых условиях;

если исследуемая система является элементом более сложной системы,

другие элементы которой имеют реальное воплощение;

когда необходимо исследовать поведение системы при введении в нее но-

вых компонентов;

при подготовке специалистов и освоении новой техники (в качестве тре-

нажеров).

19

Приведенный список возможных областей применения имитационных моделей можно рассматривать и как перечень их достоинств, но, к сожале-

нию, имитационные модели имеют и ряд недостатков. Первый, и весьма су-

щественный, заключается в том, что разработка имитационных моделей, как правило, требует больших затрат времени и сил. Кроме того, любая имита-

ционная модель сложной системы значительно менее объективна, чем анали-

тическая модель, поскольку она, прежде всего, отражает субъективные пред-

ставления разработчика о моделируемой системе. И, наконец, результаты имитационного моделирования, как и при любом численном методе, всегда носят частный характер. Для получения обоснованных выводов необходимо проведение серии модельных экспериментов, а обработка результатов требу-

ет применения специальных статистических процедур.

Стохастическим программированием называют метод решения оптимизационных задач, в которых целевая функция недоступна для вычис-

ления в чистом виде, а может быть оценена или вычислена с погрешностью,

например из эмпирических наблюдений или экспериментов. Стохастиче-

ское программирование может применяться для решения задач оценки па-

раметров стохастических объектов, управления, динамической идентифика-

ции, однако, в отличие от прямых методов решения этих задач, стохастиче-

ское программирование не требует хранения всей накопленной информа-

ции об объекте, а предлагает способ адаптивной коррекции оценки по дан-

ным следующего наблюдения. Рассматриваются такие методы как Робинса– Монро, Киффера–Вольфовица, конечно-сходящиеся алгоритмы, методы случайного поиска. Кроме того, рассматриваются нейросетевые и генетиче-

ские алгоритмы, как частные случаи алгоритмов стохастического еалии ямирования для решения специфических задач.

Контрольные вопросы:

1)В чем заключается функционирование системы?

2)Что характеризуют функционирование или состояние системы?

20