Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владимирский государственный университет им. Столетовых

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Шамышева2 / ОСНОВЫ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ (Конспект лекций)

.pdf

Скачиваний:

105

Добавлен:

22.03.2015

Размер:

5.33 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

(xi

x )( yi

(xi x )( yi

y )

rx, y

Cov( X ,Y ) n 1 i 1

i 1

, (8.1)

(xi x )

( yi y)

i 1

где

S 2

(x x )2

S 2

( y y)2 - оценки дисперсий величин

n 1

X и Y .

Проверка значимости парного коэффициента корреляции

Для оценки значимости коэффициента корреляции применяется t –

критерий Стьюдента. При этом фактическое значение этого критерия

еалии яяется по формуле:

		r2
tнабл		y,x	(n 2)
tнабл		2	(n 2)	(8.2)
	1	ry,x
Вычисленное по этой формуле значение				tнабл сравнивается с крити-

ческим значением t-критерия, которое берется из таблицы значений t –

Стьюдента с учетом заданного уровня значимости и числа степеней свободы.

Если tнабл > tкр, то полученное значение коэффициента корреляции признается значимым (то есть нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.

Коэффициенты парной корреляции используются для измерения силы линейных связей различных пар переменных из их множества. Для множест-

ва m переменных n наблюдений получают матрицу коэффициентов парной корреляции R.

r	r	...	r
11	12		1m
R	r22	...	r2m	(8.3)
R		...		(8.3)
..... .....		...	......

..... .....		...	rmm

101

Одной корреляционной матрицей нельзя полностью описать зависимо-

сти между величинами. В связи с этим, в многомерном корреляционном еаллизе рассматривается две задачи:

1.Определение тесноты связи одной случайной величины с совокуп-

ностью остальных (m – 1) величин, включенных в анализ;

2.Определение тесноты связи между величинами при фиксировании или исключении влияния остальных k величин, при k<(m-2).

Эти задачи решаются с помощью коэффициентов множественной и частной корреляции, соответственно.

Множественный коэффициент корреляции

Решение первой задачи осуществляется с помощью выборочного ко-

эффициента множественной корреляции по формуле

R j,1,2, j 1, j 1,...m	1		R	,	(8.4)

		R jj
		R jj

где R - определитель корреляционной матрицы R (8.3);

R jj - алгебраическое дополнение элемента rjj той же матрицы R.

Квадрат коэффициента множественной корреляции R2 j,1,2, j 1, j 1,...,m

принято называть выборочным множественным коэффициентом детерминации, который показывает, какую долю вариации (случайного разброса) исследуемой величины Хj объясняет вариация остальных случайных величин X1 , X2 , . . . , Xm.

Коэффициенты множественной корреляции и детерминации являются величинами положительными, принимающими значения в интервале от 0 до 1. При приближении коэффициента R2 к единице можно сделать вывод о тесноте взаимосвязи случайных величин, но не о ее направлении. Коэффициент множественной корреляции может только

102

увеличиваться, если в модель включать дополнительные переменные и не увеличится, если из имеющихся переменных производить исключение.

Проверка значимости коэффициента множественной корреляции осуществляется путем сравнения расчетного значения критерия Фишера:

Fрасч		R2 / n m			,	(8.5)
		R2	/
	1			m 1

с табличным Fтабл. Табличное значение критерия определяется заданным уровнем значимости и степенями свободы k1 m 1 и k2 n m . Коэф-

фициент R2 значимо отличается от нуля, если выполняется неравенство

Fpаас Fтабл .

Частный коэффициент корреляции

Если рассматриваемые случайные величины коррелируют друг с дру-

гом, то на величине коэффициента парной корреляции частично сказывается влияние других величин. В связи с этим возникает необходимость исследо-

вания частной корреляции между величинами при исключении влияния од-

ной или нескольких других случайных величин.

Выборочный частный коэффициент корреляции определяется по фор-

муле:

rjk.1,2, ,m			R jk

			,
			R jj Rkk

где R jk , R jj , Rkk – алгебраические дополнения к соответствующим элемен-

там матрицы (8.3).

Частный коэффициент корреляции, так же как и парный коэффициент корреляции изменяется от –1 до +1.

Пример 8.1. Вычисление коэффициентов парной, множественной и частной корреляции.

103

В табл. 8.1. приведена информация об объёмах продаж и затратах на рекламу одной фирмы, а также индекс потребительских расходов за ряд текущих лет.

Требуется:

1.Построить диаграмму рассеяния (корреляционное поле) для переменных «объёмы продаж» и «индекс потребительских расходов».

2.Определить степень влияния индекса потребительских рас-

ходов на объёмы продаж (вычислить коэффициент парной корреля-

ции).

3.Оценить значимость вычисленного коэффициента парной корреляции.

4.Построить матрицу коэффициентов парной корреляции по трем переменным.

5.Найти оценку множественного коэффициента корреляции.

6.Найти оценки коэффициентов частной корреляции.

Решение

1) Вытянутость облака точек на диаграмме рассеяния вдоль наклонной прямой позволяет сделать предположение о том, что существует некоторая объективная тенденция прямой линейной связи между значениями перемен-

ных X- индекс потребительских расходов и Y- объёмы продаж.

В нашем примере диаграмма рассеяния имеет вид, приведенный на рис. 8.1.

Таблица 8.1

Объем	продаж,	126	137	148	191	274	370	432	445	367	367	321	307	331	345	364	384
тыс. руб.-Y
Затраты	на рек-	4	4,8	3,8	8,7	8,2	9,7	14,7	18,7	19,8	10,6	8,6	6,5	12,6	6,5	5,8	5,7
ламу – Х1
Индекс потреби-				101,	103,	104,		107,	108,	108,	109,	110,	110,	110,	111,	112,	112,
тельских	расхо-	100	98,4	101,	103,	104,	107	107,	108,	108,	109,	110,	110,	110,	111,	112,	112,
дов, % - X2				2	5	1		4	5	3	2	1	7	3	8	3	9
дов, % - X2

104

2) Промежуточные расчеты при вычислении коэффициента корреляции между переменными x- индекс потребительских расходов и y- объёмы про-

даж приведены в таблице 8.2.

Средние значения случайных величин Х и Y, которые являются наибо-

лее простыми показателями, характеризующими последовательности

x1 , x2 ,

, x16

и y1, y2 ,

, y16 ,

рассчитаем по формулам, соответственно:

107, 2

306,8 .

n i 1

Дисперсия характеризуют

степень

разброса

значений x1 , x2 , , x16

( y1, y2 ,

, y16 )

вокруг своего среднего x ( y

, соответственно)

Sx2

(xi x )2

305, 474

20,36

Sy2

( yi

y)2

158718, 438

10581,23.

n 1

Стандартные ошибки случайных величин Х и Y рассчитаем по форму-

лам, соответственно:

n 1 xi

4,51; Sy

n 1 yi

102,87

i 1

105

Объем продаж

500

450

400

350

300	107,2; 306,8

250

200

150

100

102

104

106

108

110

112

114

Индекс потребительских расходов

Рис. 8.1. Диаграмма рассеяния (корреляционное поле).

Коэффициент корреляции рассчитаем по формуле (8.1):

		1			n
		1			(xi	x )( yi y)					1	5681, 99
											1

r			n 1 i 1							15					= 0, 816
r															= 0, 816
x. y					Sx	Sy				4, 51 102, 87
					Sx	Sy				4, 51 102, 87
Таблица 3.2.
№	Y			X			y y	x x	( y y)(x x )					(x x )2		( y y)2
							i	i			i		i		i	i

1	126			100			-180,813	-7,231	1307,500					52,291		32693,160

2	137			98,4			-169,813	-8,831	1499,657					77,991		28836,285

3	148			101,2			-158,813	-6,031	957,838					36,376		25221,410

4	191			103,5			-115,813	-3,731	432,125					13,922		13412,535

5	274			104,1			-32,813	-3,131	102,744					9,805		1076,660

6	370			107			63,188	-0,231	-14,612					0,053		3992,660

7	432			107,4			125,188	0,169	21,125					0,028		15671,910

8	445			108,5			138,188	1,269	175,325					1,610		19095,785

9	367			108,3			60,188	1,069	64,325					1,142		3622,535

10	367			109,2			60,188	1,969	118,494					3,876		3622,535

11	321			110,1			14,188	2,869	40,700					8,230		201,285

12	307			110,7			0,188	3,469	0,650					12,032		0,035

106

13	331	110,3	24,188	3,069	74,225	9,417	585,035

14	345	111,8	38,188	4,569	174,469	20,873	1458,285

15	364	112,3	57,188	5,069	289,869	25,692	3270,410

16	384	112,9	77,188	5,669	437,557	32,135	5957,910

сумма	4909	1715,7	0,000	0,000	5681,994	305,474	158718,438

среднее	306,8125	107,23125

3) Оценим значимость коэффициента корреляции. Для этого рассчита-

ем значение t – статистики по формуле

	r	n	2
tрасч	r	n	2	0,816	14	5, 282.


	1		r2	1	0,666
	1		r2	1	0,666

Табличное значение критерия Стьюдента равно: tтабл (α = 0,1; k = n – 2

= 14) =1,76. Сравнивая числовые значения критериев, видно, что tрасч > tтабл,

т.е. полученное значение коэффициента корреляции значимо.

Таким образом, индекс потребительских расходов оказывает весьма высокое влияние на объёмы продаж.

4) Матрица R коэффициентов парной корреляции, вычисленных по формуле (8.1) для трех факторов будет иметь вид:

		Объем	Затраты на	Индекс потреби-
		еалиизации	рекламу	тельских расходов
		1	2	3

Объем реализации	1	1	0,646	0,816
Затраты на рекламу	2	0,646	1	0,273
Индекс потребительских расхо-	3	0,816	0,273	1
дов	3	0,816	0,273	1
дов

5) Вычисление множественного коэффициента корреляции y c x1 и

x2.

					R
R	j,1,2,	j 1, j 1,...m	1			1	0,1304	0, 9269
							0,1304

				Rjj		0, 9253
				Rjj		0, 9253

R - определитель корреляционной матрицы R равен 0,1304.

107

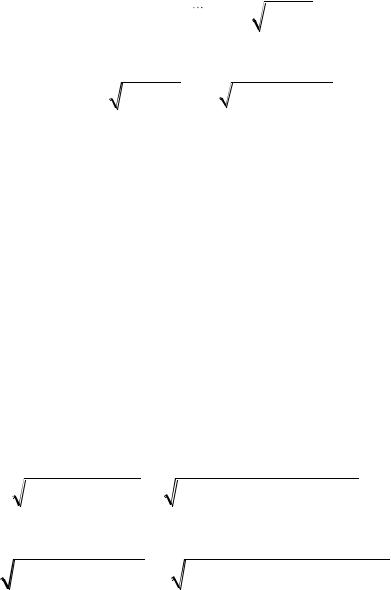
R11 - алгебраическое дополнение 1-го диагонального элемента r11 той же матрицы R

R ( 1)2					1		0, 273			0,9253		.
11				0, 273			1					.
				0, 273			1
6) Вычисление коэффициентов частной корреляции.
			rjk .1,2,		,m			Rjk

								Rjj Rkk
								Rjj Rkk
r12(3)			R12				0, 423				0, 706		,

			R11 R22			0,925 0,334
			R11 R22			0,925 0,334
где R12 алгебраическое дополнение элемента									r12 матрицы				R, а R22
алгебраическое дополнение 2-го диагонального элемента r22 :
							0, 273
		R ( 1)3			0, 646		0, 273		0, 423
	12				0,816		1
					0,816		1
	R22 ( 1)4						0,816			0,334 .
	R22 ( 1)4				1		0,816			0,334 .
					0,816		1

Коэффициенты частной корреляции можно вычислить, используя коэффициенты парной корреляции:

r12(3)		r12 r13		r23		0, 646 0,816 0, 273	0, 706

	(1		r2 ) (1 r2 )		(1 0,8162 ) (1 0.2732 )
			13	23

r13(2)		r13 r12			r23		0,816 0, 646 0, 273	0,871.

	(1		r2 )	(1 r2 )		(1 0, 6462 ) (1 0.2732 )
			12		23

Контрольные вопросы

1.Типы связей между переменными.

2.Основные задачи корреляционного анализа.

3.Мера взаимосвязи между двумя переменными и ее оценка.

108

4. Коэффициент парной корреляции его свойства.
5. Оценка выборочного коэффициента парной	корреляции по
статистическим данным.

6.Проверка значимости коэффициента парной корреляции.

7.Задачи, рассматриваемые в многомерном корреляционном анализе.

8.Коэффициент множественной корреляции, оценка его значимости.

9.Коэффициент частной корреляции, его оценка по статистическим

данным.

109

Лекция 9

ДИСПЕРСИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗЫ

9.1 ДИСПЕРСИОННЫЙ АНАЛИЗ

Во многих практических ситуациях представляет интерес влияние того или иного качественного фактора на рассматриваемый показатель. Влияет ли квалификация наладчиков на качество обслуживания ЭВМ? Влияет ли метод построения имитационных моделей на точность моделирования физической системы? Влияют ли примеси на качество стекловолокна? и др. Ответ на эти и аналогичные вопросы дается методами однофакторного дисперсионного анализа [5].

Пусть, например, качество программного продукта определяется с помощью k различных тестов и необходимо исследовать, влияет ли фактор «тест» на результат проверки. Если тестов два, то проверка гипотезы о средних показателей тестов проводится рассмотренными ранее методами проверки статистических гипотез о равенстве средних с использованием критерия Стьюдента. Если тестов более двух, то проверка гипотезы о равенстве средних показателей тестов проводится с использованием методов дисперсионного анализа.

Проверяется нулевая гипотеза Н0: m1=m2=..=mk об отсутствии влияния на результативный признак Х (результат тестирования) фактора А (тест), имеющего k уровней Aj , j=1, 2, …k.

Основная идея дисперсионного анализа состоит в том, чтобы сопоставить дисперсию за счет воздействия фактора А с дисперсией, обусловленной случайными причинами (остаточная дисперсия). Если различие между ними несущественно, то влияние фактора А на признак Х незначительно. Если же различие между факторной и остаточной дисперсиями значимо, то это говорит о влиянии фактора А на рассматриваемый признак Х.

Предполагается, что случайная величина Х имеет нормальное распределение с математическим ожиданием mj , зависящим от уровня фактора Aj и постоянной дисперсией σ2. В качестве исходных данных используются выборочные значения величины Х, полученные для каждого уровня фактора А; число элементов выборки на каждом уровне равно n, тогда общее число наблюдений равно nk. Обозначим через xij результат i-го наблюдения (i=1,2, … n) за j-м фактором.

Выборочное среднее, соответствующее j-у уровню фактора А (групповое среднее), вычисляется по формуле:

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1911 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в папке Шамышева2

#
22.03.20153.43 Mб43Лабораторные работы.pdf
#
22.03.20155.33 Mб105ОСНОВЫ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ (Конспект лекций).pdf
#
22.03.2015486.65 Кб35Основы теории стохастических систем.pptx
#
22.03.201510.28 Кб30файл пример корреляция.xlsx