
Шамышева2 / ОСНОВЫ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ (Конспект лекций)
.pdf
91

7.4 Определение статистических оценок математического ожидания и корреляционной функции случайного процесса
Рассмотрим случайный процесс как совокупность величин X(t). Мы можем в отношении каждой из них решать статистическую оценку интере-
сующих нас параметров: математических ожиданий M[X(t)] и корреляцион-
ных моментов RX(t1, t2), Для этого необходимо располагать достаточным чис-
лом независимых реализаций процесса X(t), полученных в одинаковых ус-
ловиях (например, осциллограммы). Для всех реализаций выбирается общее начало отсчета по параметру t, например, начало цикла по изучаемому про-
цессу.
Далее ось параметров разбивается на k равных интервалов, выбирая их длину так, чтобы на ее протяжении каждая реализация мало изменялась. При каждом значении ti в конце каждого интервала математическое ожидание
92
M[X(ti)] мы оцениваем по средней арифметической xcp(ti) |
из значений xi,1, xi,2, |
….xi,n величины полученных из n реализаций процесса. |
|
Получив ряд средних арифметических xcp(t1), xcp(t2), |
… xcp(tk), их ап- |
проксимируют подходящей кривой и, таким образом получают эмпириче-
скую оценку xcp(t), функции M[X(t)] – математического ожидания процесса.
При оценке корреляционного момента пользуются выше описанной
методикой, формула для вычислений |
имеет вид: |
|
RX |
cp(t1, t2) = 1/n∑ n |
[xl(t1) – xcp(t1)][xl(t2) – xcp(t2)] |
|
l=1 |
|
где n – число реализаций; t1, t2 выборочные параметры t; l – реализация процесса
1, 2, .. n.
Давая t1 и t2 все возможные значения получают ряд значений RX cp(t1, t2)
Аппроксимируя эти значения подходящей поверхностью в координатной системе t1, t2, RX(t1, t2) получают статистическую оценку корреляционной
функции. |
|
|
|
|
Аналогично |
определяют |
эмпирическое |
значение |
взаимной |
еалии яя онной функции двух случайных процессов X(t) и Y(t). Расчет-
ная формула имеет вид:
n
RXY cp(t1, t2) = 1/n∑ l=1 [xl(t1) – xcp(t1)][yl(t2) – ycp(t2)].
7.5 Стационарные случайные процессы
На практике часто встречаются случайные процессы, протекающие в вероятностном отношении однородно при изменении параметра времени t. К
числу таких процессов относятся помехи в линиях связи, ошибки в системах автоматического регулирования и др. Вероятностный режим таких процессов не изменяется при любом сдвиге всей группы точек t1, t2, ..ts вдоль числовой оси, т.е при переходе к точкам t1+τ, t2+τ, ..ts+τ, где τ произвольно выбранное
93
время. Поэтому, прежде всего, случайная величина X(t) для любого момента
имеет одно и то же распределение и, значит, имеет одинаковые математиче-
ские ожидания и дисперсии. Для процесса в целом M[X(t)]=const,
D[X(t)]=const, а автокорреляционная функция процесса непрерывна и зависит
только от разности t2 – t1=τ, т.е. является непрерывной функцией RX(τ) одного
аргумента τ. Такие случайные процессы называются стационарными случай-
ными процессами. Для стационарных процессов доказана сходимость по ве-
роятности среднего по времени от случайной функции:
Xcp T = 1/2T ∫ |
+T x(t)dt |
|
-T |
к математическому ожиданию M[X(t)] при T→∞.
Аналогично этому и для корреляционной функции доказана сходи-
мость по вероятности к величине
1/2T ∫ T-T x(t)x(t+τ)dt → RX(τ) при T→∞.
Точно так же для двух стационарных и стационарно связанных случай-
ных процессов X(t) и Y(t) доказывается сходимость по вероятности к еалии не :
1/2T ∫ T-T x(t)y(t+τ)dt → RXY (τ) при T→∞,
если x(t) и y(t) – возможные реализации процессов соответственно X(t) и Y(t).
Определение статистических оценок стационарного случайного про-
цесса можно производить не по множеству реализаций, а по единственной записи, если она охватывает большой интервал значений параметра времени
94
t. При этом на оси t откладывают n равных отрезков и в конце каждого из них определяются значения x1, x2., …xn.
Средняя арифметическая хср из них дает статистическую оценку мате-
матического ожидания случайного процесса.
Статистическая оценка автокорреляционной функции находится по формуле:
RX(τ) = 1/(n-τ)∑ n-τ (xl – xcp)(xl+τ – xcp).
l=1
Взаимная корреляционная функция двух стационарных процессов рас-
считывается по формуле:
RXY(τ) = 1/ (n-τ) ∑ n – τ (xl+τ – xcp)(yl – ycp).
l=1
Контрольные вопросы
1.Дайте определение случайного процесса.
2.Чем характеризуется случайный процесс. Сечение случайного
процесса.
3.Одномерный закон распределения мгновенных значений слу-
чайной функции и связанные с ним основные характеристики.
4.Многомерный закон распределения мгновенных значений слу-
чайной функции и связанные с ним основные характеристики.
5.Гауссовский случайный процесс и его характеристики.
6.Определение статистических оценок математического ожидания
икорреляционной функции случайного процесса.
7.Стационарные случайные процессы и их характеристики.
95

Лекция 8 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Корреляционный анализ, разработанный К. Пирсоном и Дж. Юлом яв-
ляется одним из методов статистического анализа взаимозависимости не-
скольких переменных – компонент случайного вектора.
Одним из основных показателей взаимосвязи двух случайных величин является парный коэффициент корреляции, служащий мерой линейной ста-
тистической зависимости между этими величинами, когда статистическая связь между соответствующими признаками в генеральной совокупности ли-
нейна.
Указанное условие выполняется, если генеральная совокупность рас-
пределена по многомерному нормальному закону.
1. Функциональные и корреляционные связи между переменными
Экспериментальные данные представляют собой количественные характери-
стики каких-либо объектов или процессов. Они формируются под действием множества факторов, не все из которых доступны контролю. Неконтроли-
руемые факторы могут принимать случайные значения из некоторого множе-
ства значений и тем самым обуславливать случайность данных, которые они определяют. Стохастическая природа экспериментальных данных обуслав-
ливает необходимость применения соответствующих статистических мето-
дов для их обработки и анализа.
Статистические распределения характеризуются наличием более или менее значительной вариации в величине измеренных переменных у отдельных единиц совокупности. Возникает вопрос о том, какие же причины формиру-
ют уровень переменной в данной совокупности и каков конкретный вклад каждой из них. Изучение зависимости вариации переменных от окружающих условий и составляет содержание теории корреляции.
96
Изучение действительности показывает, что вариация каждой переменной находится в тесной связи с вариацией других переменных, характеризующих исследуемую совокупность единиц. Вариация уровня производительности труда работников предприятий зависит от степени совершенства приме-
няемого оборудования, технологии, организации производства, труда и управления и других самых различных факторов.
При изучении конкретных зависимостей одни переменные выступают в каче-
стве факторов, обусловливающих изменение других переменных. Перемен-
ные этой первой группы будем называть факторными переменными; а пере-
менные, которые являются результатом влияния этих факторов, будем назы-
вать зависимыми (результативными).
Например, при изучении зависимости между производительностью труда ра-
бочих и энерговооруженностью их труда уровень производительности труда является результативной переменной, а энерговооруженность труда рабочих
– факторной переменной.
Рассматривая зависимости между переменными, необходимо выделить, пре-
жде всего, две категории зависимости: 1) функциональные и 2) корреляцион-
ные.
Функциональные связи характеризуются полным соответствием между изме-
нением факторной переменной и изменением результативной величины, и
каждому значению факторной переменной соответствуют вполне определен-
ные значения результативного переменной. Функциональная зависимость может связывать результативную переменную с одним или несколькими факторными переменными. Так, величина начисленной заработной платы при повременной оплате труда зависит от количества отработанных часов.
В корреляционных связях между изменением факторной и результативной пе-
ременными нет полного соответствия, воздействие отдельных факторов про-
является лишь в среднем при массовом наблюдении фактических данных.
Одновременное воздействие на изучаемую переменную большого количества
97
самых разнообразных факторов приводит к тому, что одному и тому же зна-
чению факторной переменной соответствует целое распределение значений результативной переменной, поскольку в каждом конкретном случае прочие факторные переменные могут изменять силу и направленность своего воз-
действия.
При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между пере-
менными можно, зная величину факторной переменной, точно определить величину результативной переменной. При наличии же корреляционной за-
висимости устанавливается лишь тенденция изменения результативной пе-
ременной при изменении величины факторной переменной. В отличие от же-
сткости функциональной связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции.
2. Корреляционный анализ
Основная задача корреляционного анализа заключается в выявлении взаимосвязи между случайными переменными путем точечной и интерваль-
ной оценки парных (частных) коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детер-
минации. Кроме того, с помощью корреляционного анализа решаются сле-
дующие задачи:
- отбор факторов, оказывающих наиболее существенное влияние на ре-
зультативную переменную, на основании измерения степени связи между ними; -
- обнаружение ранее неизвестных причинных связей.
Корреляция непосредственно не выявляет причинных связей между переменными, но устанавливает численное значение этих связей и достовер-
ность суждений об их наличии.
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
98
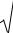
Ковариация между |
двумя переменными X и Y рассчитывается |
||
следующим образом: |
|
|
|
|
1 |
n |
|
Cov( X ,Y ) |
(xi x )( yi y) , |
||
|
|||
|
n 1 i 1 |
||
где (x1, y1), (x2 , y2 ),...,(xn , yn ) - фактические значения случайных
переменных X и Y,
|
1 |
n |
|
1 |
n |
|
y |
yi . |
x |
xi . |
|||
|
|
|||||
|
|
|||||
|
n i 1 |
|
n i 1 |
|||
Ковариация – это статистическая мера взаимодействия двух случайных переменных, таких, например, как доходности двух ценных бумаг.
Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют тенденцию изменяться в одну сторону.
Ковариация зависит от единиц, в которых измеряются переменные
X и Y . Поэтому для измерения силы связи между двумя переменными ис-
пользуется другая статистическая характеристика, называемая коэффициен-
том корреляции.
При проведении корреляционного анализа вся совокупность данных рассматривается как множество переменных (факторов), каждая из которых содержит n –наблюдений; хik – i-ое наблюдение k-ой переменной. Основными средствами анализа данных являются парные коэффициенты корреляции,
частные коэффициенты корреляции и множественные коэффициенты кор-
реляции.
Коэффициент парной корреляции
Для двух переменных X и Y теоретический коэффициент корреляции опре-
деляется следующим образом:
ρx,y |
x, y |
|||
|
|
|
. |
|
|
|
|
||
2 2 |
||||
|
x y |
|||
99
Где x 2 , y 2 - дисперсии случайных переменных X и Y , а x, y их кова-
риация.
Коэффициент парной корреляции является показателем тесноты свя-
зи лишь в случае линейной зависимости между переменными и обладает сле-
дующими основными свойствами:
1) Коэффициент корреляции принимает значение в интервале (-1,+1),
или
| xy| < 1.
2) Коэффициент корреляции не зависит от выбора начала отсчета и единицы измерения, т.е.
(α1X+β; α2Y+β)= xy,
где α1, α2, - постоянные величины, причем α1>0, α2>0.
3)Случайные величины Х, Y, можно уменьшать (увеличивать) в α раз,
атакже вычитать или прибавлять к значениям X и Y одно и тоже число β –
это не приведет к изменению коэффициента корреляции .
При = ±1 случайные величины X и Y связаны линейной зависимо-
стью, т.е. Y X .
При = 0 линейная корреляционная связь отсутствует.
В практических расчетах коэффициент корреляции генеральной со-
вокупности обычно не известен. По результатам выборки может быть найде-
на его точечная оценка – выборочный коэффициент корреляции r, так как выборочная совокупность переменных X и Y случайна, то в отличие от пара-
метра , r – случайная величина. Оценкой коэффициента корреляции яв-
ляется выборочный коэффициент парной корреляции:
100
