4.3. Средние величины. Средняя арифметическая: свойства и методы расчета

Средняя является основной величиной в статистике, поскольку она характеризует центр распределения признака. Средние можно разделить на две группы:

- степенные (средняя арифметическая, геометрическая, гармоническая, квадратическая, кубическая);

- структурные (мода, медиана, квартиль, дециль, перцентиль).

Все виды степенных средних получаются на основе формулы:

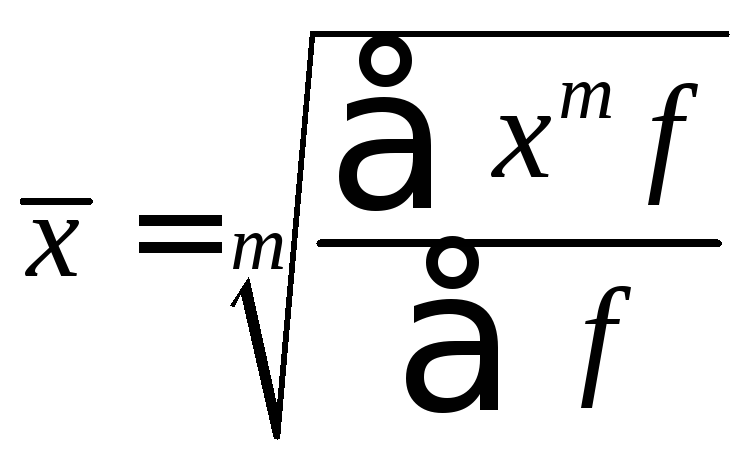, где x – значение признака, f – частота, вес, m – показатель степени.

Так, средняя арифметическая формируется при m=1:

.

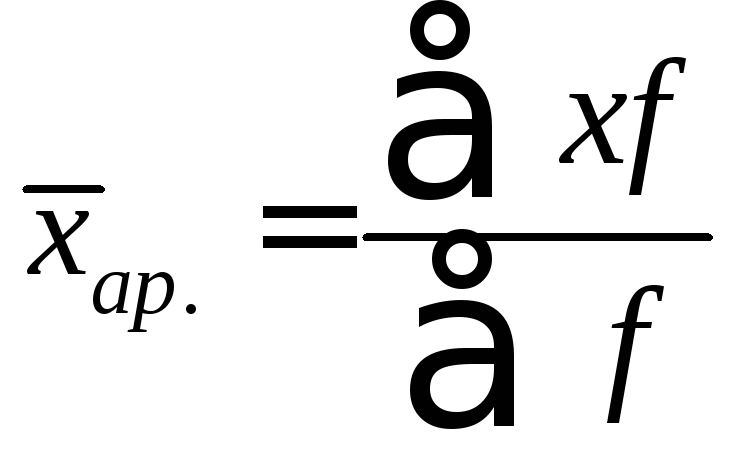Если ряд сгруппированный, то используется средняя арифметическая взвешенная.

Для не сгруппированного ряда используется средняя арифметическая простая: .

Среднее арифметическое обладает рядом свойств:

1. Средняя от постоянной величины равна ей самой: .

2. Произведение средней на сумму частот равно сумме произведений вариант на частоты: .

3. Изменение каждой варианты на одну и ту же величину изменяет среднюю на ту же величину: .

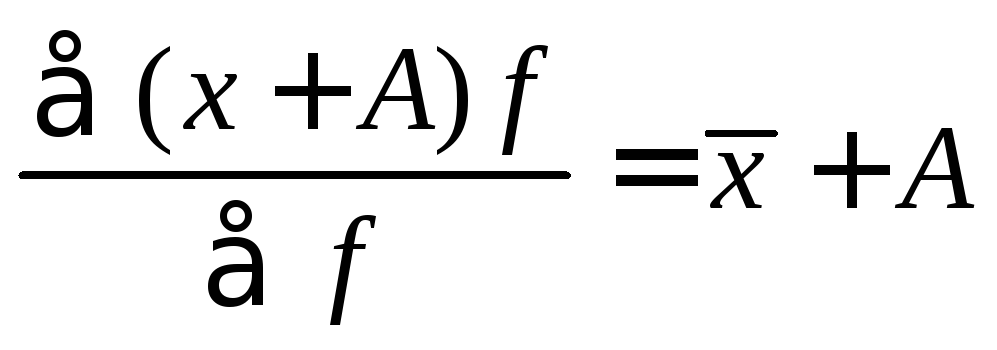4. Изменение всех вариант в одно и то же число раз во столько же раз изменяет среднюю: .

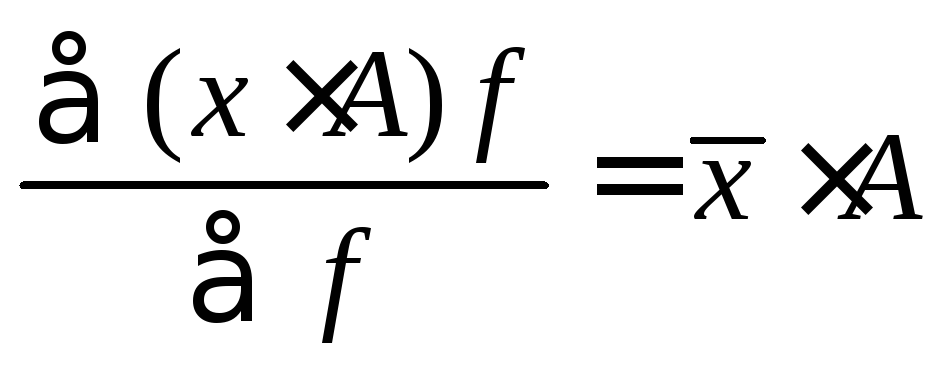5. Изменение всех весов (частот) в одно и то же число раз не изменяет значение средней: .

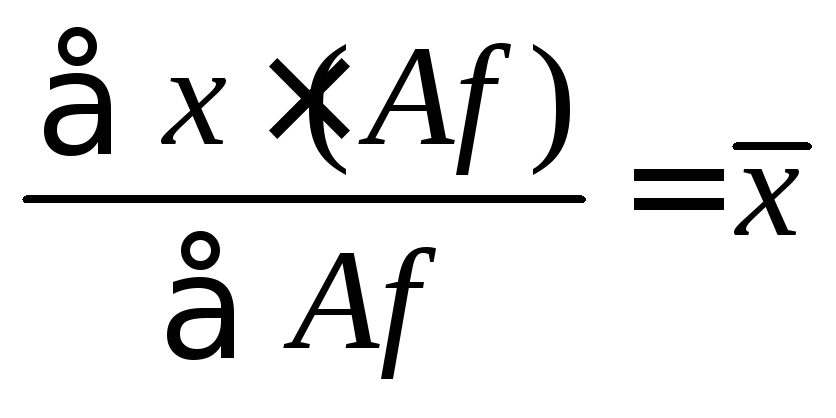6. Алгебраическая сумма отклонений всех вариант от средней равна 0: .

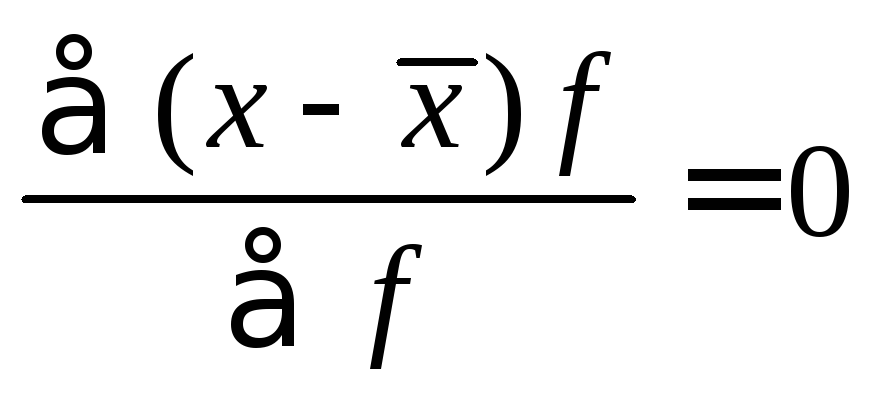7. Средняя суммы равна сумме средних: .

8. Сумма квадратов отклонений вариант от средней меньше, чем от любой другой величины: .

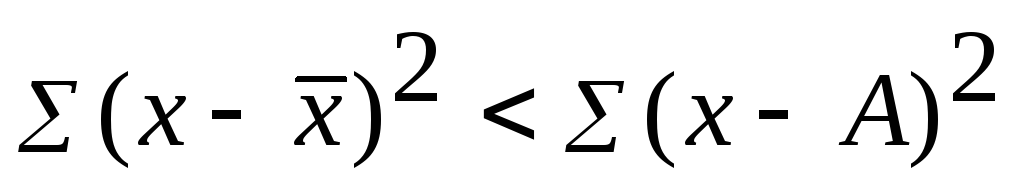Методы расчета средней величины

При расчете средней величины в числителе собирается все значение признака, а в знаменателе – общее количество единиц, обладающих данным признаком. Необходимо контролировать, чтобы и в числителе и в знаменателе были показатели, имеющие экономический смысл, и чтобы полученная средняя не выходила за границы минимального и максимального значений признака.

, где ФЗП – фонд заработной платы, – среднесписочная численность, – средняя заработная плата.

, где Q – количество товаров, услуг, – годовая выручка.

, где Р – рентабельность, П – прибыль.

, где– все значение признака,– количество единиц признака.

Пример 4.3

30 предприятий выполнили план на 80%, 20 предприятий на 102%, 50 предприятий на 98%. Определить средний процент выполнения плана по всем предприятиям.

Решение:

.

Пример 4.4

Рассчитать среднедушевой доход по приведенным данным (табл. 5).

Таблица 5

Группировка работников по доходам	Количество человек,	Средний доход по группам,руб.
до 5000	10	2500	2500
5000 - 10000	20	7500	15000
10000 - 15000	25	12500	312500
15000 -20000	30	17500	525000
20000 и выше	15	22500	337500
Итого:

Решение: .

Метод моментов (метод условного нуля)

, , гдеm₁ – момент первого порядка, h – величина интервала, А – варианта, соответствующая максимальной частоте.

Пример 4.5

По данным таблицы 6 рассчитать среднедушевой доход методом моментов.

Решение: Для нашего примера h=5000; А=17500

.

Таблица 6

Среднедушевой доход	Количество человек, f
до 5000	10	2500	– 3	– 30
5000 - 10000	20	7500	– 2	– 40
10000 - 15000	25	12500		– 25
15000 - 20000	30	17500		0
20000 и выше	15	22500	1	15
Итого		-	-