6.2. Парная регрессия

Парная регрессия отражает связь между двумя признаками – результативным и факторным. Аналитически эту связь можно представить уравнениями

- прямая,

- гипербола,

- парабола.

Для того чтобы определить, какая это связь, необходимо изучить само явление, то есть выявить: возможно ли монотонное возрастание или убывание функции, нет ли точек насыщения, перегиба, асимптот. После выбора возможного типа теоретической кривой определяются ее параметры с помощью метода наименьших квадратов «МНК»

Параметры выбранного типа теоретической кривой подбираются, исходя из условия, что сумма квадратов отклонений фактических значений результативного признака от теоретических будет минимальной. .

С этой целью на основе решения системы нормальных уравнений, определенных для каждого вида теоретической кривой, рассчитываются коэффициенты регрессии. Например, для линейной парной регрессии у=а₀+а₁х система нормальных уравнений имеет вид

,

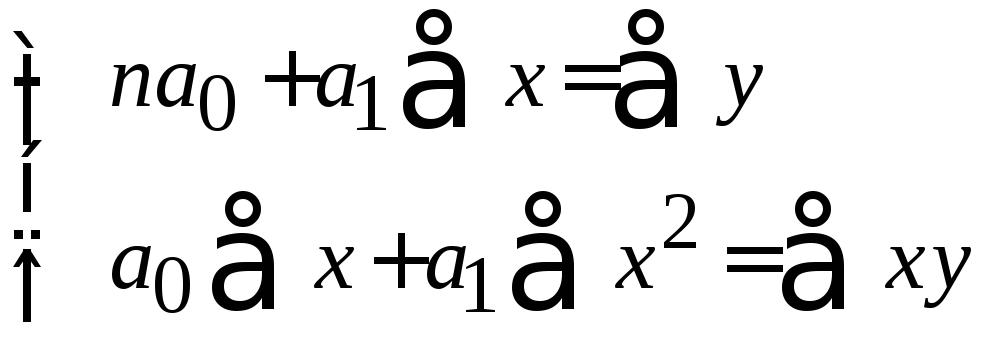где х и y – данные наблюдения.

Решение этой системы относительно а₀ и а₁ позволит определить коэффициенты регрессии в уравнении регрессии и составить уравнение теоретической кривой. Коэффициент при x показывает, на сколько своих единиц измерения изменяется результативный признак при изменении факторного признака на свою единицу измерения. Свободный член уравнения характеризует влияние всех прочих факторов кроме x.

Пример 6.1

Составить уравнение регрессии по данным таблицы 14.

Таблица 14

№ п/п	Прибыль у, тыс. руб.	Затраты на 1 руб. х, руб.
1	1200,00	0,96	0,92	1152,00	1869,19
2	2400,00	0,77	0,59	1848,00	1873,00
3	2480,00	0,77	0,59	1909,60	1873,00
4	1600,00	0,89	0,79	1424,00	1870,60
5	1750,00	0,82	0,67	1435,00	1872,00
6	1800,00	0,81	0,66	1458,00	1872,20
Итого:	11230,00	5,02	4,23	9226,60	11230,00

Решение

,

На основе уравнения регрессии можно сделать вывод, что с ростом затрат на единицу продукции на 1 рубль прибыль предприятия снижается на 20,1 тыс. руб.

6.3. Множественная (многофакторная) регрессия

Если определяется зависимость между двумя и более признаками, то говорят о наличии множественной регрессии.

Этапы исследования множественной регрессии:

- выбор формы связи;

- отбор факторных признаков;

- построение уравнения.

Теоретически уравнение множественной регрессии может быть представлено любой формой связи. Но одновременное влияние нескольких факторов, как правило, затушевывает конкретный вид зависимости.

Как правило, все виды нелинейных уравнений сводятся к линейным.

Количество факторов, включенных в модель, должно быть ограничено. С другой стороны оно должно быть достаточно, чтобы отразить влияние всех факторов.

В модель необходимо включать независимые или взаимосвязанные факторные признаки, при условии, что их влияние на результат признака будет больше их взаимного влияния друг на друга.

Из двух взаимосвязанных факторных признаков из модели исключается тот, чье влияние на результирующий признак будет меньше.

Система нормальных уравнений для трехфакторной модели:

Коэффициенты регрессии а₀, а₁, a₂ характеризуют влияние конкретных факторов: а₁ – показывает на сколько единиц измерений изменяется у при изменении х на свою единицу измерения.