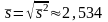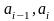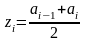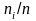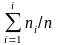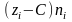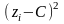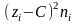Задача 1.7
Имеется выборка, полученная с помощью генератора случайных чисел
76,5 |
75,2 |
75,6 |
74,1 |
78,4 |
73 |
70,4 |
78,4 |
73,5 |
71,2 |
73,2 |
71,7 |
75,5 |
77 |
76,7 |
74,9 |
78,7 |
75,2 |
69,7 |
74,9 |
73,5 |
75,1 |
70,8 |
74,2 |
76,7 |
73,5 |
73,2 |
77,1 |
75,6 |
75,8 |
76 |
76,1 |
75,4 |
74,1 |
72,7 |
72,6 |
75,8 |
74,3 |
73,1 |
74,1 |
76,6 |
74,4 |
73,7 |
73,4 |
76,2 |
75,8 |
78,4 |
79,3 |
76,5 |
69,8 |
77,3 |
69,8 |
74,8 |
75,6 |
76,2 |
76,3 |
74,4 |
76 |
73 |
75 |
75,3 |
76,5 |
75,1 |
76,3 |
75,4 |
78,3 |
71,8 |
74,8 |
72,5 |
76,9 |
73,4 |
78,5 |
73,8 |
73,6 |
73,3 |
74 |
73,9 |
76 |
73,5 |
71,7 |
74,3 |
71,2 |
76,5 |
72,3 |
72 |
74,5 |
82 |
80,2 |
71,2 |
72,3 |
75,3 |
74,1 |
71,7 |
74,3 |
76,3 |
80,3 |
79,1 |
74,6 |
74,2 |
77,6 |
76,1 |
76 |
69,3 |
78 |
70 |
74,2 |
76,7 |
75,1 |
71,3 |
75,8 |
75,3 |
72,2 |
72,3 |
76,1 |
77,1 |
75,7 |
72,9 |
74,4 |
74,2 |
78,7 |
80,4 |
74 |
73,1 |
73,2 |
75,1 |
75,6 |
74,7 |
70,2 |
77,3 |
81,2 |
75,7 |
74,6 |
74,2 |
73,1 |
71,8 |
75,6 |
75,1 |
75 |
72,6 |
72,9 |
73,8 |
73,6 |
73,7 |
76,8 |
76,9 |
81,1 |
75,1 |
74,4 |
75,8 |
79,3 |
77,9 |
80 |
74,6 |
76,5 |
79,8 |
76,9 |
79,2 |
76,3 |
77,2 |
71,3 |
81,3 |
70,9 |
73,3 |
75,2 |
77 |
78,5 |
68,9 |
|
74,1 |
73,9 |
78,5 |
76,1 |
75,7 |
74,6 |
75,1 |
75,2 |
76,9 |
74,2 |
75,6 |
|
73,4 |
71,4 |
78,2 |
72,4 |
70,3 |
76,8 |
73,6 |
75,4 |
74,8 |
76,1 |
73,8 |
|
74 |
78,7 |
75,3 |
74 |
77,6 |
75,7 |
74,8 |
75,1 |
74,4 |
78,8 |
75,5 |
|
Требуется построить группированный статистический ряд и с его помощью найти приближенно выборочную функцию распределения и построить ее график; построить гистограмму; найти приближенно выборочные среднее и дисперсию.
Решение:
Объем выборки составляет 200 элементов.
Минимальный и максимальный элементы
выборки суть соответственно 68,9 и 82, т.е.
все элементы выборки находятся на
интервале (68,9;82). Пусть
,
.
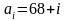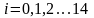Группированный статистический ряд
представим в виде таблицы 1 (при составлении
группированного ряда элементы выборки,
совпадающие с граничной точкой двух
интервалов, включаем в левый интервал)
Таблица 1
Интервал |
68- 69 |
69- 70 |
70- 71 |
71- 72 |
72- 73 |
73- 74 |
74- 75 |
75- 76 |
76- 77 |
77- 78 |
78- 79 |
79- 80 |
80- 81 |
81- 82 |
Частота |
1 |
5 |
5 |
12 |
13 |
29 |
33 |
40 |
28 |
9 |
12 |
6 |
3 |
4 |
Объединим интервалы, в которые попало «мало» элементов выборки: первых три и последних два. Далее найдем середины интервалов, частоты, относительные частоты и накопленные относительные частоты; результаты вычислений занесем в таблицу 2.
Теперь можно составить выборочную
функцию распределения
:
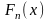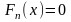при
;
если
,
,
то значение
есть число из
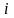-й
строки последнего столбца таблицы 2;
если
,
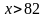то
.
График (приближенный) выборочной функции распределения и гистограмма представлены на рис.1 и рис.2 соответственно.
Таблица 2
Номер интервала i |
Границы интервала
|
Середина
|
Частота
|
Относит. частота
|
Накопл. отн. частота
|
1 |
-59, -57 |
-58 |
5 |
0,025 |
0,025 |
2 |
-57, -56 |
-56,5 |
5 |
0,025 |
0,05 |
3 |
-56, -55 |
-55,5 |
10 |
0,05 |
0,1 |
4 |
-55, -54 |
-54,5 |
26 |
0,13 |
0,23 |
5 |
-54, -53 |
-53,5 |
32 |
0,16 |
0,39 |
6 |
-53, -52 |
-52,5 |
27 |
0,135 |
0,525 |
7 |
-52, -51 |
-51,5 |
36 |
0,18 |
0,705 |
8 |
-51, -50 |
-50,5 |
27 |
0,135 |
0,84 |
9 |
-50, -49 |
-49,5 |
17 |
0,085 |
0,925 |
10 |
-49, -48 |
-48,5 |
10 |
0,05 |
0,975 |
11 |
-48, -46 |
-47 |
5 |
0,025 |
1 |
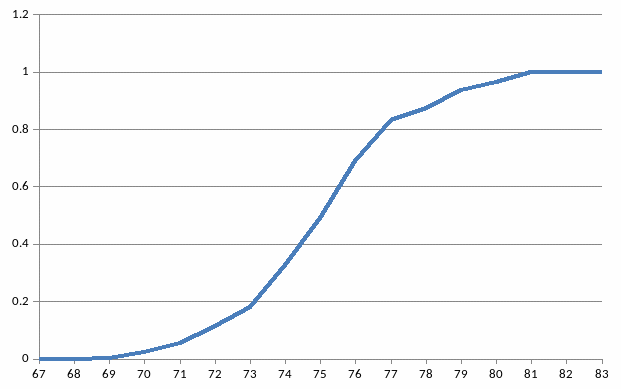
Рис.1 График выборочной функции
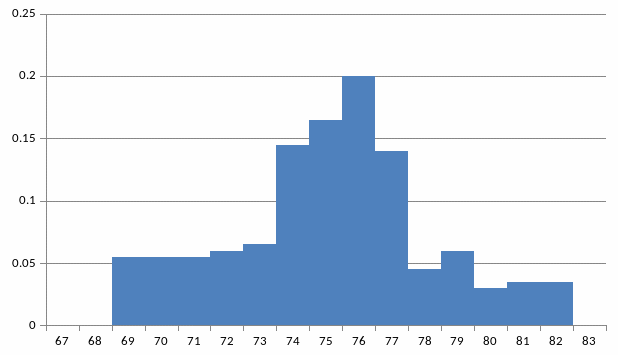
Рис.2 Гистограмма
При вычислении выборочных среднего,
дисперсии и среднего квадратического
отклонения в качестве «ложного нуля»
возьмем середину интервала с максимальным
значением частоты, округлять до ближайшего
целого не будем
.
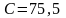Формулы для нахождения среднего, дисперсии и среднего квадратического:
;
;
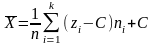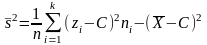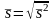
Вычисление оформляем в виде таблицы 3
Таблица 3
|
|
|
|
|
|
69,5 |
11 |
-6 |
-66 |
36 |
396 |
71,5 |
12 |
-4 |
-48 |
16 |
192 |
72,5 |
13 |
-3 |
-39 |
9 |
117 |
73,5 |
29 |
-2 |
-58 |
4 |
116 |
74,5 |
33 |
-1 |
-33 |
1 |
33 |
75,5 |
40 |
0 |
0 |
0 |
0 |
76,5 |
28 |
1 |
28 |
1 |
28 |
77,5 |
9 |
2 |
18 |
4 |
36 |
78,5 |
12 |
3 |
36 |
9 |
108 |
79,5 |
6 |
4 |
24 |
16 |
96 |
81 |
7 |
5,5 |
38,5 |
30,25 |
211,75 |
|
200 |
- |
-99,5 |
- |
1333,75 |
Отсюда:
;
;
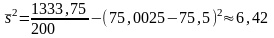