6.4. Параметрические методы изучения связи

Для определения тесноты связей используются следующие показатели: линейный коэффициент корреляции, эмпирическое и теоретическое корреляционное отношение, множественный коэффициент корреляции, частные коэффициенты корреляции.

Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя признаками при наличии между ними линейной зависимости.

Линейный коэффициент корреляции обозначается r и рассчитывается:

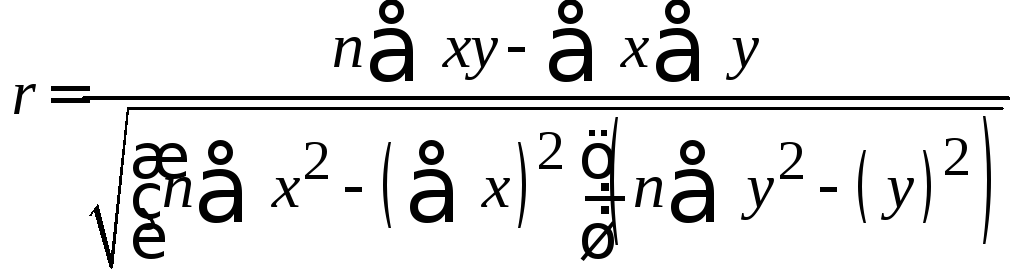
х, у находят из наблюдений, n – количество наблюдений.

r изменяется от -1 до +1, то есть

При связь отсутствует, присвязь функциональная (нет различных случайных факторов), присвязь обратная, при– прямая.

Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость:

Эмпирическое отношение: ,

где – общая величина дисперсии эмпирических значений признака;

–межгрупповая дисперсия, которая характеризует формирование группового признака.

Теоретическое отношение: .

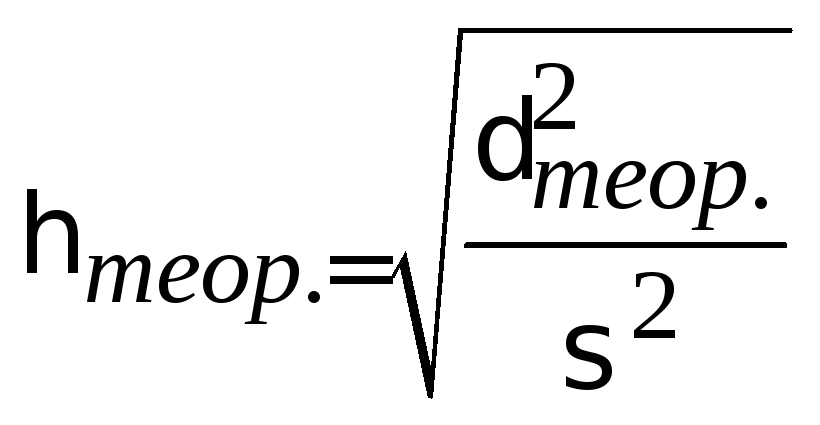Корреляционное отношение изменяется от 0 до 1.

Множественный коэффициент корреляции R рассчитывается при наличии связи между результативным признаком и несколькими факторными. Этот коэффициент позволяет оценить тесноту связи факторов, включенных в модель, и результативного признака .

R изменяется от 0 до 1, при этом, чем ближе значение к 1, тем больше взаимосвязь.

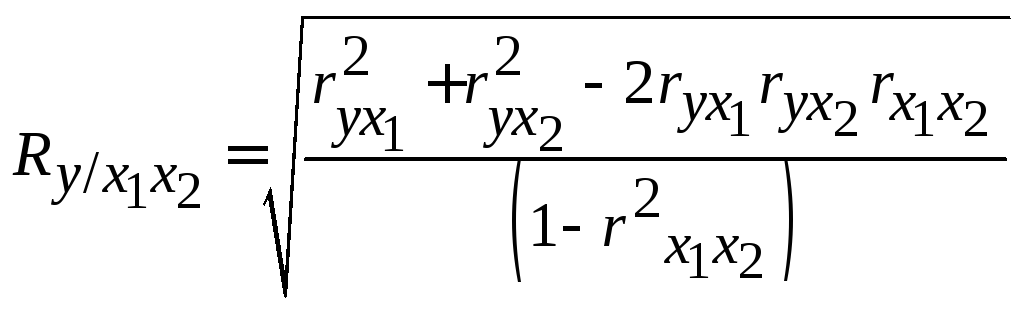
Частные коэффициенты корреляции характеризуют тесноту связи при фиксированном значении других факторных признаков, т.е. связь в чистом виде.

Частные коэффициенты корреляции для трехфакторной модели имеют следующий вид:

.

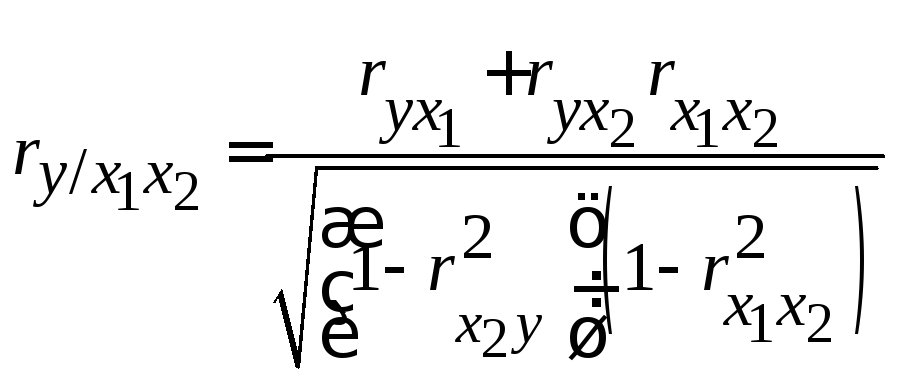
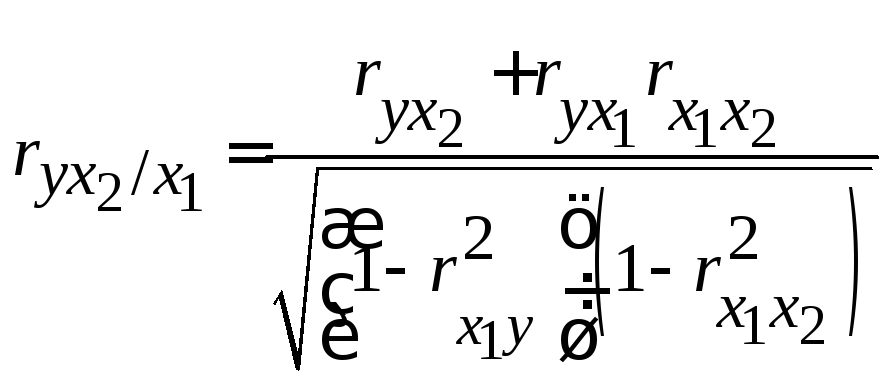Частные коэффициенты изменяются от до.

6.5. Принятие решений на основе уравнения регрессии

Полученные регрессионные модели позволяют использовать их для принятия обоснованного управленческого решения, но при этом следует иметь в виду, что полученная закономерность верна только для тех условий, для которых она была рассчитана или для подобных условий.

С целью расширения возможности анализа используют коэффициенты эластичности, которые показывают, на сколько процентов в среднем изменяется значение результативного признака при изменении факторного на 1%.

В уравнении множественной регрессии используют частные коэффициенты детерминации

Коэффициент эластичности связан коэффициентом регрессии: , где- парный коэффициент корреляции между результативным и факторным признаком,- стандартизованный коэффициент детерминации.

Стандартизованные коэффициенты детерминации связаны с коэффициентом регрессии: .

Стандартизованные коэффициенты детерминации показывают, на сколько средних квадратических отклонений изменяется результативный признак при изменении факторного признака на одно среднеквадратическое отклонение.

Коэффициенты эластичности и стандартизованные коэффициенты позволяют сопоставить варианты достижения одного и того же результата.

Контрольные вопросы к теме 6

1.Сравните характеристики функциональной и корреляционной связей

2.Перечислите показатели тесноты связи между признаками в парной корреляции

3.Приведите показатели тесноты связи между признаками во множественной корреляции.

4.О чем говорят коэффициенты регрессии в уравнении регрессии?

5.Что характеризуют коэффициенты детерминации?