14. Симплекс-таблицы
Алгоритм метода Жордана-Гаусса
Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:
1. Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
2.Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
3. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
4. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
5. Далее заново переходят к пункту 1
15. Графическое решение двумерных задач линейного программирования
Графическое решение двумерных задач линейного программирования основан на геометрической интерпретации ЗЛП и применяется в основном при решении задач двумерного пространства и только некоторой. задачи трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств.
Пусть ЗЛП задана в двумерном пространстве, то есть ограничения содержат 2 переменные.
Найти
минимальное значение функции (1)
z=c1x1+c2x2
при ограничениях (2)
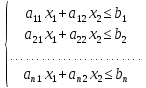и
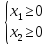(3)
Допустим, что система (2) при условии (3) совместна. Каждое из неравенств из системы (2) и (3) опред. полуплоскость с граничными прямыми.
(i=1,2,…,n)
x1=0
x2=0
Линейная
функция(1) при фиксированных значениях
z
является уравнением прямой линии
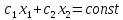
Построим
многоугольник. Решение системы
ограниченной (2) и график линейной функции
(1) при z=0.
Тогда поставленной ЗЛП можно дать
следующую интерпретацию. Найти точку
многоуг. Решений, в которой прямая
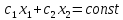опорная иz
достигает min.
Значения z
уменьшается в направлении вектора
N=(-c1,
-c2)
поэтому z=0
передвигаем параллельно самой себе в
направлении N.
Координаты E(x1,x2) находим из системы уравнений прямых DE и EF. Если те мноуг. Решение представляет собой неограниченную многоугольную область, то возможно 2 случая.
Случай
1. Прямую
,
передвигаем в направлении вектораN
или противоположно ему, постоянно
пересекает многоуг. Решений и ни в какой
точке не является опорной к нему. В этом
случае линейная функция не ограничена
в многоуг. Решений как сверху так и с
низу.
Случай 2. Прямая передвигаясь становится опорной относительно многоугольных решений. Тогда в зависимости от вида области линейной функции может быть ограниченной сверху и не ограничена снизу, либо ограничена как сверху так и снизу.
16. Динамическое программирование
Математической основой динамического программирования является принцип Белмона. Каким бы ни было текущее состояние и каким бы способом система не пришла в это состояние любое последующее решение должно обеспечивать оптимальное поведение на всем этапе развития системы.
Математический принцип может быть выражен следующим соотношением: fn-l(Sl)=optimum(fn-(l+1)(Sl)+Rl+1(Sl,Ul+1))
S- состояние системы на l шаге. U – вектор возможных допустимых управленческих решений. f – достигнутый эффект, за все пройденный шаги. R – достигнутый эффект на следующем шаге. n – полное количество шагов развития системы.
Наиболее часто анализ развития системы выполняется с конца т.к. после достижения системы окончательного состояния можно получить достигнутый эффект =0, а затем просматривая в обратном порядке все возможные состояния и эффекты на очередном шаге можно выбрать наиболее оптимальное управленческое решение.
Пример. задача о кредитовании.