11. Основная задача линейного программирования.

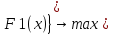min)

При условии, что на эти переменные наложить след. условия:

G_i(x)>=b_i

G_k(x)<=B_k ограничения

G_m(x)=c_m

X_i>=0 не отрицательность

F(x) целевая функция

Решение данных задач оптимизации приводится в рамках раздела математики в матем. программирование.

В задачах матем. программирования выделяют:

- линейное программирование – когда все функции g и f явл. линейными относительно х.

- не линейного программирования – когда функции не линейные

- динамическое программирование – многошаговые задачи

- теория систем массового обслуживания

- теория игр

- статистическое программирование

- сетевое планирование

- теория расписаний и т.д.

12. Геометрическая интерпретация

Г. М. решений задач Л. П. отличается от хорошей наглядностью. Выделяют два случая Г. М.: с 2-мя переменными и со многими.

1) С 2-мя переменными:

1. Строится ОДЗ: для этого строятся граничные линии из системы ограничений.

2. Строится направляющий вектор 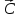. Координаты которого – коэффициенты переменных Ц.Ф.

3. Строится Ц.Ф., т.е. Выражение Ц.Ф. приравнивается к нулю.

4. В данном случае – градиент функции, т.е. Ц.Ф. возрастает в направлении вектора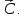Поэтому в направлении, двигаясь до тех пор, линия уровня, параллельная Ц.Ф., не коснется ОДЗ в 1-й раз. Эта точка минимум. А когда коснется в последний раз, то максимум.

Координаты точек (мин)мак определяются либо путем опускания перпендикуляра на координаты оси, либо решением системы уравнений, соответствующих прямых, на пересечении которых находится точка экстремума.

5. Находим значение функции в точках экстремума.

2) Со многими переменными:

Имеет место, если

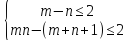
n - число неизвестных в Ц.Ф.

m – количество линейно-независимых уравнений в С. О.

Если это выполняется:

1. Выбираем в качестве свободных две переменные.

2. Выражаем все остальные переменные через, выбранные свободные, т.е. решаем С.О. заданной задачи.

3. Выражаем Ц.Ф. через свободные переменные.

4. Полученную двухмерную задачу решаем Г.М. для 2-ух переменных.

5. Найдя координаты оптимального решения двухмерной задачи, подставляем их в ограничения исходной задачи и определяем остальные координаты оптимального решения.

13. Симплекс-метод

Пусть дана задача линейного программирования в канонической форме. Т.е.

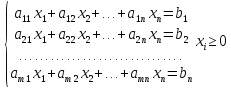
Задачу линейного програмирования записывают в форме модифицированной Жардановой таблице(симплексная таблица)

Для начала необходимо выбрать начальное опорное решение. Для этого Жардановыми исключениями необходимо переменные из заглавной строки перенести в заглавный столбец вместо нулей.

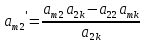
Коэффициенты новой симплексной таблицы находятся по следующему правилу: разрешающий элемент заменяется обратной величиной.

1) Разрешимым называется элемент стоящий на пересечении столбца с переносимой переменной и строки в которую эта переменная переносится.

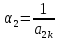
2) остальные элементы разрешающей строки делятся на разрешающий элемент

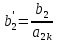и т.д.

3) Остальные элементы разрешающего столбца делятся на разрешающий элемент и меняют знак на противоположный

4) прочие элементы таблицы вычисляются по правилу прямоугольника

Выполнив достаточное количество Жардановых исключений, исключить все нули в заглавном столбце тогда начальное опорное решение имеет вид: переменные стоящие в заглавном столбце равны свободным членам; переменные оставшиеся в заглавной строке равны 0.

Для того чтобы в столбце свободных членов не появились отрицательные элементы, необходимо придерживаться след. Правилам:

1. Разрешающим может быть выбран любой столбец содержащий хотя бы один положительный элемент.

2. Разрешающий выбирается строка соответствующая минимальному симплексному отношению.

Симплексным отношением называется отношение свободных членов к соответствующим положительным элементам разрешающего столбца.

Замечание.

1. Разрешающие столбцы будут иметь нули в верхней (заглавной) строке и их можно вычеркивать

2. Можно вычеркивать строки из нулей

3. Если в процессе исключений встретится ноль-строка, все элементы которой нули , кроме свободного члена, то система ограничений не имеет решения

4. Если встретится ноль-строка в которой кроме свободного члена других положительных элементов нет, то система не имеет неотрицательных решений

На следующих этапах необходимо проводить оптимизацию найденного опорного начального решения.

Правило оптимизации опорного плана(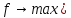

1. Если в f-строке нет отрицательных элементов, кроме свободного члена, то план оптимален

2. Если в f-строке нет также и нулевых элементов, то оптимальный план единственен, если же среди элементов есть хотя бы один нулевой , то оптимальных планов бесконечно много

3. Если в f-строке имеется отрицательный элемент, а в соответствующем ему столбце нет положительных, то целевая функция в допустимой области не ограничена и задача не разрешима.

4. Если в f-строке имеется хотя бы один отрицательный элемент, а в каждом столбце с таким элементом есть хотя бы один положительный, то можно перейти к новому опорному плану более близкому к оптимальному

5. Для наилучшего выбора разрешающего элемента за разрешающий столбец необходимо выбирать столбец с наибольше по модулю отрицательным элементам в f-строке

6. Разрешающей строкой как и раньше выбирается строка с наименьшим симплексным отношением

7. После каждого шага Жардановых исключений найденное решение анализируется на оптимальность.