13.4. Интеграл фурье. Преобразования фурье

Теорема 2.Если- 1) абсолютно интегрируемая нафункция, т.е. удовлетворяющая условию; 2) кусочно-гладкая на каждом конечном отрезке, то ееинтеграл Фурье

(4.1)

где (4.2)

(4.3)

равен в каждой точке непрерывностиив каждой точке разрыва.

Если - четная, то

, (4.4)

Если - нечетная, то

; (4.5)

Для представления интегралом Фурье функции, заданной лишь в промежутке и продолженной четным образом на, используем формулы (4.4), а продолженной нечетным образом – формулы (4.5).

Если и, найденные по формулам (4.4), подставить в (4.1), то получим двойной интеграл Фурье для четной функции:

Положив

, (4.6)

получим

(4.7)

Равенство (4.6) называется косинус – преобразованием , а (4.7) – косинус – преобразованием.

Аналогично, если - нечетная, то

(4.8)

называется синус - преобразованием , а

(4.9)

называется синус - преобразованием .

Комплексная формаинтеграла Фурье имеет вид

(4.10)

где

(4.11)

Связь между и:

Функция называетсяспектральной характеристикойфункции.называетсяспектромфункции.

Функция называется также преобразованием Фурье функции, в этом случае ее обычно обозначают

Пример.Представить интегралом Фурье функцию

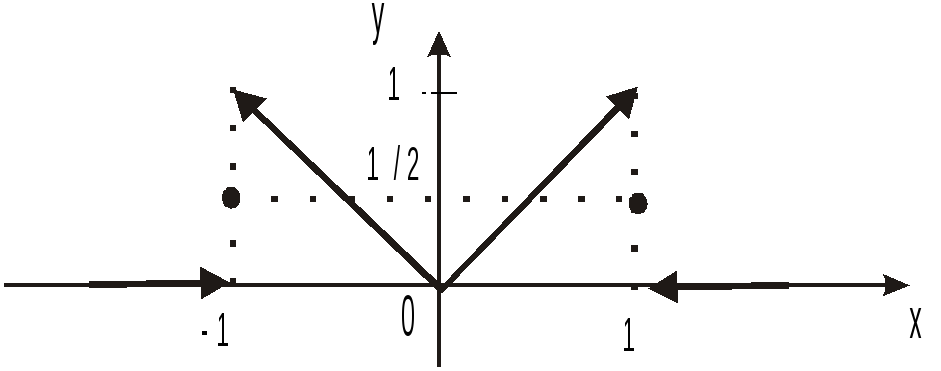
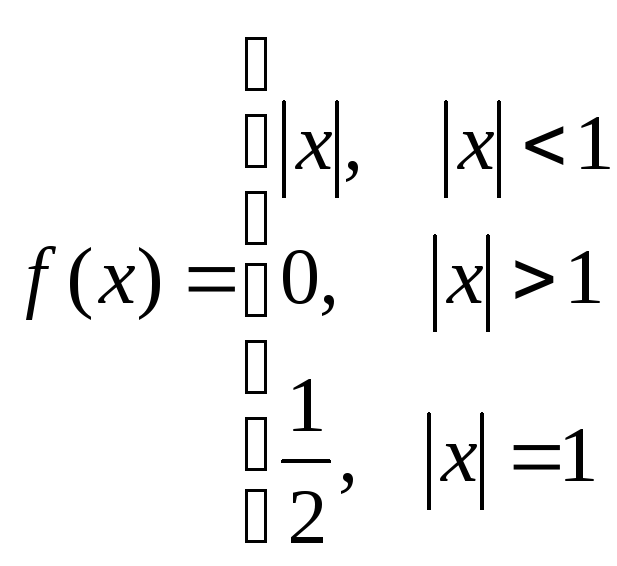
 Построим график данной функции.

Рис.4.

Данная функция 1) имеет 2 точки разрыва Iрода; 2) абсолютно интегрируема на всей осиOx: . 3) данная функция – четная, поэтому на основании (4.4) .

Данная функция является непрерывной в интервалах ; (-1,1);, кроме того, в точках разрыва среднее арифметическое односторонних пределов функции совпадает со значением ее в этих точках, поэтому можно записать интеграл Фурье.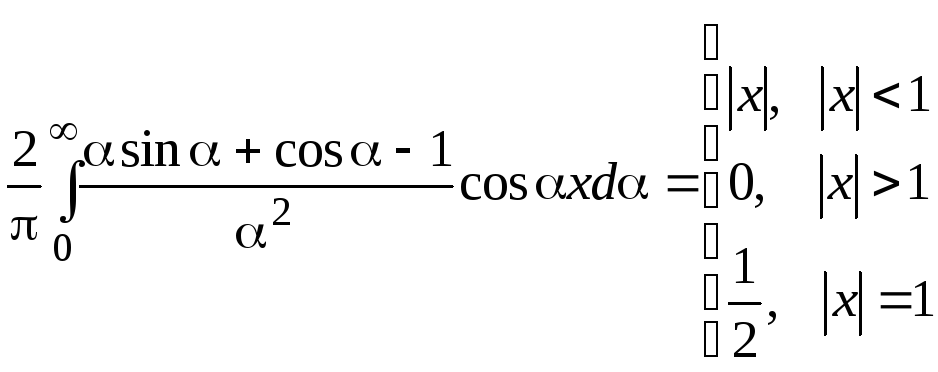

Пример.Показать, что спектральной характеристикой функции

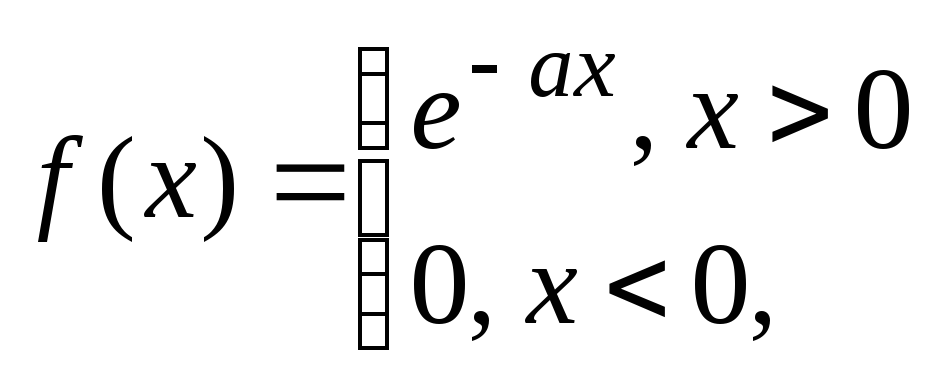, является функция. Построить график спектра.

 Построим график данной функции.

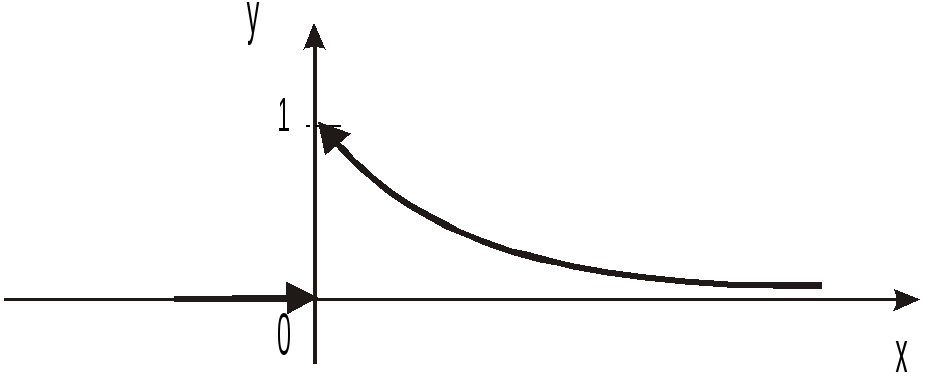Рис.5.

Найдем по формуле (4.11) .

Спектр - это..

Построим график .

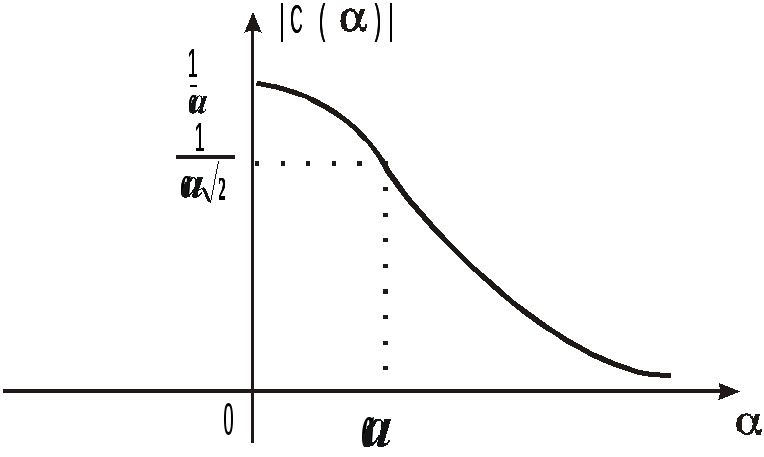Рис. 6. 

Задачи для самостоятельного решения

В задачах № 14 – 17 представить интегралом Фурье следующие функции:

14. 15.

16. 17.

18. Функцию, представить интегралом Фурье, продолжая ее 1) четным образом, 2) нечетным образом на промежуток. Найти значения интегралови.

19.Используя результат задачи 18, представить интегралами Фурье функции

1) ; 2) .

20.Написать интеграл Фурье в комплексной форме для функций

1), 2).

2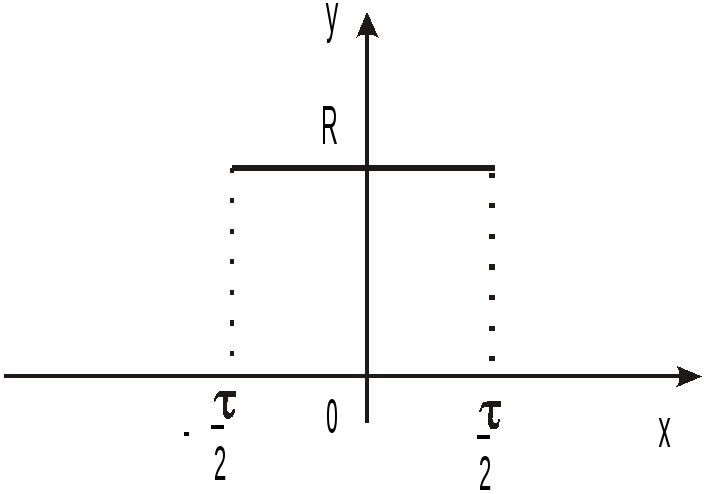1.Вычислить спектр прямоугольного импульса высотойhи длительностьюи построить график спектра.

Рис. 7.

22.Записать преобразование Фурье для следующих функций:

1) ; 2).