Задачи для самостоятельного решения
Найти сумму ряда в № 25-31.
25. 26.
27. 28.29.
30.
31.
Исходя из соотношения
,
найти сумму ряда: а)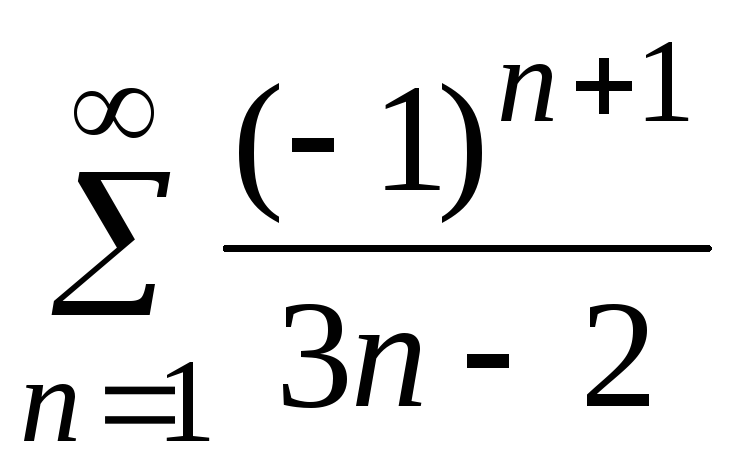
;
б)
.32.
Доказать, что ряд
сходится равномерно на
,
но что его нельзя дифференцировать ни
в какой точке этого интервала.
12.5. Ряды тейлора и маклорена. Разложение функций в ряд
ТЕЙЛОРА И МАКЛОРЕНА
Пусть
функция
имеет в т.
и некоторой ее окрестности производные
любого порядка. Ряд
(5.1)
называется
рядом Тейлора
для функции f(x).
Если же для всех значений x
из некоторой окрестности т.
ряд сходится и имеет суммойf(x),
т.е.
,
то
f(x)
называется разложимой
в ряд Тейлора
в окрестности т.
( или по степеням
).
Еслиx
= 0, то ряд Тейлора имеет вид
и называется рядом Маклорена.
Теорема
8. Для того,
чтобы функция
была разложима в ряд Тейлора в окрестности
т.
,
необходимо и достаточно, чтобы
.
-
остаточный член формулы Тейлора.
Записанный в форме Лагранжа, он имеет
вид:
,
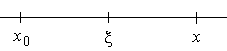
Теорема
9. Если
имеет в некотором промежутке, содержащем
т.
,
производные всех порядков, для которых
,
то
при
и значит
разложима в этом промежутке в ряд
Тейлора.
То же самое в символической записи :
.
При
разложении
в ряд Тейлора применяют следующие
приемы:
1)
Непосредственное разложение
в
ряд Тэйлора, которое состоит из трех
этапов:a)формально
составляют ряд Тэйлора, для чего находят
для
любыхn,
вычисляют
и подставляют найденные значения в
(5.1);b)
находят область сходимости ряда (5.1); c)
выясняют, для каких значений x
из области сходимости ряда
,
т.е. для какихx
имеет место равенство:
.
2) Использование готовых разложений:
.
Пример.
Разложить
в ряд Тейлора в окрестности т.x
= 2.
Решим эту задачу двумя способами.
I
способ. Используем непосредственное
разложение функции в ряд Тейлора:1)
;
……………………………………………………
……………………………………………………
Вычислим найденные производные в т. x = 2:
…,
,…
Составим формально ряд Тейлора:
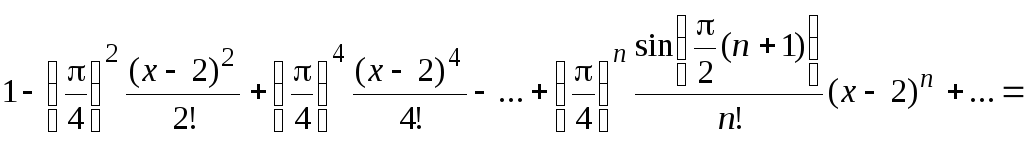
(5.2)
б) Найдем область сходимости ряда (5.2), используя признак Даламбера:
Этот
результат будет справедлив при любых
x,
следовательно, ряд (5.2) сходится на всей
числовой оси:
.
в)
Докажем, что при всех x
ряд (5.2) сходится к
,
для чего достаточно показать, что
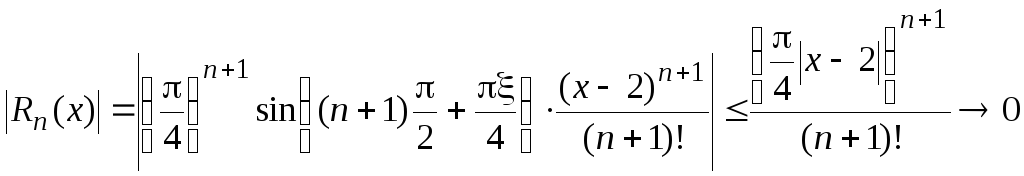при
:
при
.
Как результат решения задачи можем
записать:
,
.
II
способ. Разложим
в ряд Тейлора в окрестности т.x
= 2, используя готовое разложение.
Преобразуем
следующим образом:
.
В ряд Маклорена для cosx
(5.3)
справа
и слева вместо x
подставим
,
получим:
;
(5.4)
(т.к.
в (5/3)
При разложении функции в ряд часто используют почленное дифференцирование и интегрирование рядов.
Пример.
Разложить в ряд Маклорена
.
Предварительно
разложим в ряд Маклорена функцию
,
для чего в разложении
заменимx
на
.
.
Поэтому
(получившийся ряд сходится и в граничных
точках).
Задачи для самостоятельного решения
Следующие функции разложить в ряд Маклорена
33.
;
34.
35.
;
36.
;
37.
;
38.
;
39.
;
40.
.
41.
;
42.
;
43.
.
44.
;
45.
;
46.
;
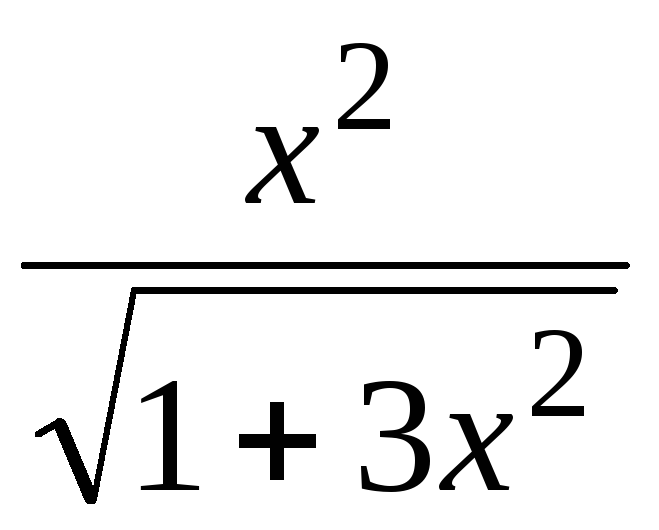47.
.
Следующие
функции разложить в ряд Тейлора в
окрестности т.
.
Указать область сходимости найденного ряда к своей сумме.
48.
.
49.
.
50.
.
51.
.
52.
.
53.
.
54.
.
55.
.
56.
.
12.6. ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ
Если некоторое число S разложено в ряд
(6.1)
и
,
то поправка на отбрасывание всех остальных членов выразится остатком
.
Как произвести оценку погрешности?
1)Если
ряд (6.1) – знакочередующийся, то остаток
имеет знак своего первого члена
и
.
2) Если ряд (6.1) – знакоположительный, то остаток оценивают либо с помощью остаточного члена формулы Тейлора, либо пытаются найти легко суммируемый тоже знакоположительный ряд, члены которого были бы больше членов интересующего нас остатка и оценивают остаток ряда (6.1) суммой найденного ряда.
Обычно ищут десятичное приближение числа S, в то время как члены ряда
могут и не быть десятичными дробями. При обращении их в десятичную дробь возникает новая погрешность, которую тоже нужно учесть.
Пример.
Какова величина допущенной ошибки, если
приближенно положить
?
Ошибка будет суммой знакоположительного ряда
.
(6.2)
а) Оценим эту ошибку, заменив члены ряда (6.2) членами геометрической прогрессии, которые будут больше членов ряда (6.2)
.
б) оценим эту же ошибку с помощью остаточного члена формулы Маклорена
.
В нашем случае
.
Пример.
Вычислить
с точностью до 0,001 (предполагаем, что
).
.
Проинтегрируем полученное разложение на [0, 2]:
(6.3)
Получили
знакочередующийся ряд. Если для вычисления
интеграла
взять 4 члена ряда (6.3), то ошибка
,
которая получается за счет отбрасывания
членов ряда, начиная с пятого, не будет
превосходить первого из отброшенных
членов, т.е.
.
Вычисления нужно вести с 4 знаками после
запятой, тогда ошибка
,
которая получается при обращенииII,
III,
и IV
членов ряда (6.3) в десятичные дроби будет
меньше
.
Общая ошибка
.
.
Результат округлен доIII
знака после запятой.
Пример.
Найти общее решение дифференциального
уравнения
в виде степенного ряда.
Т.к. x = 0 не является особой точкой для данного дифференциального уравнения, то решение его можно искать в виде ряда
(6.4)
Продифференцируем ряд (6.4) дважды:
.
(6.5)
Подставим
в уравнение вместо
и
соответственно ряды (6.4) и (6.5):
или
.
Приравнивая
коэффициенты при всех степенях x
к нулю, получим:
.
,
и т.д.
Пример. Применяя метод последовательных дифференцирований, найти 5 членов разложения в ряд решения дифференциального уравнения
при
начальных условиях
.
Точка x = 0 не является особой точкой данного дифференциального уравнения, поэтому решение можно искать в виде:
(6.6)
(разложение
в окрестности x
= 0!). Здесь
.
Из
уравнения
.
Из
уравнения
,
,
.
Подставим
в (6.6)
:
или
Задачи для самостоятельного решения
57.
Вычислить приближенное значение
,
взяв 3 члена разложения в ряд Маклорена
функции
,
оценить погрешность.
58.
Вычислить приближенное значение
,
взяв 3 члена разложения в ряд Маклорена
функции
,
оценить погрешность.
Вычислить приближенно с указанной степенью точности .