Задачи для самостоятельного решения

Найти сумму ряда, исходя из определения.

1. 2. 3.

Доказать расходимость рядов с помощью необходимого признака.

4. 5. 6.

Решить вопрос о сходимости рядов с помощью признаков сравнения.

7. 8.9.

10. 11.12.

13. 14.

Исследовать сходимость рядов с помощью признака Даламбера.

15. 16.17.

18. 19.20.

Исследовать сходимость рядов с помощью признака Коши (радикального).

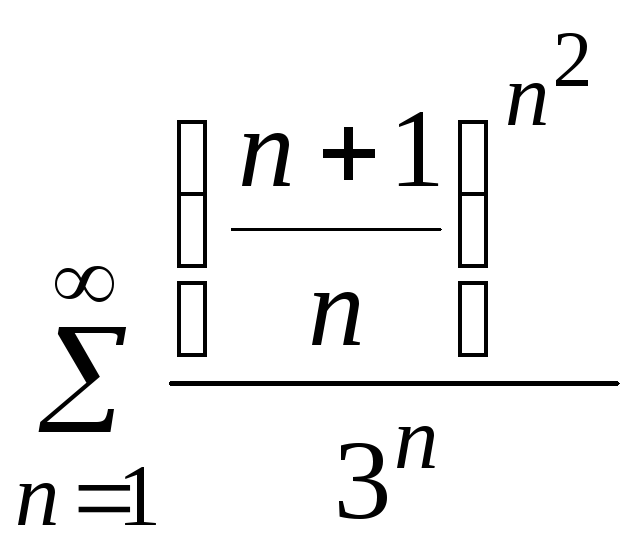21. 22.23.

Исследовать сходимость рядов с помощью интегрального признака Коши.

24. 25.

Выяснить, какие из рядов сходятся, какие расходятся.

26. 27.28.

29. 30.

31. 32.33.

34. 35. Доказать, что .

Исследовать сходимость следующих рядов. В случае сходимости исследовать, как ряды сходятся : абсолютно или условно.

36. 37.38.

39. 40.41.

42. 43.44.

45.

46. Показать, что если ряды исходятся, то и рядабсолютно сходится.

47. Показать, что если ряд абсолютно сходится, то и рядтоже абсолютно сходится.

48. Дан ряд Оценить ошибку, допускаемую при замене суммы этого ряда суммой его первых четырех членов. Суммой первых пяти членов. Что можно сказать о знаке этих ошибок?

49. Сколько нужно взять членов ряда , чтобы вычислить его сумму с точностью до 0,01? до 0,001?

Ответы к задачам главы 11

1)	2)	3)	7)Расходится	8)Расходится
9)Сходится	10)Сходится	11)Сходится	12)Сходится	13)Сходится
14)Сходится	15)Сходится	16)Сходится	17)Сходится	18)Сходится
19)Сходится	20)Расходится	21)Сходится	22)Сходится	23)Расходится
24)Расходится	25)Сходится	26)Сходится	27)Расходится	28)Сходится
29)Расходится	30)Расходится	31)Сходится	32)Расходится	33)Сходится

34)Сходится36)Сходится абсолютно37)Сходится условно38)Сходится абсолютно

39)Сходится абсолютно40)Расходится41)Сходится условно42) Сходится условно

43)Расходится44)Сходится абсолютно45)Сходится абсолютно

48)а) ошибка по модулю меньше, ошибка отрицательная.

49)а) 99членов; б) 999 членов.

Г Л А В А 12

Фунциональные ряды

12.1. Функциональные ряды. Основные понятия

Ряд

, (1.1)

членами которого являются функции от x, определенные на множествеD, называетсяфункциональным рядом. Если числовой рядсходится, где, тоназываетсяточкой сходимости ряда (1.1). Множество всех точек сходимости ряда (1.1) называетсяобластью сходимостиряда (1.1). Если существует, где,, то говорят, что ряд (1.1) сходится на множествеXкS(x).S(x) называетсясуммой ряда(1.1). На языке “” это можно записать так:

.

Для нахождения области сходимости ряда (1.1) можно использовать эталонные ряды и достаточные признаки сходимости числовых рядов.

Пример. Найти область сходимости ряда.

 Данный ряд представляет собой обобщенный гармонический ряд, который сходится при и расходится при. Областью сходимости ряда является интервал.

Пример.Найти область сходимости ряда.

 Данный ряд является геометрической прогрессией, которая сходится, если .. Область сходимости ряда – интервал.

Пример.Найти область сходимости ряда

(a)

 Для нахождения области сходимости данного ряда используем признак Даламбера, который применим лишь к рядам с положительными членами. Составим ряд из абсолютных величин членов данного ряда:

(б)

и к нему применим признак Даламбера (теорема 11.4). . Ряд (б) будет сходиться, если. Тогда ряд (а) будет сходиться, и притом абсолютно в интервале (-4, 0). Приряд (а) расходится, как не удовлетворяющий необходимому признаку сходимости (следствие из теоремы (11.1)). Если, то ответа о сходимости ряда признак Даламбера не дает и прииряд нужно исследовать особо. Прииз ряда (а) получим числовой ряд, который сходится (ряд Лейбница) (см. задачу раздела (11.6)). Прииз ряда (а) получим- гармонический ряд, который расходится (раздел 11.2). Итак, областью сходимости ряда (а) будет промежуток [-4,0).