
- •Глава 1. Действительные функции одного переменного
- •1.1. Основные понятия и определения
- •Задачи для самостоятельного решения
- •1.2. Некоторые типы функций
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •1.3. Обратная функция
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 1:
- •Глава 2. Предел функции
- •2.1. Предел функции. Основные понятия
- •2.2. Предел дробно-рациональной функции. Иррациональные выражения.
- •Задачи для самостоятельного решения
- •2.3. Бесконечно малые величины. Первый замечательный предел.
- •Задачи для самостоятельного решения
- •2.4. Второй замечательный предел
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 2:
- •Глава 3. Непрерывность функции
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 3:
- •Глава4. Дифференциальное исчисление функции одной переменной
- •4.1. Производная. Дифференцирование явно заданных функций
- •Производная сложной функции. Пусть функция имеет производную в точке, а функцияимеет производную в точке. Тогда сложная функцияимеет производную в точкеи справедливо равенство;.
- •Задачи для самостоятельного решения
- •4.5. Дифференциал
- •Необходимым и достаточным условием дифференцируемости функции в точке является существование у функции производной в данной точке, при этом справедливо равенство .
- •Дифференциалом второго порядка функции называется первый дифференциал первого дифференциала, то естьи он обозначаетсяили.
- •Задачи для самостоятельного решения
- •4.8. Формула Тейлора
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 4:
- •Глава 5. Исследование функций с помощью производных
- •5.1. Возрастание и убывание функций
- •5.2. Точки экстремума функций.
- •Задачи для самостоятельного решения
- •5.3. Исследование функций на выпуклость и вогнутость. Точки перегиба функций.
- •Задачи для самостоятельного решения
- •5.4. Асимптоты графика функции
- •Задачи для самостоятельного решения
- •5.5 Общая схема исследования функций.
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 5:
Задачи для самостоятельного решения
Найти пределы, используя правило Лопиталя.
82.![]() .
83.
.
83.![]() .
84.
.
84.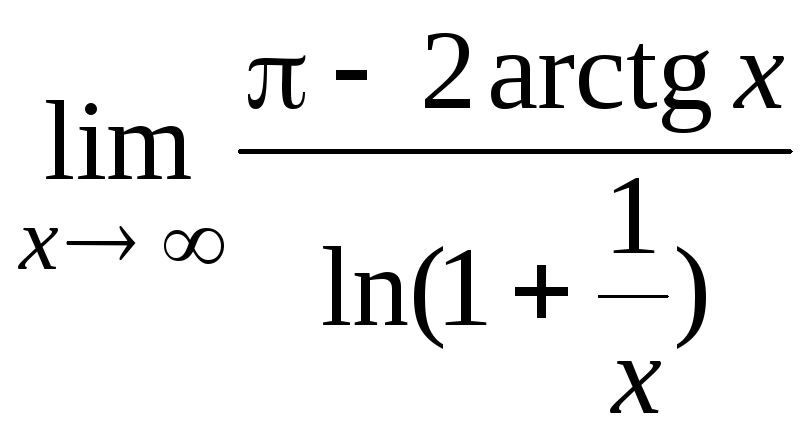 .
.
85.
![]() .
86.
.
86.![]() .
87.
.
87.![]() .
.
88.
![]() .
89.
.
89. .
90.
.
90.![]() .
.
91.![]() .
92.
.
92.![]() .
93.
.
93.![]() .
.
4.8. Формула Тейлора
Пусть
функция
![]()
![]() раз дифференцируема в некоторой
окрестности т.
раз дифференцируема в некоторой
окрестности т.![]() .Тогда
в данной окрестности имеет местоформула
Тейлора
(порядка n)
.Тогда
в данной окрестности имеет местоформула
Тейлора
(порядка n)
![]() ,
,
где
![]() называетсяостаточным
членом формулы Тейлора.
называетсяостаточным
членом формулы Тейлора.
При
![]() имеем:
имеем:
![]() .
.
Эта формула называется
формулой
Маклорена. Остаточный
член формулы Тейлора может быть записан
в различных видах. В частности
![]() ,
где
,
где![]() лежит междуx
и
лежит междуx
и
![]() ,
называется остаточным членом вформе
Лагранжа.
,
называется остаточным членом вформе
Лагранжа.
![]() - “o
– малое” –
остаточный член в
форме Пеано.
Если
- “o
– малое” –
остаточный член в
форме Пеано.
Если
![]() - многочлен степениn,
то формула Тейлора принимает вид:
- многочлен степениn,
то формула Тейлора принимает вид:
![]() ,
т.к.
,
т.к.
![]() .
.
Основные представления по формуле Маклорена с остаточным членом
в форме Пеано
![]() ,
,
 ,
, ,
, ,
,
![]() .
.
Рассмотрим на примерах типы задач, которые решаются с использованием формулы Тейлора.
Пример.
Представить функцию
![]() по формуле Тейлора в окрестности т.
по формуле Тейлора в окрестности т.![]() .
.
Выделим в аргументе
логарифма
![]() .
Имеем
.
Имеем![]() =
=![]() (можно
воспользоваться представлением
(можно
воспользоваться представлением![]() по формуле Маклорена)
по формуле Маклорена)
![]() .
.
Пример.
Вычислить
![]() с точностью до 0.001.
с точностью до 0.001.
Применяя формулу
Маклорена к функции
![]() , получим
, получим
![]() ,
где
,
где
![]() ,
,![]() - остаточный член в форме Лагранжа.
Найдем наименьшее значениеn,
при котором
- остаточный член в форме Лагранжа.
Найдем наименьшее значениеn,
при котором
![]() .
Имеем
.
Имеем![]() .
Наименьшееn,
при котором
.
Наименьшееn,
при котором
![]() равно 3. Следовательно
равно 3. Следовательно![]() .
.
Пример.
Вычислить
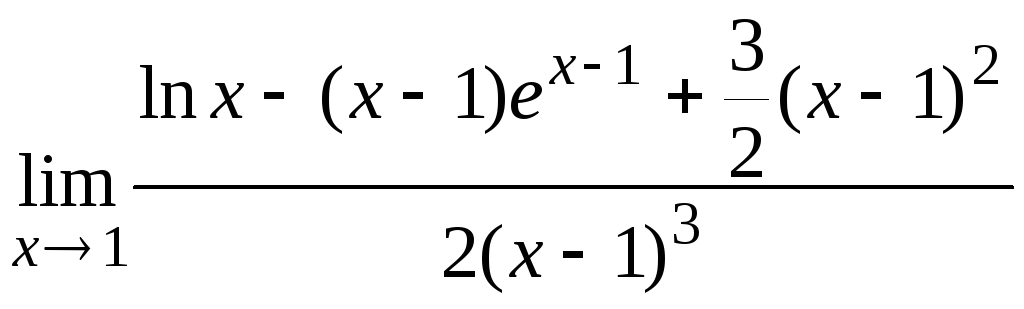 .
.
Применяя
формулу Тейлора, находим:
![]() ;
;

Подставим полученные представления в числитель, получим

 .
.
Задачи для самостоятельного решения
97.Разложить многочлен
![]() по степеням двучлена
по степеням двучлена![]() .
.
98. Функцию
![]() разложить по степенямx,
пользуясь формулой Тейлора.
разложить по степенямx,
пользуясь формулой Тейлора.
99.Написать формулу
Тейлора n-го
порядка для функции
![]() при
при![]() .
.
100. Написать формулу
Тейлора (2n)
порядка для функции
![]() при
при![]() .
.
101. Вычислить поведение
функции
![]() в точке
в точке![]() .
.
Пользуясь формулой Тейлора вычислить пределы.
102.
![]() .
103.
.
103.![]() .
104.
.
104.![]() .
.
105.
![]() .
.
106. Вычислить с
точностью до 0,001 приближенные значения
следующих чисел, используя формулу
Маклорена а) sin
1, б)
![]() ,
в)ln
1,05.
,
в)ln
1,05.
Ответы к задачам главы 4:
1.![]() .
2.
.
2.![]() .
3.
.
3.![]() .
4.
.
4.![]() .
5.
.
5.![]() .
.
6.
![]() .
7.
.
7.![]() .
8.
.
8. .
9.
.
9.![]() .
.
10.
![]() .
11.
.
11.![]() .
12.
.
12.![]() .
.
13.
![]() .
14.
.
14.![]() .
15.
.
15.![]() .
.
16.
![]() .
17.
.
17.![]() .
18.
.
18.![]() .
.
19.
![]() .
20.
.
20.![]() .
21.
.
21.![]() .
.
22.
 .
23.
.
23.![]() .
24.
.
24.![]() .
.
25.
![]() .
26.
.
26.![]() .
.
27.![]() .
28.
.
28.![]() .
.
29.
 .
30.
.
30. .
31.
.
31.![]() .
.
32.
![]() .
33.
.
33.![]() .
.
34.
![]() .
35.
.
35.![]() .
36.
.
36.![]() .
37.
.
37.![]() .
38.
.
38.![]() .
.
39.![]() .
40. –1. 41.
.
40. –1. 41.![]() .
42.
.
42.![]() .
43. 360. 44.
.
43. 360. 44.![]() .
.
45.
![]() .
46.
.
46.![]() .
47.
.
47.![]() .
48.
.
48.![]() .
.
49.
![]() .
50.
.
50.![]() .
51.
.
51.![]() .
52.
.
52.![]() .
53.
.
53.![]() .
.
54.
![]() .
55. (1,1); (-1,-1). 56. Приx
= 0 и при
.
55. (1,1); (-1,-1). 56. Приx
= 0 и при
![]() .
.
57. Касательная
![]() ;
нормаль
;
нормаль![]() .
58.
.
58.![]() .
.
59.
![]() .
60.y
= 2. 61.
.
60.y
= 2. 61.
![]() .
62.
.
62.![]() и
и![]() .
63. Кривые пересекаются в двух точках
под углами
.
63. Кривые пересекаются в двух точках
под углами![]() .
64. 4v
и 2av.
.
64. 4v
и 2av.
65.
![]() .
66.
.
66.![]() .
.
67.
![]() .
68.
.
68.![]()
.69.
![]() .
70.
.
70.![]() .
71.
.
71.![]() .
72.
.
72.![]()
![]() .
73. а) 0,05; б) 0, 805; в) 0,2. 74. 0,355.
75. а)
.
73. а) 0,05; б) 0, 805; в) 0,2. 74. 0,355.
75. а)![]() ,
,
б)
![]() ,
,
в)
![]() .
.
78.
![]()
![]() .
80.
.
80.![]() .82.
0.
.82.
0.
83.
![]() .
84. 2. 85. 2. 86. 1/2. 87. 1/2. 88.cos
3. 89. –2. 90. a.
91. –1.
.
84. 2. 85. 2. 86. 1/2. 87. 1/2. 88.cos
3. 89. –2. 90. a.
91. –1.
92. 0. 93. 1. 94.
![]() .
95. 1/e.
96.
.
95. 1/e.
96.
![]() .
.
97.
![]() .
.
98.
![]() .
.
99.
![]() .
.
100.
![]()
где
![]() .
101. Функция возрастает. (0, 0) – точка
перегиба. 102. 1/4.
.
101. Функция возрастает. (0, 0) – точка
перегиба. 102. 1/4.
103. 1/60. 104. 1/2. 105. 1. 106. а) 0,842; б) 1,648; в) 0,049.
Глава 5. Исследование функций с помощью производных
5.1. Возрастание и убывание функций
Функция f
(x)
называется возрастающей (неубывающей)
на интервале (a,b),
если
![]() таких, что
таких, что![]() выполняется
выполняется![]()
![]() .
.
Функция f
(x)
называется убывающей (невозрастающей)
на интервале (a,b),
если
![]() таких,
что
таких,
что![]() ,
,![]()
![]() .
.
Теорема 1.
Пусть f
(x)
дифференцируема на (a,b).
Тогда если
![]()
![]()
![]() ,
тоf
(x)
возрастающая (убывающая) на (a,b).
,
тоf
(x)
возрастающая (убывающая) на (a,b).
Замечание 1.
Условие
![]()
![]() является необходимым и достаточным для
неубывания (невозрастания)f
(x)
на (a,b).
является необходимым и достаточным для
неубывания (невозрастания)f
(x)
на (a,b).
Интервалы возрастания и убывания функции называются интервалами монотонности.
