Задачи для самостоятельного решения

Выяснить, какие из нижеследующих функций будут периодическими, и определить период.

43. , 44., 45., 46.,

47. , 48., 49..

50. Построить график периодической функции с периодом , которая на промежуткезадана формулой: а), б).

51. Доказать методом полной индукции: если T- период функции , то, где.

1.3. Обратная функция

Пусть двум любым различным элементам множества D соответствуют по закону f два различных элемента множества E. Тогда говорят, что между D и E установлено взаимно однозначное соответствие. Отображение называется обратной функцией по отношению ки обозначаетсяили. Если учесть, что традиционно функцию обозначаютy а аргумент x, то обратной функцией к будет.

Пусть даны непустые множества ии функциии, при этом функцияf двум разным значениям иизX ставит в соответствие разные значения иизY.

Функцию g будем называть обратной к функции f , если для всякого

выполняется

и для всякого выполняется

Функция g, обратная к f, обозначается . Если учесть, что традиционно функцию обозначаютy а аргумент x, то обратной функцией к будет.

Теорема 1.2. Если функция f строго монотонна в области X и имеет область значений Y, то для нее существует однозначная обратная функция , определенная наY и с областью значений X.

Если непрерывная функция не является строго монотонной во всей своей области определения, то, если возможно, область определения разбивают на интервалы, в которых функция строго монотонна, и в каждом таком интервале справедлива теорема 1.2.

Для функций, заданных аналитически , обратную функцию можно получить, выразивx через y, затем, следуя традиции, условимся менять x и y местами.

Пример. Найти обратную функцию для функции .

 Если областью определения функции считать всю числовую ось, то на ней функция не является строго монотонной: нафункция убывает, на- возрастает, и однозначно определенной обратной функции нет. Но на интервалах монотонного изменения функцииобратная функция существует:

а) т.е. обратная функция;

б) , т.е. обратная функция.

Взаимно обратными функциями являются, например,

а);

б),;

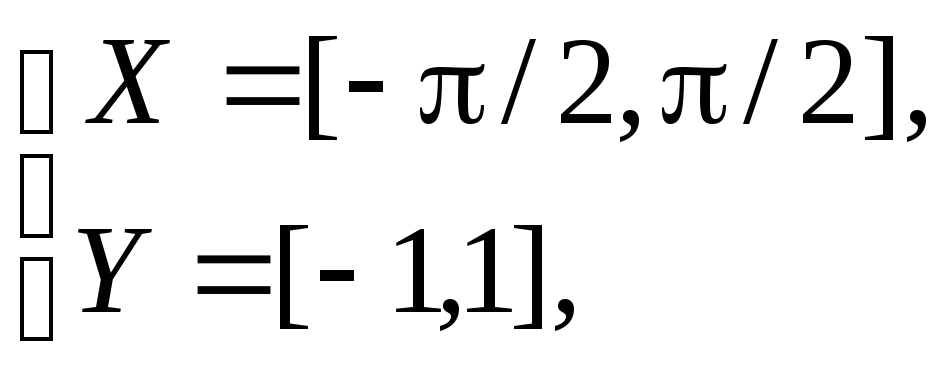
в),;

г),;

д).

Задачи для самостоятельного решения

Найти функцию, обратную данной.

52. , 53., 54., 55.,

56. , 57., 58., 59..

Ответы к задачам главы 1:

1.. 2.. 3.. 4..

5. . 6.. 7.пустое множество. 8.. 9.. 10.. 11.. 12.. 13.. 14.,. 15.а). б). 16.. 17.. 18.. 19.. 20.. 21.. 22.а), б), в), г). д). 23..

24.. 25.. 26..

27..

28. не ограничена. 29.ограничена. 30.ограничена снизу. 31.ограничена снизу.

32.не ограничена. 33.ограничена сверху. 34. Монотонно возрастающая. 35.Монотонно возрастающая. 36.Монотонно возрастающая. 37.Монотонно убывающая. 38.Монотонно возрастает при , монотонно убывает при. 39.а),в),е),ж) – четные, д),з),и) – нечетные, б),г) – ни четные, ни нечетные. 40.. 41..

43.Периодическая, T=. 44.Не периодическая. 45.Не периодическая. 46. Периодическая, . 47. Периодическая,T – любое число. 48.Периодическая, .

49.Не периодическая.

50.

a)

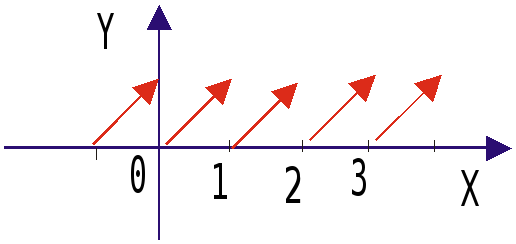
б)

52.. 53.,. 54..

55.. 56.. 57..

58.. 59..