- •Глава 1. Действительные функции одного переменного
- •1.1. Основные понятия и определения
- •Задачи для самостоятельного решения
- •1.2. Некоторые типы функций
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •1.3. Обратная функция
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 1:
- •Глава 2. Предел функции
- •2.1. Предел функции. Основные понятия
- •2.2. Предел дробно-рациональной функции. Иррациональные выражения.
- •Задачи для самостоятельного решения
- •2.3. Бесконечно малые величины. Первый замечательный предел.
- •Задачи для самостоятельного решения
- •2.4. Второй замечательный предел
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 2:
- •Глава 3. Непрерывность функции
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 3:
- •Глава4. Дифференциальное исчисление функции одной переменной
- •4.1. Производная. Дифференцирование явно заданных функций
- •Производная сложной функции. Пусть функция имеет производную в точке, а функцияимеет производную в точке. Тогда сложная функцияимеет производную в точкеи справедливо равенство;.
- •Задачи для самостоятельного решения
- •4.5. Дифференциал
- •Необходимым и достаточным условием дифференцируемости функции в точке является существование у функции производной в данной точке, при этом справедливо равенство .
- •Дифференциалом второго порядка функции называется первый дифференциал первого дифференциала, то естьи он обозначаетсяили.
- •Задачи для самостоятельного решения
- •4.8. Формула Тейлора
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 4:
- •Глава 5. Исследование функций с помощью производных
- •5.1. Возрастание и убывание функций
- •5.2. Точки экстремума функций.
- •Задачи для самостоятельного решения
- •5.3. Исследование функций на выпуклость и вогнутость. Точки перегиба функций.
- •Задачи для самостоятельного решения
- •5.4. Асимптоты графика функции
- •Задачи для самостоятельного решения
- •5.5 Общая схема исследования функций.
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 5:
5.3. Исследование функций на выпуклость и вогнутость. Точки перегиба функций.
Функция
![]() называется
выпуклой (вогнутой) на интервале (a,
b),
если
называется
выпуклой (вогнутой) на интервале (a,
b),
если
![]() касательная расположена выше (ниже)
графика функции.
касательная расположена выше (ниже)
графика функции.
Теорема 1.
Пусть
![]() дважды
дифференцируема на (a,
b),
дважды
дифференцируема на (a,
b),
![]()
![]() тогда
тогда![]() выпуклая (вогнутая) на (a,
b).
выпуклая (вогнутая) на (a,
b).
Точка
![]() называется точкой перегиба графика
функции, если слева от этой точки график
функции выпуклый (вогнутый), а справа –
вогнутый (выпуклый).
называется точкой перегиба графика
функции, если слева от этой точки график
функции выпуклый (вогнутый), а справа –
вогнутый (выпуклый).
Теорема 2
(необходимое
условие перегиба). Пусть
![]() -
точка перегиба графика функции
-
точка перегиба графика функции![]() .
Тогда или
.
Тогда или![]() или
или![]() не существует.
не существует.
Теорема 3 (достаточное
условие перегиба). Пусть
![]() дважды
дифференцируема в некоторой окрестности
т.
дважды
дифференцируема в некоторой окрестности
т.![]() и либо
и либо![]() существует и конечна, либо
существует и конечна, либо![]() не существует и
не существует и![]() меняет знак при переходе через т.
меняет знак при переходе через т.![]() .
Тогда
.
Тогда![]() -
точка перегиба графика функции.
-
точка перегиба графика функции.
Пример.
Найти интервалы выпуклости, вогнутости
и точки перегиба графика функции
![]() .
.
Область определения D(y)=R. Вычислим вторую производную.
![]() .
.
![]() .
.
Точки возможного
перегиба :![]() ,
т.к.
,
т.к.![]() и
и![]() не существует и
не существует и![]() .
Проверим смену знака
.
Проверим смену знака![]() :
:

 -
- +
знак
-
- +
знак
![]() .
.
-6 0
Следовательно, точка
перегиба графика одна – (0,0). Функция
выпукла на интервале
![]() и вогнута на
и вогнута на![]() .
.
Задачи для самостоятельного решения
22. Показать, что
график функции
![]() везде выпуклый.
везде выпуклый.
23. Доказать, что если график функции везде выпуклый или везде вогнутый, то эта функция не может иметь более одного экстремума.
Найти точки перегиба и интервалы вогнутости и выпуклости для следующих функций.
24.
![]() .
25.
.
25.![]() 26.
26.![]() .
.
27.
![]() .
28.
.
28.![]() .
29.
.
29.![]() .
.
30.
![]() .
.
5.4. Асимптоты графика функции
Пусть существует
такая прямая, что расстояние до нее от
точки
![]() графика функции
графика функции![]() стремится к нулю при
стремится к нулю при![]() стремящемся к бесконечности. Тогда
прямая называетсяасимптотой
графика функций.
Прямая
стремящемся к бесконечности. Тогда
прямая называетсяасимптотой
графика функций.
Прямая
![]() называетсявертикальной
асимптотой,
если хотя бы один из пределов:
называетсявертикальной
асимптотой,
если хотя бы один из пределов:
![]() или
или![]() равен бесконечности.
равен бесконечности.
Если существуют
конечные пределы
![]() и
и![]() ,
то прямая
,
то прямая![]() естьнаклонная
асимптота
графика функции
естьнаклонная
асимптота
графика функции
![]() .
Пределы могут не существовать или быть
бесконечными при
.
Пределы могут не существовать или быть
бесконечными при![]() и существовать при
и существовать при![]() (левая наклонная асимптота).
(левая наклонная асимптота).
Если функция
![]() может быть представлена в виде
может быть представлена в виде![]() ,
где
,
где![]() -
бесконечно малая при
-
бесконечно малая при![]() ,
то
,
то![]() есть наклонная асимптота.
есть наклонная асимптота.
Пример.
Найти асимптоты графика функции
![]() .
.
Найдем область
определения функции:
![]()
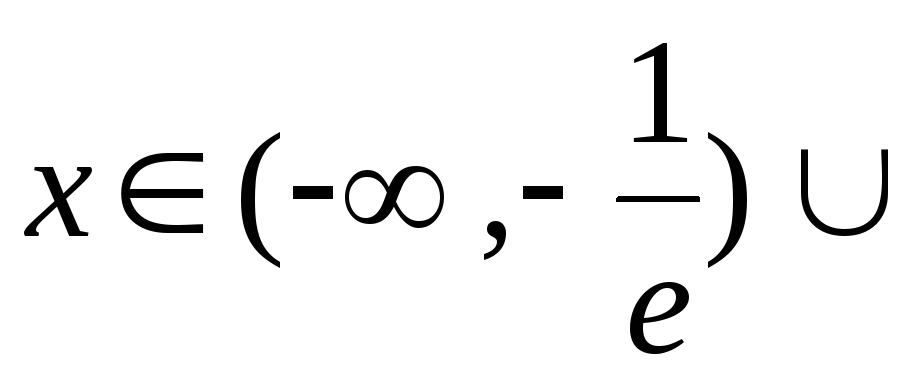
![]() ,
,
![]() ,
,
![]() (
применить правило Лопиталя)=
(
применить правило Лопиталя)=![]() .
Следовательно
.
Следовательно![]() - вертикальная асимптота, а
- вертикальная асимптота, а![]() не является асимптотой. Проверим наличие
наклонной асимптоты.
не является асимптотой. Проверим наличие
наклонной асимптоты.![]() ,
,![]() (
(![]() ,
применим правило Лопиталя)=
,
применим правило Лопиталя)=![]() .
Следовательно
.
Следовательно![]() - наклонная асимптота.
- наклонная асимптота.
Задачи для самостоятельного решения
Найти асимптоты графиков следующих функций:
31.
![]() .
32.
.
32.![]() .
33.
.
33.![]() .
34.
.
34.![]() .
.
35.
![]() .
36.
.
36.![]() .
37.
.
37.![]() .
38.
.
38.![]() .
.
5.5 Общая схема исследования функций.
Для построения
графика функции
![]() нужно провести исследование по следующей
схеме:
нужно провести исследование по следующей
схеме:
Область определения функции
 .
.Четность, нечетность, периодичность. Точки пересечения графика
 с осями координат.
с осями координат.Нахождение точек из области определения, в которых либо
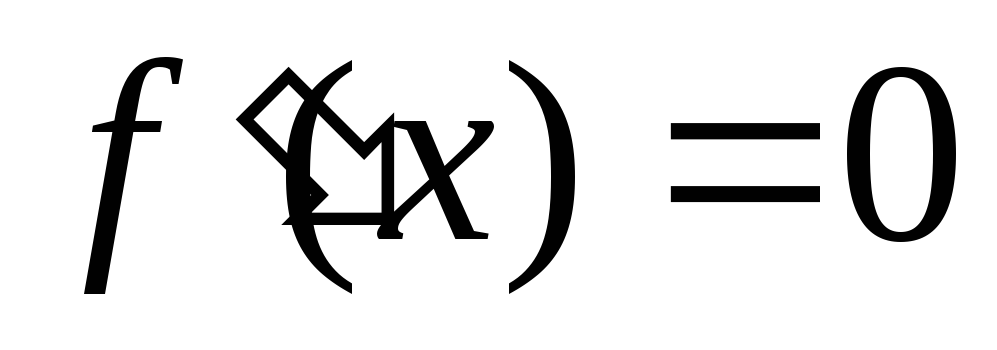 , либо
, либо не существует.
не существует.Нахождение точек из области определения, в которых либо
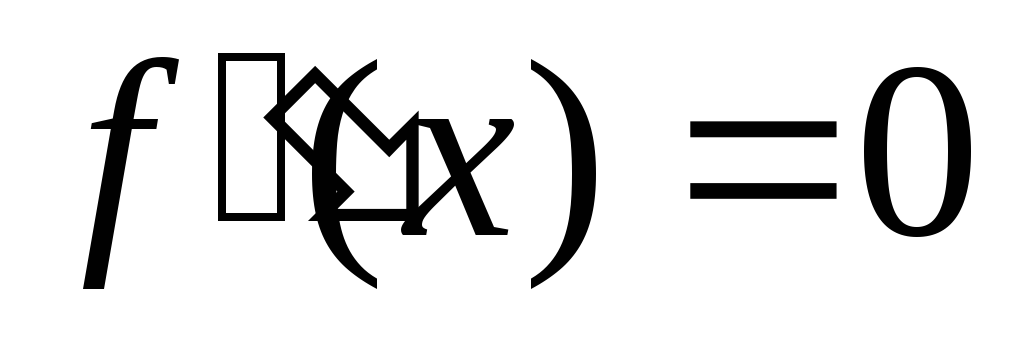 ,
либо
,
либо не существует.
не существует.Нахождение экстремумов, перегибов, интервалов возрастания и убывания, выпуклости и вогнутости графика по сводной таблице.
Асимптоты.
Построение графика.
Пример.
Провести полное исследование функции
![]() и построить график.
и построить график.
В соответствие со схемой имеем:
 .
.Функция общего вида. График проходит через точку (0,0).
 .
Точки возможного экстремума имеют
абсциссы
.
Точки возможного экстремума имеют
абсциссы
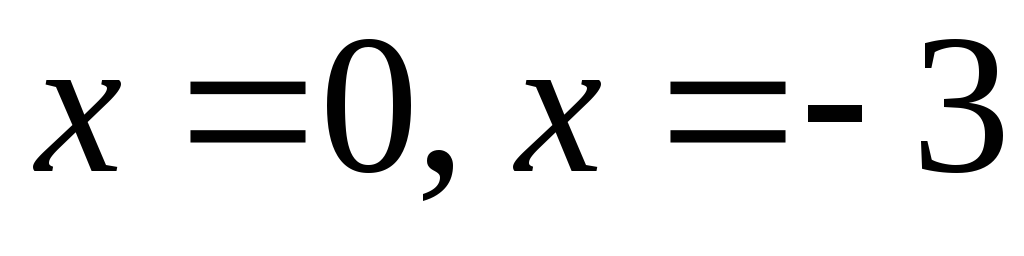 .
. .
Точка возможного перегиба имеет абсциссу
x
=0.
.
Точка возможного перегиба имеет абсциссу
x
=0.Результаты сводим в таблицу
|
x |
|
–3 |
(–3, –1) |
(–1, 0) |
0 |
|
|
|
+ |
0 |
– |
+ |
0 |
+ |
|
|
– |
|
– |
- |
0 |
+ |
|
y |
|
|
|
|
0 |
|
|
|
|
лок. max |
|
|
перегиб |
|

 .
Следовательно
.
Следовательно
 -
вертикальная асимптота. Выделим целую
часть
-
вертикальная асимптота. Выделим целую
часть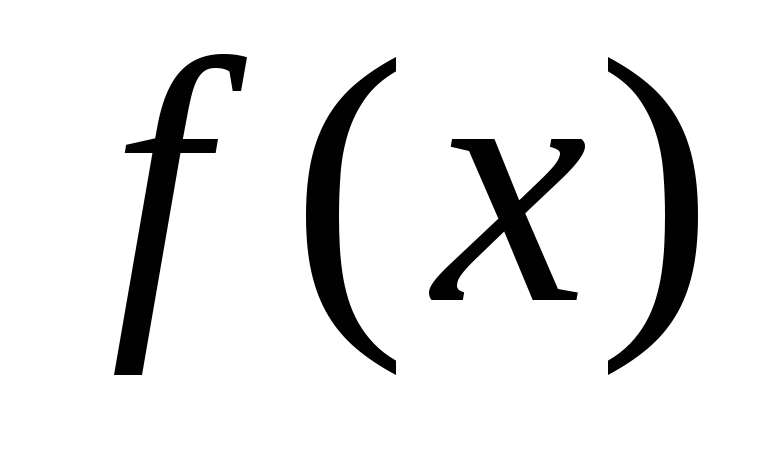 .
. и так как
и так как -
бесконечно малая при
-
бесконечно малая при ,
то
,
то -
наклонная асимптота.
-
наклонная асимптота.Рисунок .