1.1.9. Практичне заняття

Приклад 1.Знайти похідну функції.

Розв’язок. Запишемо функцію у виглядіі використаємо правило знаходження похідої степеневої функції

.

Приклад 2. Знайти похідну функції.

Розв’язок.Вважаючи, щоy = u⁵, деu = x² – 2x + 3, аu' = ,відповідно до правила диференціювання складної функції (1.7) матимемо

y' = 5u⁴u' = 10 (x – 1)(x² – 2x + 3)⁴.

Приклад 3.Знайти похідну функціїy = sin³4x.

Розв’язок.Позначившиy = u³,u = sinv,v = 4xi, враховуючи, щоy' = 3u²u', аu'= (sinv)'  v', деv' = 4, знайдемоy' = 12sin²4xcos 4x.

Примітка. Маючи достатні навички, проміжкові змін­ні u та v не записують, вводячи їх лише в уяві (подумки).

Приклад 4. Розчинення лікарської речовини з таблетки опису­єть­ся рівнянням, де– початкова маса таблетки;m– нерозчинена маса в момент часуt;k– стала, що характеризує процес розчинення (константа елімінації). Записати рівняння для швидкості розчинення.

Розв’язок.Оскільки похідна дорівнює швидкості зміни функції, то швидкість розчинення:.

Отже, швидкість розчинення пропорційна масі таблет­ки, яка залишилася.

Приклад 5. Знайти похідну першого, другого та третього порядку від функціїf(x) = e^xsin x.

Розв’язок.

f ' (x) = e^xsinx + e^xcosx = e^x (sinx + cosx);

f '' (x) = [e^x(sinx + cosx)]' = e^x (sinx + cosx) +

(cosx – sinx)e^x = 2e^x cos x;

f ''' (x) = (2e^xcosx)' = 2(e^xcosx – e^xsinx) = 2e^x(cosx – sinx).

Приклад 6.Знайти диференціал функціїy = ln x².

Розв’язок.Знайдемо похідну функції. Ско­рис­тав­шись формулою, отримаємо.

Приклад 7.Чисельність популяції бактерій з часомtзмінюється за законом

,

де N₀ – початкова кількість бактерій у популяції,С– деяка константа. Знайти максимальний розмір популяції, якщоN₀ = 10³;С = 400.

Розв’язок.Обчислимо похідну

.

З умови С – t² = 0 (N' = 0) знайдемо критичні точки. Змісту задачі відповідає лише, у ній функція має максимум, оскільки при(наприклад, приt = 0) – функція зростаюча, а при,функція спадає. Мак­симальна чисельність популя­ції .

Приклад 8.Вміст глюкози в крові хворого при вливанні крап­лями визначається рівнянням:, деа іb– констан­ти,t– час. Побудувати графік, знайти рівноважний вміст глюкози.

Р

Мал. 1.7.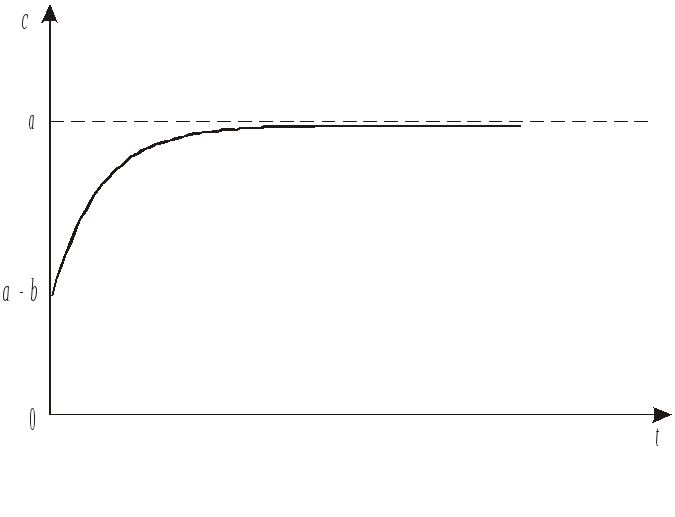

озв’язок.Функціявизначена і неперервна на всій числовій прямій, однак, фізичний зміст вона має лише при. Проведемо дослід­жен­ня у цій області. Як­що, то. Пря­­має гори­зон­таль­­­­­ною асимптотою, ос­кіль­­­­ки при. Похіднане може бути рівною нулю і при всіх можливих зна­чен­няхє додатньою, тобто досліджувана функція монотонно зростаюча у всій об­лас­ті визначення. Для всіхt(0; ) функція додатня.

Друга похід­на є від’ємною для всіх зна­ченьі прямує до ну­ля лише, якщо . Отже, досліджувана функ­­ція направлена випукліс­тю вгору і не має точок перегину. Графік її подано на мал.1.7. Рівноважний вміст глюкози дорів­нюєі досягається при .

Приклад 9.Дослідити на екстремум функцію, яка описує зміну концентрації лікарського препарату у крові пацієнта при перораль­ному та внутрішньом’язовому вве­ден­ні,

,

д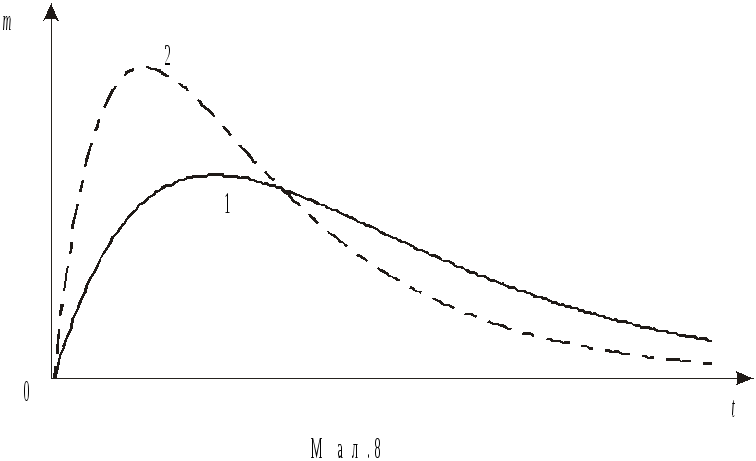еM₀– початкова маса препарату у депо,k– константа елімінації,r – деяка константа, яка характеризує швидкість всмоктування.

Розв’язок.Похідна перетво­рюєть­ся в нуль, якщо. Прологарифмувавши цей вираз, бачимо, що критичною точкою є. Перевіряючи зміну знака похідної, враховуємо, щоk > r.Переконуємось, що в даній точці функція має екстремум. На мал.1.8 графічно подано залежністьm(t) для двох різних значеньr(r₂>r₁) при однакових значенняхk: крива 1 описує процес, який реалізується при поступовому над­ходженні препарату в депо; крива 2 – випадок швидкого надходження, така ситуація має місце, наприклад, при прийомі ліків з додаванням бікарбонату натрію (шипучих таблеток). Порівняння графіків свідчить, що повільне всмоктування може забезпечити майже постійну кон­цен­т­рацію препарату в крові на тривалий проміжок часу.