
- •78 Елементи диференціального числення Розділ 1. Математична обробка медико-біологічної інформації
- •Елементи диференціального числення
- •1.1.1.Похідна та диференціал функції
- •Геометричне тлумачення похідної і диференціала
- •Фізичне тлумачення похідної і диференціала
- •1.1.2. Основні правила диференціювання
- •1.1.3. Таблиця похідних основних елементарних функцій
- •1.1.4. Правило диференціювання складної функції
- •1.1.5. Похідні вищого порядку
- •1.1.6. Дослідження функцій на монотонність.Максимуми та мінімуми функцій
- •1.1.7. Випуклість та увігнутість графіка функції.Точки перегину
- •1.1.8. Побудова графіків функцій
- •1.1.9. Практичне заняття
- •1.1.10. Завдання для самостійної роботи
- •Функції декількох змінних
- •1.2.1. Частинні похідні і диференціали функції декількох змінних
- •1.2.2. Повний диференціал
- •1.2.3. Застосування диференціала функції для обчислення похибок
- •Правила визначення похибок
- •1.2.4. Практичне заняття
- •1.2.5. Завдання для самостійної роботи
- •Елементи інтегрального числення
- •1.3.1. Первісна.Невизначений інтеграл
- •1.3.2. Властивості невизначеного інтегралу
- •1.3.3. Таблиця найпростіших інтегралів
- •1.3.4. Основні методи інтегрування
- •1.3.5.Визначений інтеграл
- •1.3.6. Властивості визначеного інтеграла
- •1.3.7. Формула Ньютона–Лейбніца
- •1.3.8. Практичне заняття
- •1.3.9. Завдання для самостійної роботи
- •Елементи теорії Звичайних диференціальних рівнянь
- •1.4.1. Поняття про диференціальні рівняння
- •1.4.2. Лінійні диференціальні рівняння
- •Лінійні диференціальні рівняння першого порядку
- •1.4.3. Диференціальні рівняння зі змінними,що розділяються
- •1.4.4. Лінійні диференціальні рівняння другого порядку з постійними коефіцієнтами
- •1.4.5.Практичне заняття
- •1.4.6. Завдання для самостійної роботи
- •Основи теорії йМовірностей та математичної статистики
- •1.5.1. Класифікація явищ.Частота та ймовірність події
- •1.5.2. Теорема додавання ймовірностей
- •1.5.3. Теорема множення ймовірностей
- •1.5.4. Формула повної ймовірності.Формули Байєса
- •1.5.5. Повторні випробування. Формула Бернуллі
- •1.5.6. Випадкова величина,дискретні та неперервні випадкові величини
- •1.5.7. Інтегральна та диференціальна функції розподілу
- •1.5.8. Основні кількісні характеристики розподілу випадкових величин
- •1.5.9. Основні закони розподілу випадкових величин
- •1.5.10. Кореляційна залежність
- •1.5.11. Практичне заняття
- •1.5.12. Завдання для самостійної роботи
1.3.6. Властивості визначеного інтеграла
1. Постійний множник можна виносити за знак інтеграла:
![]() .
.
2. Інтеграл від алгебраїчної суми функцій дорівнює сумі визначених інтегралів від доданків:
![]() .
.
3. Якщо відрізок [a, b] = [a, c] + [c, b], то
![]() .
.
4. Теорема про середнє. Якщо функціяf (x)неперервна на[а, b], то у межах[а, b]існує точкастака, що
![]() .
.
Геометричний зміст цієї теореми: площу криволінійної трапеції можна виразити через площу прямокутника з тією ж основою, що й трапеція, і стороною, яка дорівнює значенню підінтегральної функції при деякому проміжному значенні аргументу.
5. При перестановці меж інтегрування інтеграл змінює знак на протилежний
![]() .
.
Цю властивість легко зрозуміти, якщо скористатись теоремою про середнє та взяти до уваги, що(b – а) = – (а – – b).
6. Якщо межі інтегрування нескінченно мало відрізняються одна від одної, то
![]() .
.
7. Похідна по xвід інтеграла зі змінною верхньою межеюxдорівнює підінтегральній функції при значенні змінної, рівна значенню верхньої межі(t = x):
![]() ,
,
якщо підінтегральна функція не залежить від x.
Таким чином, інтеграл зі змінною верхньою межею є однією із первісних для підінтегральної функції.
1.3.7. Формула Ньютона–Лейбніца
Знаючи, що
![]() ,
знайдемоС.
Прийнявших
=
а,
матимемо
,
знайдемоС.
Прийнявших
=
а,
матимемо![]() .
ЗвідсиF(a)
+ C = 0,
тобтоC
= =
–
F(а)
. Отже,
.
ЗвідсиF(a)
+ C = 0,
тобтоC
= =
–
F(а)
. Отже,
![]() .
.
Перейдемо до означеного інтеграла, прийнявши х = b. Остаточно будемо мати
![]() . (1.15)
. (1.15)
Ця формула називається формулою Ньютона–Лейбніца.
Таким чином, задача обчислення визначеного інтеграла зводиться до знаходження первісної (тобто невизначеного інтеграла); потім потрібно обчислити значення первісної прих = bіх = ата знайти різницю цих значень.
Приклад. У деяких діагностичних методиках користуються препаратами з ізотопними індикаторами. Швидкість зміни концентраціїСтакого препарату в організмі з плином часу описується законом:
![]() ,
,
де K– константа в умовах експерименту. Знайти концентрацію препарату в момент часуt = 0.5год.
Розв’язок.Шукана концентрація визначається інтегралом
![]() .
.
Знайдемо первісну і скористаємось формулою Ньютона – Лейбніца (1.15). Звідси матимемо
C= – K(e–0.5
–e0) =K(1
– ![]() ).
).
1.3.8. Практичне заняття
Приклад 1. Обчислити невизначений інтеграл
![]() .
.
Розв’язок.Використовуючи властивості 1 і 2 невизначеного інтеграла, даний інтеграл можна записати у вигляді:
![]() .
.
Використавши формулу 1 з таблиці невизначених інтегралів, отримаємо
![]() .
.
Приклад 2.Обчислити інтеграл![]() .
.
Розв’язок.Припустивши, щоt
= sinx,
знайдемо dt
=
![]() ,і підінтегральний вираз можна перетворити
до вигляду:sin2xcos
xdx = t2dt.
,і підінтегральний вираз можна перетворити
до вигляду:sin2xcos
xdx = t2dt.
Отже,
![]() .
.
Приклад 3.Обчислити інтеграл![]() .
.
Розв’язок.Обчислимо цей інтеграл
методом інтегрування
по частинах (1.14). Запишемо
підінтегральну функцію у вигляді
добутку двох співмножників – функціїu
=
lnx
idυ
=
x3dx.
Тоді![]() .
Використавши формулу (1.14),
отримаємо:
.
Використавши формулу (1.14),
отримаємо:

1.3.9. Завдання для самостійної роботи
Користуючись табличними інтегралами і перетворюючи належним чином підінтегральні вирази, знайдіть:
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
Знайти інтеграли методом заміни змінної:
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22.
|
|
23.
|
24.
|
|
25.
|
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
Знайти інтеграли методом інтегрування по частинах:
|
31.
|
32.
|
|
33.
|
34.
|
|
35.
|
36.
|
|
37.
|
38.
|
|
39.
|
40.
|
Використовуючи формулу Ньютона–Лейбніца, обчислити визначені інтеграли:
|
41.
|
42.
|
|
43.
|
44.
|
|
45.
|
46.
|
|
47.
|
48.
|
|
49.
|
50.
|
|
51.
|
52.
|
|
53.
|
54.
|
Обчислити площі фігур, обмежених лініями:
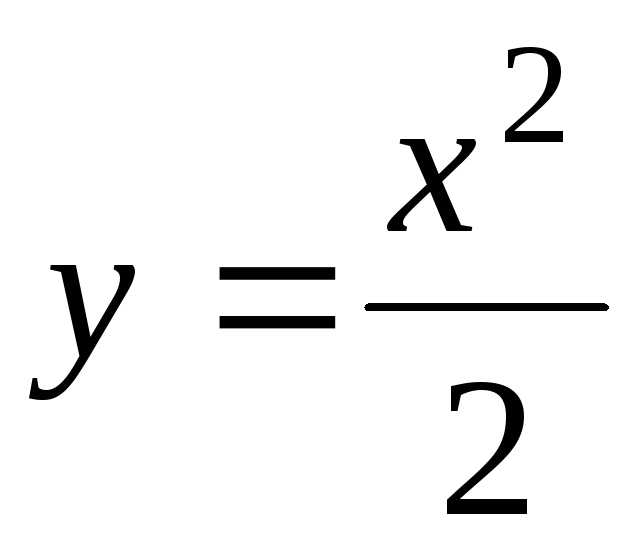 ;
x = 1;
x = 3
і віссю абсцис.
;
x = 1;
x = 3
і віссю абсцис.
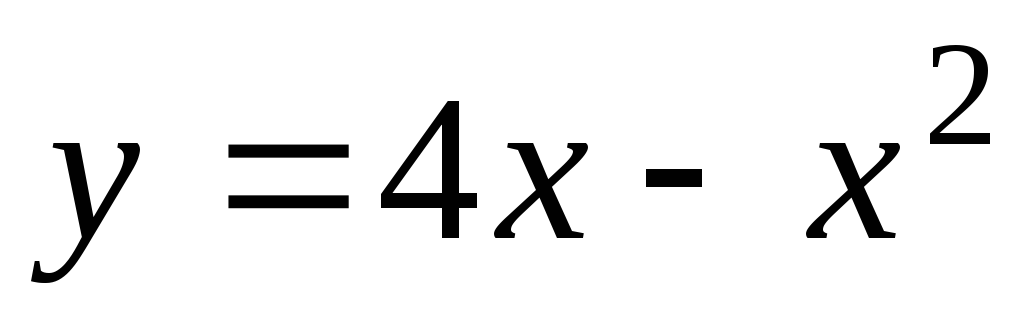 і віссю абсцис.
і віссю абсцис.y = sin x; x = 0;
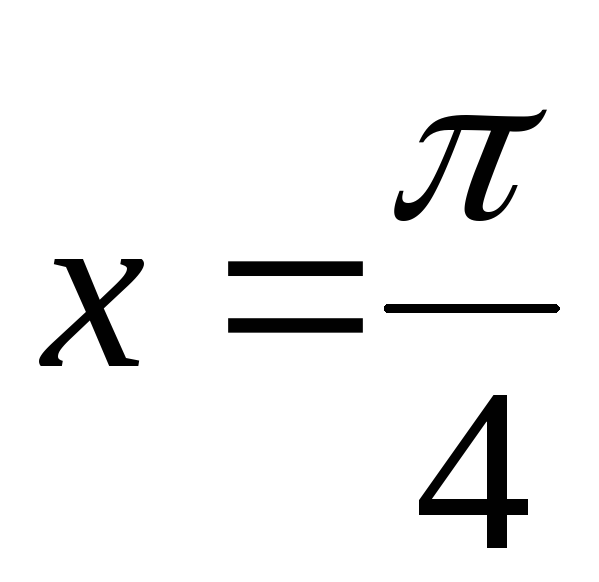 .
.y = tg x;
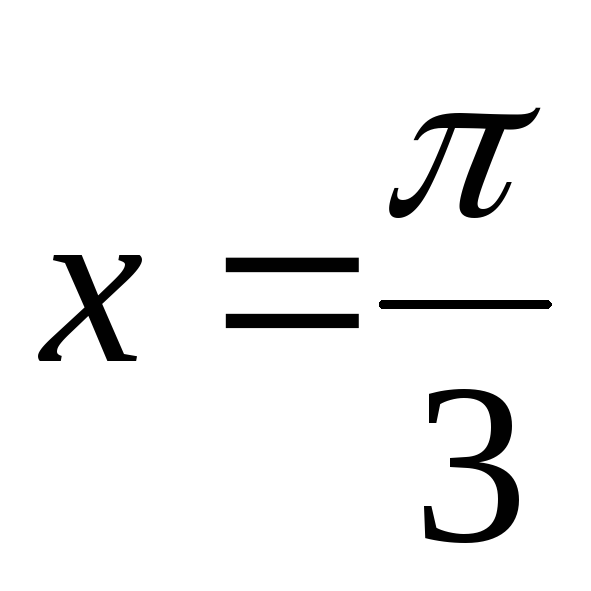 і віссю абсцис.
і віссю абсцис.y = x2; y = 2 – x2.
y = lnx; y = 0; x = 0.
y = e – x; y = 0; x = 1; x = 2.
y = 2x; y = 2; x = 0.
y = 2x – x2; y = x.
y = x3; x = 2; x = 3.
Знайти приріст чисельності популяції за проміжок часу від t1 до t2, якщо швидкість приросту визначається формулою V(t) = Сеkt, де С і k – величини сталі в умовах задачі.
Знайти об’єм рідини Q, яка протікає по трубі радіусом R за 1 с. Залежність швидкості рідини від відстані до осі труби r задається формулою:
![]() .
.
Примітка.![]() –
величина стала в умовах задачі.
–
величина стала в умовах задачі.
