Вариант 38

1. Прямая как пересечение двух плоскостей.

2. Упрощение уравнения центральной кривой 2-го порядка с помощью ортогональных преобразований координат.

3. В ортонормированной системе координат пространства даны точки ,,, 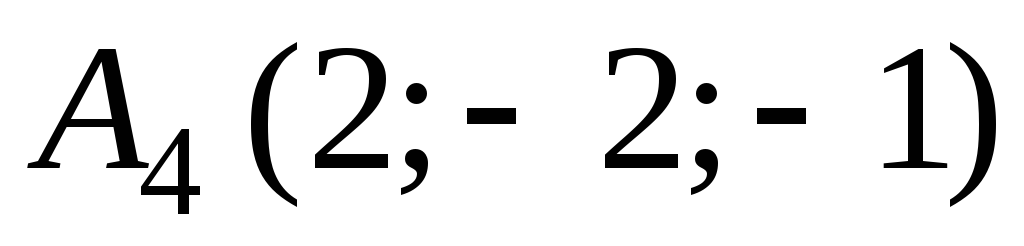. Найти угол между прямойи плоскостью.

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

5. В ортонормированной системе координат плоскости составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что прямая− ее асимптота, а расстояние между ее директрисами равно 64/5.

Вариант 39

1. Преобразование базисов.

2. Определение поверхностей второго порядка. Приведенное уравнение поверхности второго порядка.

3. В ортонормированной системе координат пространства даны точки ,,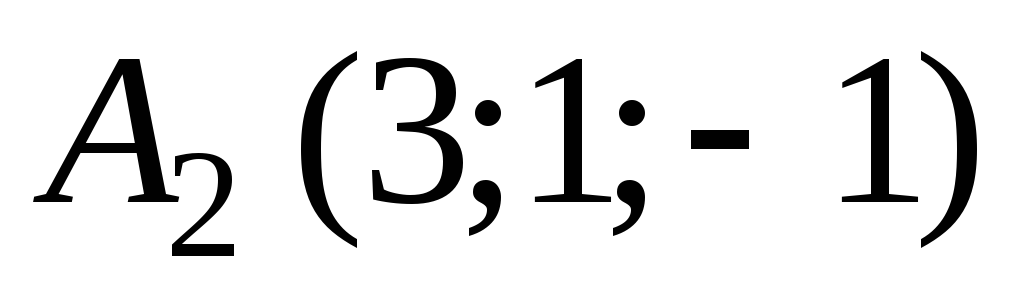,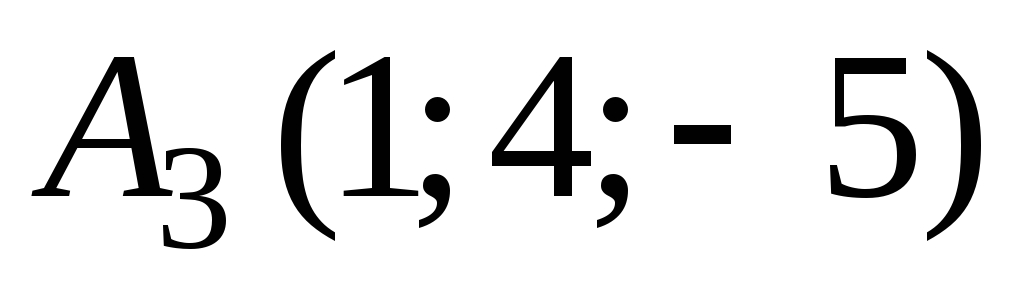. Найти угол между прямойи плоскостью .

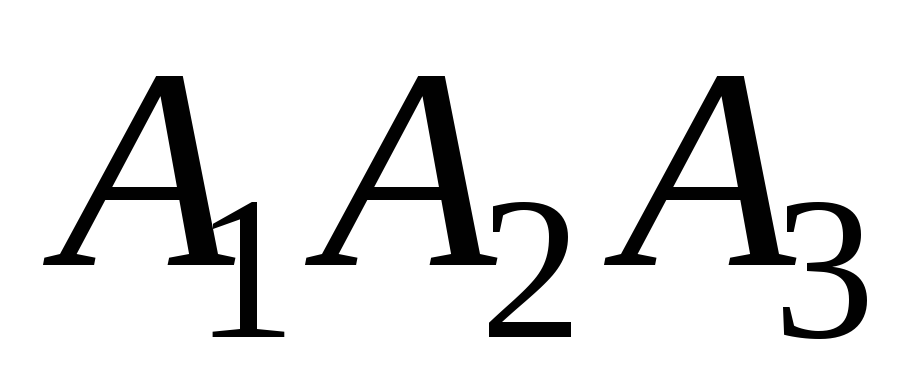4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

5. В ортонормированной системе координат плоскости составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что прямая− ее асимптота, а расстояние между ее директрисами равно 64/5.