
Вариант 13
Расстояние от точки до плоскости.
Касательные к гиперболе.
В ортонормированной системе координат пространства даны точки
 ,
, ,
, ,
, .
Найти угол между прямой
.
Найти угол между прямой и плоскостью
и плоскостью .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В ортонормированной системе координат
 плоскости составить уравнение гиперболы,
если ее эксцентриситет
плоскости составить уравнение гиперболы,
если ее эксцентриситет ,
а фокусы совпадают с фокусами эллипса
,
а фокусы совпадают с фокусами эллипса .
.
Вариант 14
Преобразование базисов.
Касательные к параболе.
В ортонормированной системе координат пространства даны точки
 ,
, ,
, ,
, .
Найти угол между прямой
.
Найти угол между прямой и плоскостью
и плоскостью
 .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В ортонормированной системе координат
 плоскости составить уравнение гиперболы,
фокусы которой расположены на оси
абсцисс симметрично относительно
начала координат, зная, что прямая
плоскости составить уравнение гиперболы,
фокусы которой расположены на оси
абсцисс симметрично относительно
начала координат, зная, что прямая − ее асимптота, а расстояние между ее
директрисами равно 64/5.
− ее асимптота, а расстояние между ее
директрисами равно 64/5.
Вариант 15
Взаимное расположение двух плоскостей.
Касательные к параболе.
В аффинной системе координат пространства составить уравнение плоскости, проходящей через точки
 ,
,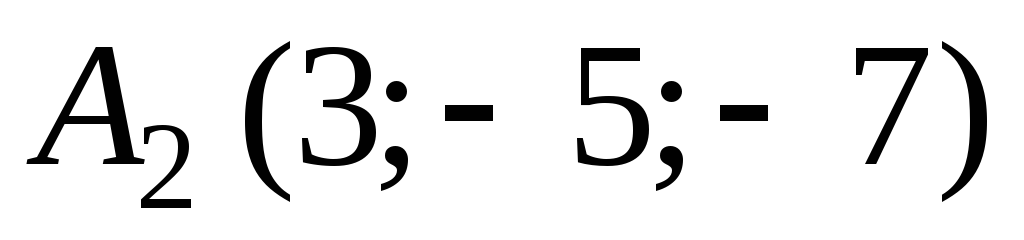 ,
, .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В аффинной системе координат
 плоскости составить уравнения касательных
к параболе
плоскости составить уравнения касательных
к параболе ,
проведенных из точки
,
проведенных из точки .
.
Вариант 16
Взаимное расположение прямой и плоскости.
Преобразование уравнения кривой второго порядка при переходе к новой аффинной системе координат.
В ортонормированной системе координат пространства даны точки
 ,
, ,
, ,
,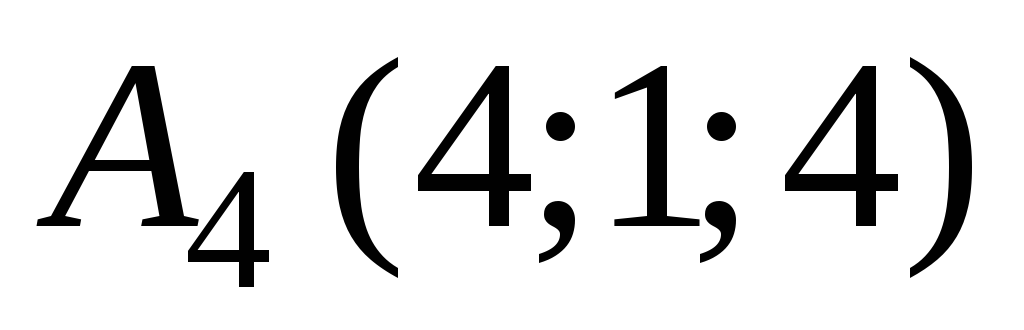 .
Найти уравнения прямой, проходящей
через точку
.
Найти уравнения прямой, проходящей
через точку перпендикулярно плоскости
перпендикулярно плоскости .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В ортонормированной системе координат
 плоскости составить уравнение гиперболы,
если
плоскости составить уравнение гиперболы,
если и
и − ее фокусы, а прямая
− ее фокусы, а прямая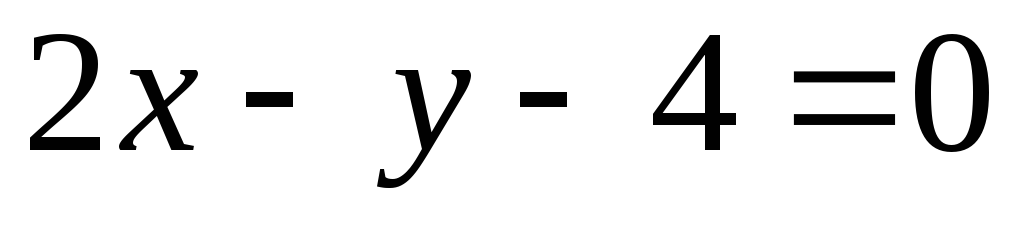 касается этой гиперболы.
касается этой гиперболы.
Вариант 17
Пучок плоскостей.
Директориальное свойство гиперболы.
В аффинной системе координат пространства составить канонические и параметрические уравнения прямой, проходящей через точки
 и
и .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
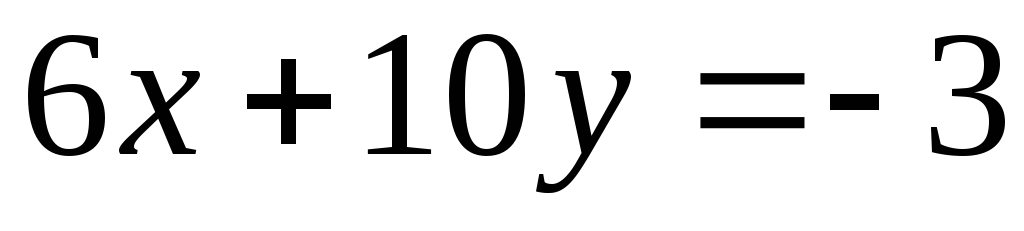 ,
,
 ,
,
 .
.В аффинной системе координат
 плоскости составить уравнения касательных
к эллипсу
плоскости составить уравнения касательных
к эллипсу ,
параллельных прямой
,
параллельных прямой .
.
ВАРИАНТ 18
Канонические и параметрические уравнения прямых.
Оптическое свойство параболы.
В аффинной системе координат пространства составить уравнение плоскости, проходящей через точки
 ,
,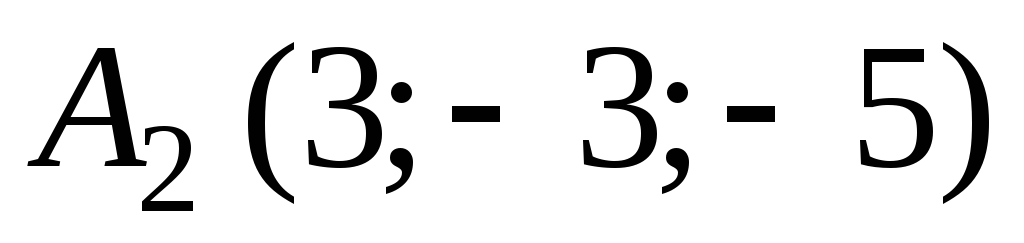 ,
, ,
, .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В ортонормированной системе координат
 плоскости определить точки гиперболы
плоскости определить точки гиперболы ,
расстояния от которых до ее правого
фокуса равно 4,5.
,
расстояния от которых до ее правого
фокуса равно 4,5.
ВАРИАНТ 19
Прямая как пересечение двух плоскостей.
Полярное уравнение гиперболы.
В ортонормированной системе координат пространства даны точки
 ,
, .
Составить уравнение плоскости, проходящей
через точку
.
Составить уравнение плоскости, проходящей
через точку перпендикулярно прямой
перпендикулярно прямой .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В аффинной системе координат
 плоскости найти уравнения касательных,
проведенных к эллипсу
плоскости найти уравнения касательных,
проведенных к эллипсу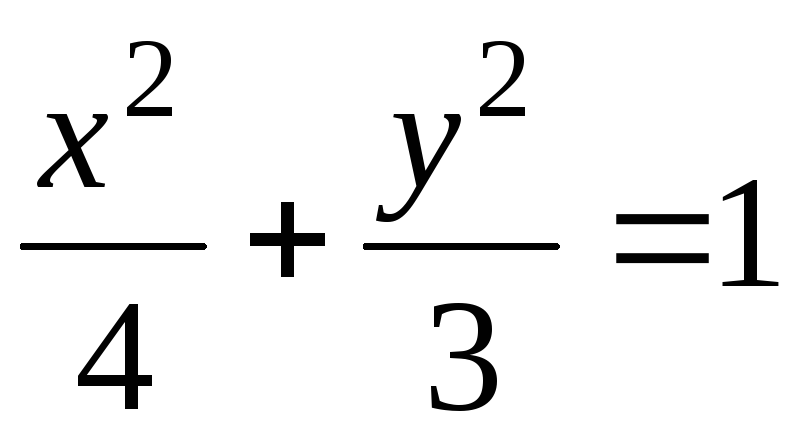 из точки
из точки .
.
ВАРИАНТ 20
Расстояние между двумя прямыми в пространстве.
Полярное уравнение параболы.
В ортонормированной системе координат пространства даны точки
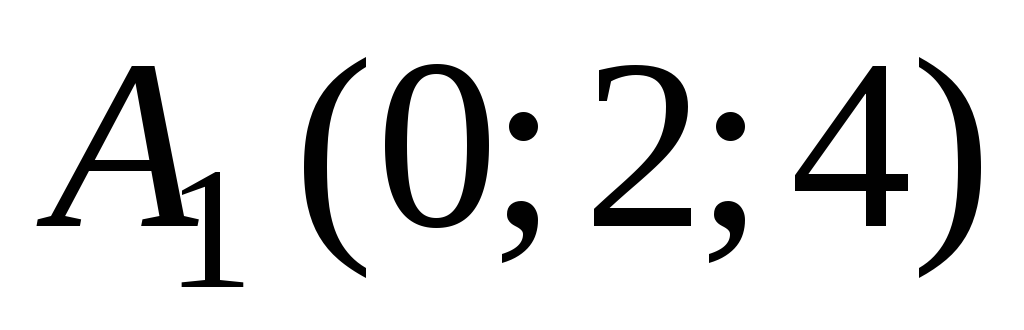 ,
, ,
,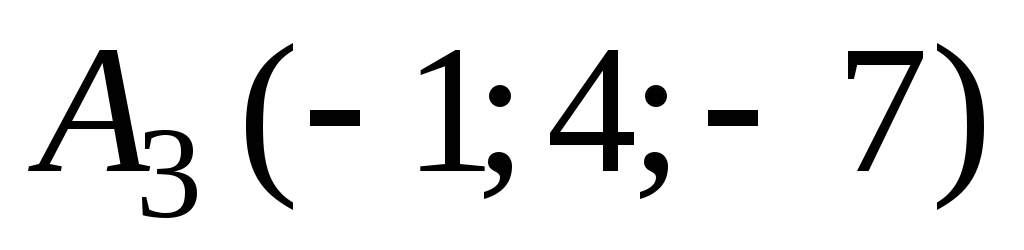 ,
, .
Составить уравнение плоскости, которая
содержит прямую
.
Составить уравнение плоскости, которая
содержит прямую и перпендикулярна плоскости
и перпендикулярна плоскости .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В аффинной системе координат
 плоскости составить уравнение прямой,
которая касается параболы
плоскости составить уравнение прямой,
которая касается параболы и параллельна прямой
и параллельна прямой .
.
ВАРИАНТ 21
Взаимное расположение прямой и плоскости.
Ортогональная классификация кривых 2-го порядка.
В аффинной системе координат пространства составить канонические и параметрические уравнения прямой, проходящей через точки
 и
и .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
 .
.В ортонормированной системе координат
 плоскости найти точки эллипса
плоскости найти точки эллипса ,
расстояние от которых до левого фокуса
эллипса равно 2,5.
,
расстояние от которых до левого фокуса
эллипса равно 2,5.
ВАРИАНТ 22
Ортогональные преобразования координат на плоскости.
Асимптотические направления для кривых 2-го порядка. Асимптоты гиперболы.
В ортонормированной системе координат пространства составить уравнение прямой, проходящей через точку
 перпендикулярно плоскости, содержащей
точки
перпендикулярно плоскости, содержащей
точки ,
, ,
, .
.Найти точки пересечения трех плоскостей, заданных в аффинной системе координат
 уравнениями
уравнениями
 ,
,
 ,
,
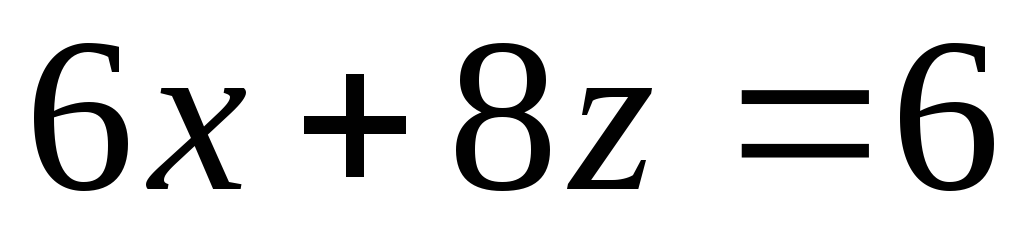 .
.В ортонормированной системе координат
 плоскости на параболе
плоскости на параболе найти точки, фокальный радиус которых
равен 13.
найти точки, фокальный радиус которых
равен 13.
