Выпуклость

Среди всех гладких кривых на плоскости выделяется класс кривых, не имеющих точек перегиба. Такие кривые мы будем называть выпуклыми. Маленькая окрестность любой точки на выпуклой кривой лежит по одну сторону от своей касательной и может пересекаться с любой прямой не более чем в двух точках (рис. 7).

Рис. 7.

Понятое выпуклости легко и естественно обобщается для сферы. «Прямыми» на сфере будем называть большие окружности (экваторы). Кривая на сфере называется выпуклой в данной точке, если окрестность кривой в этой точке лежит по одну сторону от касательного экватора.

Рис. 8.

Выпуклые кривые встречаются в природе, когда заряженная частица мчится поперек линий магнитного поля. Согласно правилу буравчика» она будет закручиваться все время в одну^: и ту же сторону (рис. 9).

Рис. 9.

Будем говорить, что выпуклые кривые — одного типа, если их можно продеформировать друг в друга так, чтобы они оставались не только гладкими, но и выпуклыми в каждой точке. Это условие сильнее, чем то, что было раньше. Две однотипные в старом смысле кривые могут оказаться совершенно различными, если принять во внимание их выпуклость.

Самый большой вопрос

Любознательные математики, конечно же не могли пропустить вопрос:

Сколько бывает различных типов замкнутых выпуклых кривых на сфере?

Более того, для математиков он оказался значительно более важным, чем вопрос о кривых без условия выпуклости. Интерес к нему и различным его обобщениям неожиданно подскочил за последние два года...

Требование выпуклости очень существенно и полностью меняет ответ. Удивительно, однако, не это, а то, что ответ этот был получен лишь двадцать лет тому назад.

Теорема. Существует ровно три различных типа замкнутых выпуклых кривых на сфере (рис. 10).

Рис. 10.

Этот красивый результат был опубликован американским математиком Дж. Литтлом в 1970 году в журнале по дифференциальной геометрии. Остается загадкой как этот интересный геометрический вопрос мог укрыться от внимания классиков еще в прошлом веке.

Сравним рисунки 10 и 6. На первый взгляд, к кривым а) и б) добавилась дополнительная кривая в). Мы увидим, что в действительности кривая а) «отщепилась» от других кривых с нечетным числом оборотов в важный самостоятельный класс.

Кривую а) нельзя перетянуть в кривую с точками самопересечения, любой экватор пересекает ее не более двух раз.

Прежде чем серьезно браться за доказательство, поговорим немного о мотивировках. Почему полезно изучать выпуклые кривые? Во-первых, рассматриваемый нами вопрос — один из тех редких геометрических вопросов, которые благодаря своей простоте и наглядности превращают математику в красивую науку, и этого вполне достаточно для того, чтобы он был интересен сам по себе. Во-вторых, кривая — простейший геометрический объект, связанный со многими другими важными математическими понятиями. Поэтому любой разумный вопрос о кривых должен иметь те или иные приложения. Именно так обстоит дело и с вопросом о выпуклых кривых на сфере.

Мультфильм Литтла

Может ли мультфильм быть доказательством математической теоремы? Не верите — смотрите сами (рис.11). На ваших глазах кривая, совершающая 4 оборота, превращается в кривую б) на рис.9 с числом оборотов 2, оставаясь по дороге выпуклой в каждой точке. Тем, кому мультфильм кажется недостаточно убедительным, не остается ничего другого, как последовать совету Феликса Клейна и сделать гипсовую модель, но при этом доказательство станет гораздо тяжелее (во всяком случае — по весу). Мультфильм — основное и вместе с тем самое красивое место в доказательстве теоремы Литтла- Теперь, дорисовав несколько петелек, каждый сам сможем продеформирсвать кривую с большим числом оборотов в кривую б) или в) в зависимости от четности этого числа.

Итак, любую выпуклую кривую на сфере можно продеформировать в одну из трех кривых на рисунке 9. Кривые а) и б), а также б) и в) принадлежат к различным типам даже без условия гладкости. Нам остается до-казать, что кривую в) нельзя перетянуть в кривую а).

Рис. 11.

Что же мешает кривой в) «обернуться« вокруг сферы, потерять 2 оборота и превратиться в а)? В самом деле, это уже происходило на рисунке 5 (кривая в) перешла в кривую а), но при этом у нее сначала возникли, а затем пропали две точки перегиба). Чтобы убедиться, что дело здесь не в дефекте мультфильма и кривые а) и в) действительно различны как выпуклые кривые, проще всего начать с кривой а), а не с в).

Выпуклая несамопересекающаяся кривая на сфере лежит на полусфере, т. Е. целиком по одну стирону от некоторого экватора.

Это простое утверждение было доказано еще в 20-х годах. Прежде всего поясним его смысл. Утверждение означает, что кривая а) лежит на некоторой полусфере. Такая кривая ничем не отличается от кривой на плоскости.

Рис. 12

Действительно, существует простой способ переделать кривую на полусфере в плоскую — спроецировать ее из центра сферы на плоскость (рис.12). При этом, в отличие от стереографической проекции, диаметры (точнее — полудиаметры, принадлежащие полусфере) переходят в прямые на плоскости. Поэтому выпуклая кривая на полусфере переходит в выпуклую кривую на плоскости. Кривая а) на рисунке 10 при любой деформации вынуждена оставаться на полусфере (неважно, что полусфера может меняться; при этом точка приложения плоскости, на которую происходит проекция, «прокатывается» по сфере). Кривая на плоскости не может перейти в кривую с большим числом оборотов Поэтому кривая а) не может перейти в кривую в).

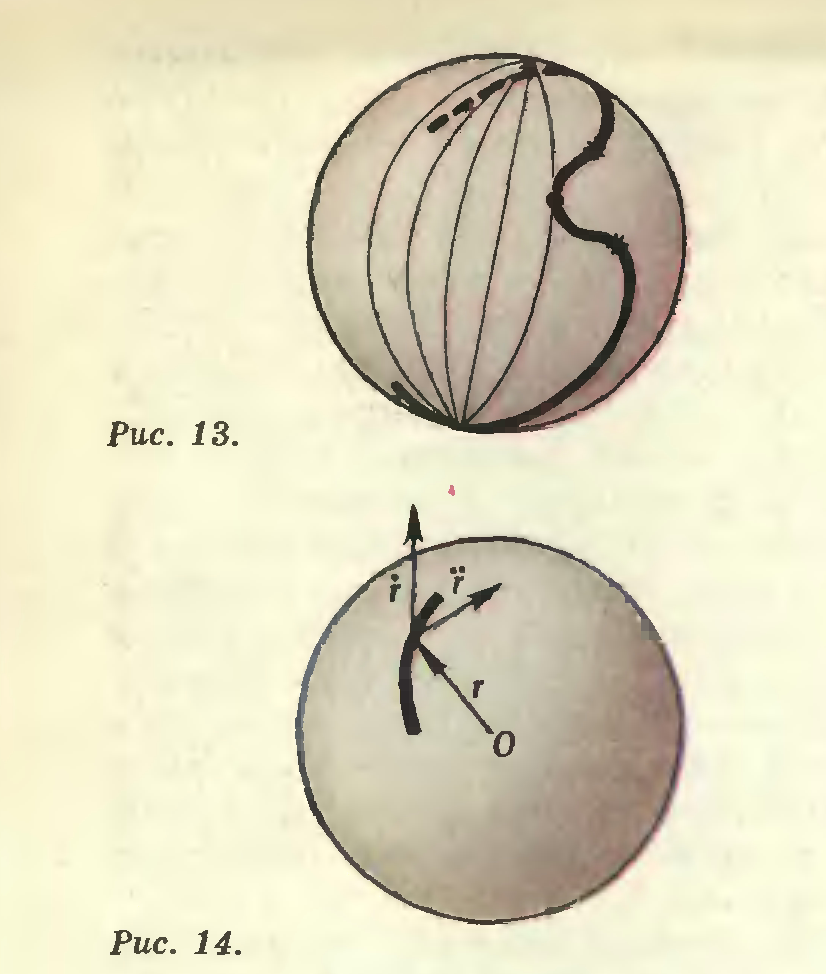
Для доказательства утверждения проведем касательный экватор к любой точке кривой. Выпуклая кривая без самопересечений не может пересекать этот экватор в другой точке (и, стало быть, лежит по отношению к нему на одной из полусфер). В самом деле, если допустить такое пересечение, то на кривой найдется точка, в которой кривая выпукла в противоположную сторону (рис. 13). Значит, у кривой есть и пара перегибов.

Доказательство теоремы Литтла закончено.

Рис. 13, 14.