Сколько на земле кривых (деформации кривых)

Содержание

1). Типы кривых с.3-4.

2). Число оборотов с.4-6.

3). Выпуклость с.6-7.

4). Самый большой вопрос с.7.

5). Мультфильм Литтла с.8-10.

6). Кривые и уравнения с.11.

7). Примеры с. 12.

8). Список литературы с.13

Сколько на земле кривых?

Этот вопрос кажется странным. Можно нарисовать неописуемой множество разнообразных кривых. Договоримся сначала, какие мы будем рассматривать. Здесь нам должен помочь повседневный опыт. Хорошая упругая верёвка или проволока не имеет острых углов. Поэтому мы будем изучать только гладкие кривые (без каких бы то ни было изломов), начерченные на земной поверхности. Таким кривым разрешается иметь сколько угодно точек самопересечения.

Гладких кривых тоже слишком много. Пересчитать их все невозможно. Единственный способ разобраться в нашем вопросе – условиться считать одинаковыми кривые, которые «не очень сильно» отличаются друг от друга.

Типы кривых

Кривая – популярный математический объект, имеющий много интересных характеристик: кривизну, длину, число точек самопересечения, перегиба и т. Д. Все они заслуживают изучения. (О некоторых из них рассказано в статье Табачникова «О плоских кривых» в «Кванте» №11 за 1988 г.) А какие важны для нас? Может быть длина? Но кривых одинаковой длины всё равно слишком много. Считать одинаковыми кривые, у которых одинаковая кривизна? Тогда различных кривых будет больше, чем функций, - многовато… Чтобы больше не гадать, забудем сразу обо всех характеристиках кривой.

Будем понимать выражение «кривые не сильно отличаются друг от друга буквально и считать одинаковыми кривые, которые отличаются «малым шевелением». Теперь нам придется считать одинаковыми любые две кривые, которые можно продеформировать (перетянуть) друг в друга так, чтобы они все время оставались гладкими (рис. 1). Ведь такую деформацию можно разбить на серию «малых шевелений». Будем называть такие кривые кривыми одного типа.

Мы отбросили все видимые различия между кривыми. Естественно предположить, что при таком наивном соглашении все кривые — одного типа. Для незамкнутых кривых так оно и есть. Представим себе лежащую на земле веревку, начинающую распрямляться с одного из концов. Такая веревка плавно развернется в прямую линию (рис. 2). Итак, интересно рассматривать только замкнутые кривые.

Теперь все готово, чтобы сформулировать строгий математический вопрос:

Сколько на Земле различных типов замкнутых кривых?

Этот вопрос имеет много разновидностей и дополнений, приводящие нас в вссьма популярную область современной математики. Об этом речь впереди, а пока давайте считать Землю плоской.

Рис. 1. Рис. 2.

Рис. 3.

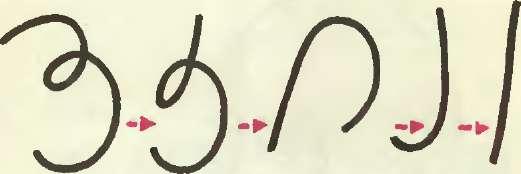
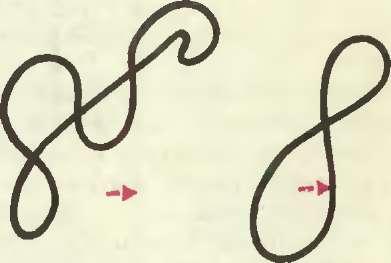
Чиcло оборотов

Попробуйте продеформировать «восьмёрку» в нолик». Получилось? Тогда по дороге у вас обязательно возникло острие (рис, 3). А можно ли продеформировать так, чтобы кривая оставалась гладкой? Похоже, что нельзя. Как это строго доказать? Первая мысль — посчитать число самопересечений кривой или число областей, на которые кривая делит плоскость. Но эти числа могут меняться. Мы уже видели на рисунке 1, как кривая типа «восьмерки» потеряла пару точек самопересечения. Это значит, что четность числа самопересечений осталась без изменения. (Правда, в первый момент две точки превратились в одну, но ее следует рассматривать как слившуюся пару.) Точно так же обстоит дело с числом областей: они образуются и исчезают парами. Итак, «восьмерка» и «нолик» относятся к разным типам. Может быть, существует только два типа кривых? Ничего подобного.

На плоскости существует бесконечно много различных типов замкнутых кривых.

Чтобы доказать эту нашу первую теорему, каждой замкнутой кривой на плоскости поставим в соответствие натуральное число. Рассмотрим точку, движущуюся вдоль кривой (вектор ее скорости касается кривой в каждый момент времени). Пусть за некоторое время точка обежит всю кривую и вернется в начальное положение.

Рис. 4.

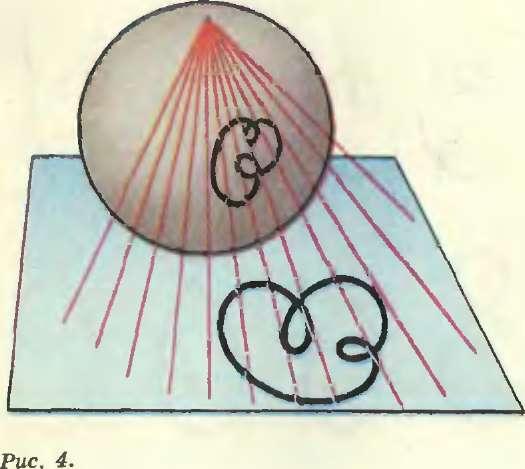
Рис. 5.

Числом оборотов кривой мы будем называть число полных оборотов, которые совершает вектор скорости этой точки. (Неважно, в каком направлении поворачивается вектор. Это зависит от направления движения точки вдоль кривой.)

Число оборотов — инвариант, т. е. оно не меняется при деформации кривой. Ведь это число не может измениться скачком при «малом шевелении» кривой, а деформация — цепочкатаких «шевелений». Следовательно, кривые с разным числом оборотов относятся к разным типам.

Разных чисел бесконечно много, значит, и кривых — тоже. Теорема доказана.

На самом деле, число оборотов — единственный инвариант плоской кривой. Это значит, что две кривые с одинаковыми числами оборотов принадлежат к одному типу. Попробуйте сами придумать доказательство, а если не получится — поэкспериментируйте. В крайнем случае, прочтите «Квант» № 4 за 1983 г. А мы лучше вспомним, что Земля — шар.

И все-таки она вертится...

Поверхность Земли — сфера. Сколько же на ней кривых? Сфера — это плоскость плюс еще одна точка (рис. 4). Рисунок 4 называется стереографической проекцией. Сделаем стереографическую проекцию из точки, не лежащей на кривой. Тогда эта кривая попадет на плоскость. Значит» на сфере столько же типов кривых, сколько на плоскости? Да, недалеко мы ушли от тех, кто и в правду считает Землю плоской. Вот правильный ответ.

На сфере существует ровно два различных типа замкнутых кривых.

Доказательство качнем с картинки (рис. 5). Как видите, число оборотов больше не сохраняется. Вот, что отличает кривые на сфере от кривых на плоскости. «Обернувшись» вокруг сферы, кривая потеряла два оборота. Теперь легко проделать такую же операцию над кривой с любым числом оборотов (надо только дорисовать у кривых на рисунке 5 несколько петелек в любом месте). Мы получили, что любую кривую можно продеформировать в одну из кривых на рисунке 6. В какую именно — зависит от четности числа оборотов.

Рис. 6.

Но как доказать, что кривые а) и 6) — разных типов не только на плоскости, но и на сфере? Ведь, строго говоря, число оборотов в этом случае вообще не определено. Выручает уже знакомая нам четность числа самопересечении. У кривой б) это число нечетно, а у кривой а) — четко (равно нулю).