Lektsii_Rubleva_1 / Гл 02 Пох_дна / Пар 2-04 Теореми про середнє

7

Глава 2

Похідна

4. Теореми про середнє

Функція має в точці локальний максимум (мінімум), якщо : . Якщо при цьому виконується нерівність , то максимум (мінімум) називається строгим, інакше – нестрогим. Локальні максимуми та мінімуми називаються екстремумами.

Теорема 1.	(Ферма)
	Нехай і - внутрішня точка множини . Якщо функція набуває в точці найбільшого або найменшого значення і диференційована в ній, то .

Доведення. З означення диференційованої функції в точці можемо записати рівність: , де - неперервна в точці . Припустимо, що , із властивості стійкості нерівності : - зберігає знак. Якщо - екстремальна точка ліва частина останньої нерівності в околі зберігає знак, а права частина змінює цей знак – суперечність .

Теорему доведено.

Теорема 2.	(Ролля)
	Нехай , диференційована в кожній точці . Якщо , то : .

Доведення. Якщо , то твердження очевидне. Якщо , то, за теоремою Вейєрштрасса, вона набуває найбільшого та найменшого значень на , які не співпадають. Одне з цих значень досягається в деякій середній точці , тоді, за теоремою Ферма, .

Теорему доведено.

Наслідок.	(Узагальнення теореми Ролля).
	Нехай , диференційована в кожній точці . Якщо , то : .

Доведення. Якщо , то знов все очевидно. Якщо , то достатньо розглянути функцію , де . Тоді і можна застосувати для теорему Ролля : .

Розглянемо випадок , . (Решта випадків – аналогічно). Так як : , припустимо, що . Розглянемо число , з того, що : , і : на і на : (за теоремою Коші) за теоремою Ролля для на : .

Теорему доведено.

Приклад 1.	Якщо має похідну в кожній точці , , то рівняння має принаймні один розв’язок на .
	Розглянемо функцію . Тоді і вона задовольняє теорему Ролля : , з того, що : .
Приклад 2.	Якщо многочлен -го степеня не має комплексних коренів (тобто, з урахуванням кратності він має рівно дійсних коренів), то всі його похідні теж мають лише дійсні корені.
	Якщо - корінь кратності , то похідна має цей корінь кратності . Крім того, якщо - сусідні корені многочлена , то : . Тобто, якщо має різних коренів, то похідна має різний корінь. Залишилося обчислити кількість коренів похідної від многочлена , кількість коренів складає: .

Теорема 3.	(Дарбу)
	Якщо диференційована в кожній точці : , то : .

Доведення. За теоремою Вейєрштрасса на набуває найбільшого та найменшого значень. Якщо принаймні одне з них досягається в точці , то, за теоремою Ферма, . Покажемо, що інше не можливо, тобто екстремуми не можуть досягатися на краях. Якщо припустити, що, , 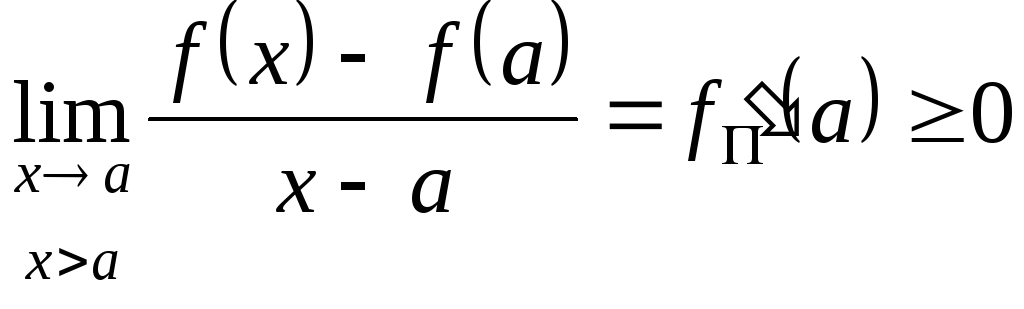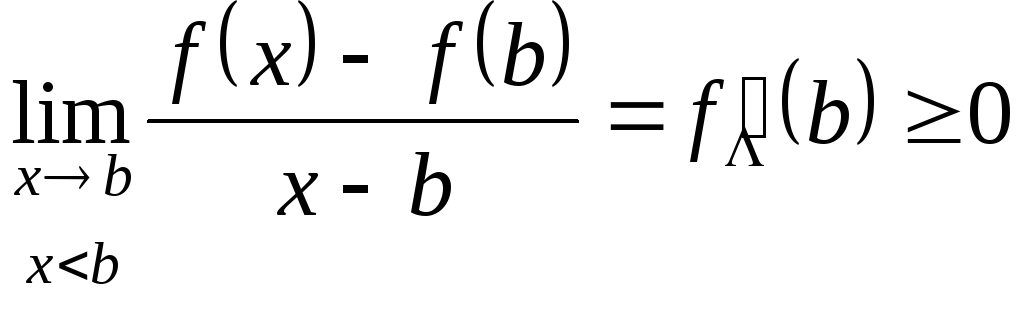і умова не виконується.

Аналогічно, коли , .

Наслідок 1.	(Про проміжні значення похідної).
	Якщо диференційована на , то її похідна набуває усіх проміжних значень між і .

Доведення. Нехай довільне дійсне число між і . Розглянемо функцію : , тоді : .

Наслідок доведено.

Наслідок 2.	(Про збереження знаку похідною).
	Якщо диференційована на і , то зберігає цілком певний знак на .

Доведення. Якщо : : - суперечність.

Наслідок доведено.

Теорема 4.	(Лагранжа)
	Нехай функція неперервна на , диференційована в кожній точці . Тоді :
		(1)

Доведення. Нехай , тоді розглянемо функцію , . ;

за теоремою Ролля : .

Теорема доведена.

Запишемо цю формулу трохи інакше: зрозуміло, що ; тому можна покласти , . Тоді, якщо , і на цьому проміжку задовольняє умову теореми Лагранжа останню формулу можна записати у вигляді:

, , (2)

яка називається формулою скінчених приростів Лагранжа.

Приклад 3.	Довести нерівність
	.

Формулу (1) можна узагальнити таким чином:

.

Теорема 5.	(Узагальнення теореми Лагранжа)
	Нехай функція неперервна на і має праву похідну у кожній точці , за винятком, можливо, деякої її зліченої підмножини . Якщо , то .

Доведення. Нехай перенумеровані члени множини , при цьому, якщо , то . Зафіксуємо довільне , і розглянемо множину таких точок з , що виконується нерівність:

(3)

(Під слід розуміти просто суму, якщо кількість індексів , для яких скінчене, і 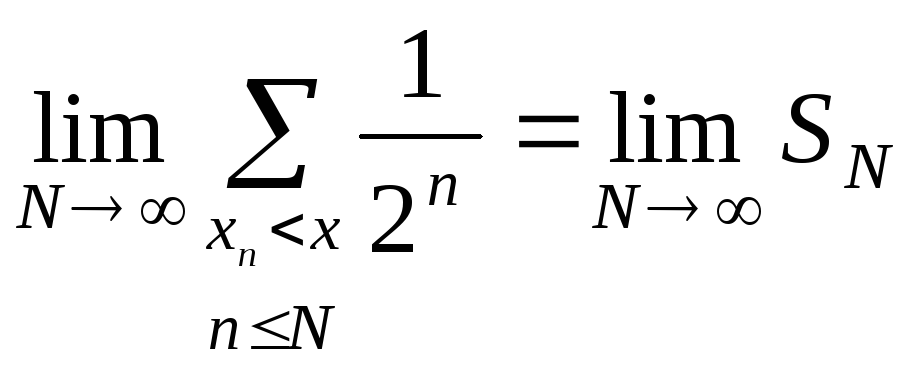, яка існує і скінчена, в наслідок того, що - не спадна і обмежена числом ). Очевидно, що . Покажемо, що до входять також і числа, більші за .

1) Якщо існує , то з диференційованості в точці маємо: : виконується і нерівність (3) для будь-якої точки проміжку .

2) Якщо , тобто не існує, то з неперервності в точці можемо записати: : , тому що . Таким чином точка .

Тобто множина містить і внутрішні точки сегменту , внаслідок обмеженості множини (точкою ) . Покажемо, що . З означення верхньої межі : з визначення множини . З неперервності на зробимо граничний перехід при

, (4)

звідки слідує, що .

Тепер покажемо, що .

1) Якщо і і , і виконується: . Додавши до останньої нерівності (4), одержимо: