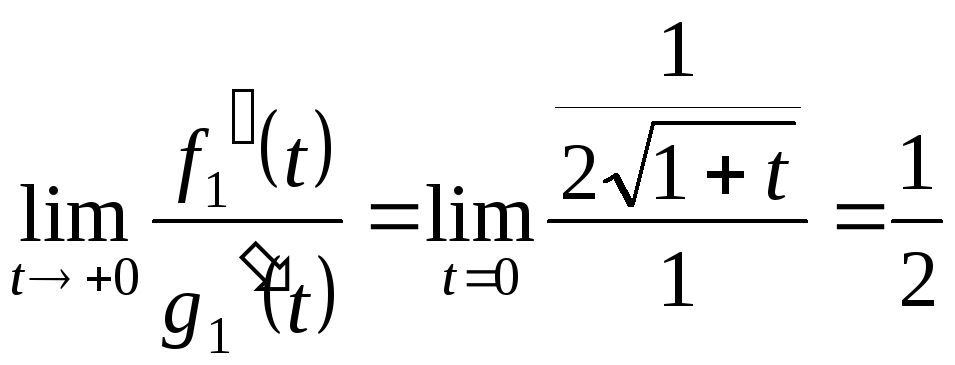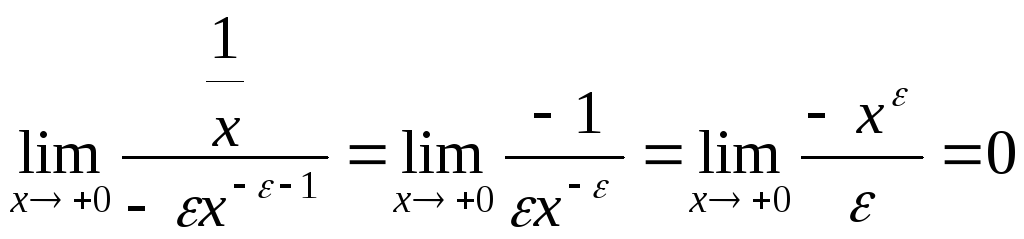Lektsii_Rubleva_1 / Гл 02 Пох_дна / Пар 2-05 Правила Лоп_таля
.doc
Глава 2
Похідна
5. Правила Лопіталя
|
Теорема 1. |
(Правило
Лопіталя для невизначеностей типу
|
|
|
Нехай
функції
|
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
Доведення.
Розглянемо розширення функції на
півінтервал
![]() ,
доповнивши їх нулями в точці
,
доповнивши їх нулями в точці
![]() .
Виберемо довільну
.
Виберемо довільну
![]() :
:
![]() .
З формули Коші для скінчених приростів
(або з наслідків)
.
З формули Коші для скінчених приростів
(або з наслідків)
![]() :
:


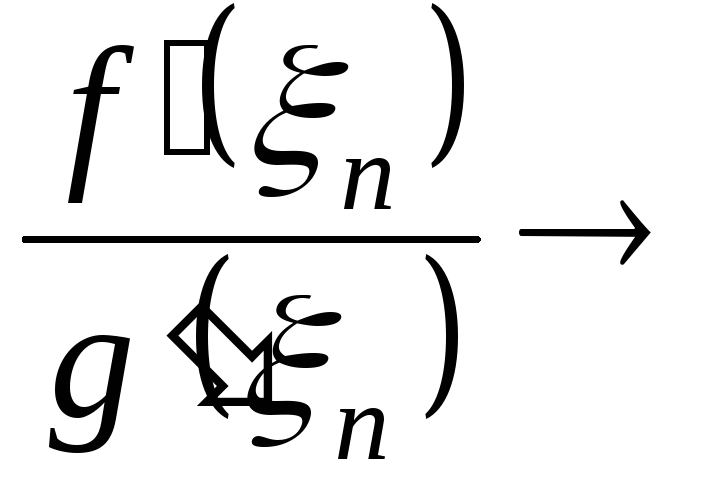
![]() ,
бо
,
бо
![]() і
і
![]()
![]() за означенням Гейне ми одержимо, що
за означенням Гейне ми одержимо, що
![]() .
.
Теорему доведено.
|
Приклад 1. |
|
|
|
Маємо
невизначеність
|
Зауважимо, що в зворотній бік теорема місця не має.
|
Приклад 2. |
|
Наслідок 1. |
(Перше
правило Лопіталя для
|
|
Якщо
для функцій
|
|
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
Доведення.
Доведення полягає в використанні правила
Лопіталя
![]() разів по черзі для пар функцій (
разів по черзі для пар функцій (![]() ,
,![]() ),
(
),
(![]() ,
,![]() ),…,(
),…,(![]() ,
,
![]() ).
).
Доведення завершене.
Наслідок 2. |
(Перше правило Лопіталя на нескінченності) |
|
Якщо
|
|
1) |
|
2) |
|
3) |
|
4) |
|
Доведення.
Розглянемо функції
![]() ,
,
![]() ,
,
![]() .
Тоді при
.
Тоді при
![]()
![]() .
За умовою існує:
.
За умовою існує:
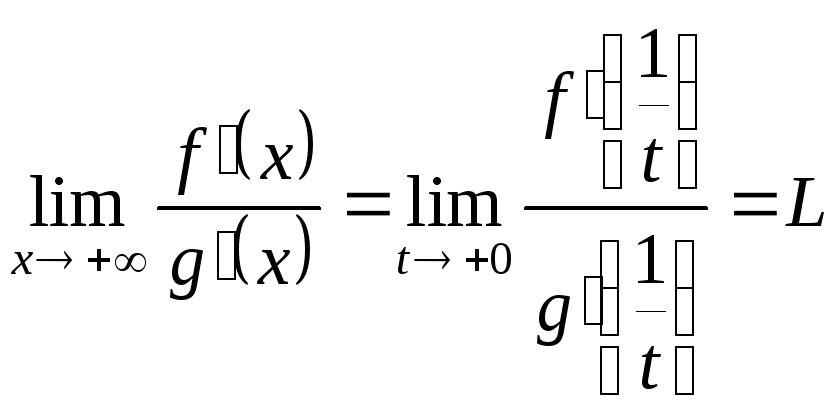
![]()
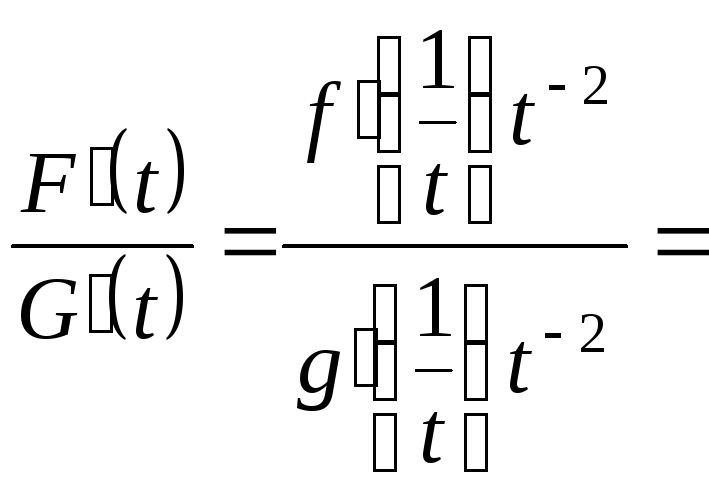
 при
при
![]()
![]()
![]()
![]() .
.
Доведення завершене.
|
Приклад 3. |
|
|
|
|
|
Теорема 2. |
(Правило
Лопіталя для невизначеностей типу
|
|
|
Нехай
|
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
Доведення.
Нехай
![]() - довільна
послідовність, що збігається до
- довільна
послідовність, що збігається до
![]() .
Нехай
.
Нехай
![]() - два
елемента послідовності з достатньо
великими номерами
- два
елемента послідовності з достатньо
великими номерами
![]() .
З теореми Коші
.
З теореми Коші
![]() :
:

![]()
 .
З умови
.
З умови
![]() при
при
![]() слідує, що
слідує, що
![]()
![]()
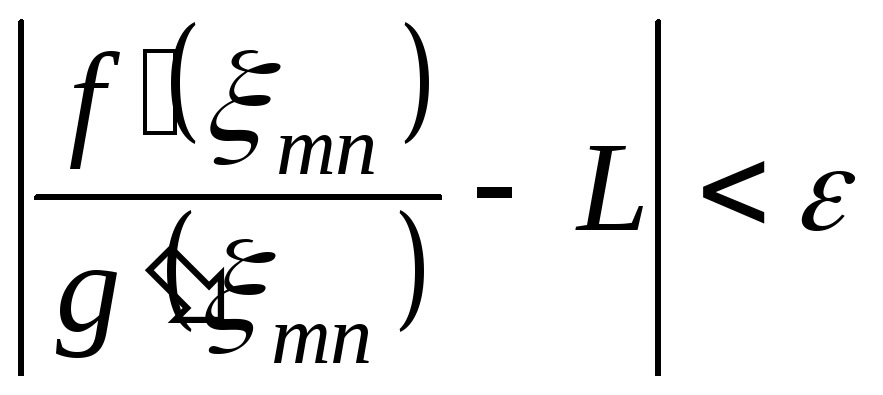 .
.
При
фіксованому
![]()
![]()
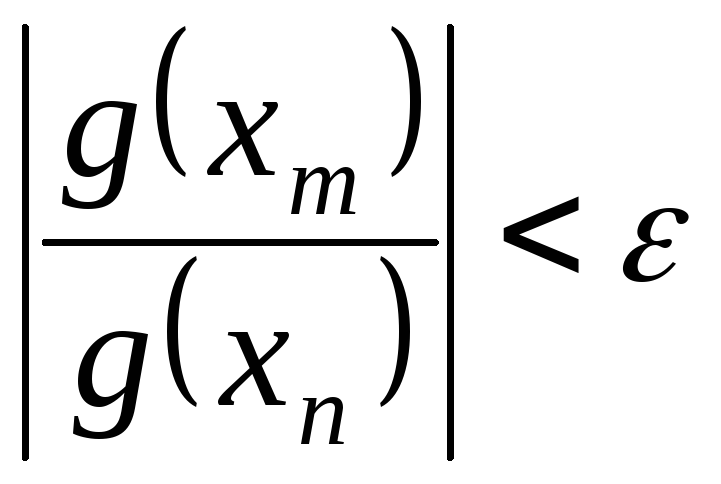
![]()

 ;
;
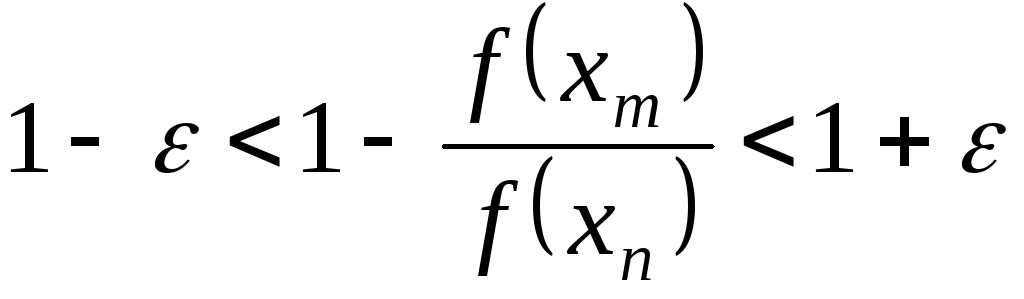
![]()
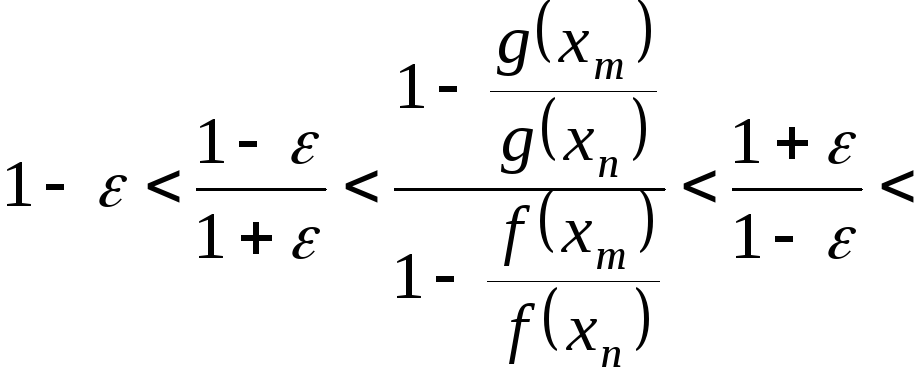
![]() ,
при достатньо малих
,
при достатньо малих
![]()
![]()
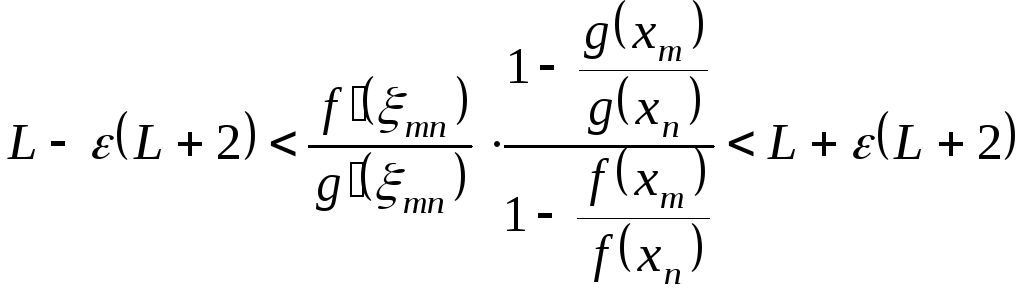
![]()

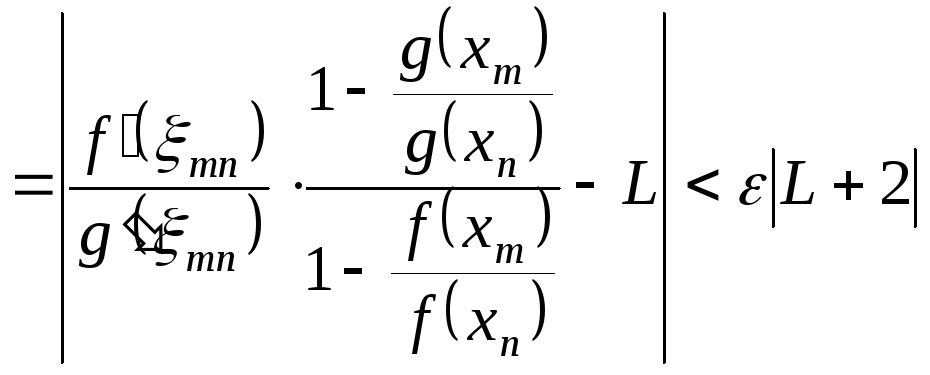
![]()
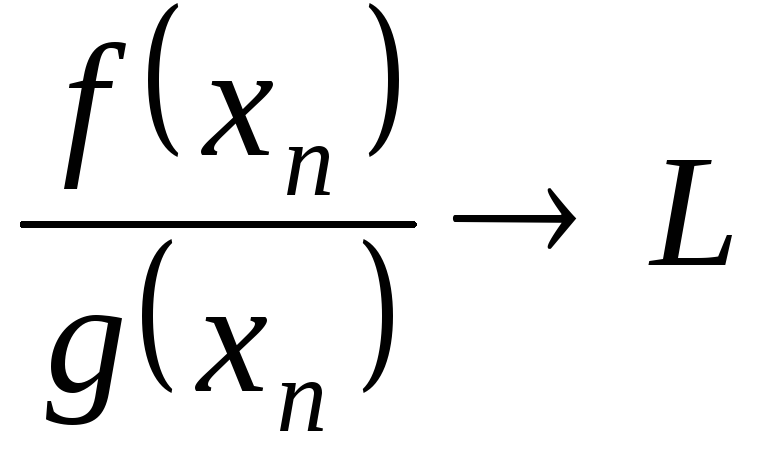 ,
за означенням Гейне
,
за означенням Гейне
![]() .
.
Теорема доведена.
|
Приклад 4. |
|
|
|
Маємо
невизначеність
|
Наслідок 1. |
(Друге
правило Лопіталя для
|
|
Якщо
функції
|
|
1) |
|
2) |
|
3) |
|
4) |
|
Наслідок 2. |
(Друге правило Лопіталя на нескінченності) |
|
Теорема
залишається чинною, якщо
|
Доведення цих наслідків проводиться аналогічно до доведення попередніх наслідків. Першій методом математичної індукції, а другий – заміною змінної.
|
Приклад 5. |
Знайти
|
|
Використаємо
правило Лопіталя
|

 наша
границя теж дорівнює
наша
границя теж дорівнює