
Lektsii_Rubleva_1 / Гл 02 Пох_дна / Пар 2-01 Визначення пох_дної - копия
.doc
Глава 2
Похідна
1. Визначення похідної, правила диференціювання
Нехай
функція
![]() ,
,
![]() .
Функція
.
Функція
![]() називається диференційованою
в точці
називається диференційованою
в точці
![]() ,
якщо існує така неперервна в точці
,
якщо існує така неперервна в точці
![]() функція
функція
![]() ,
що
,
що
![]() виконується рівність :
виконується рівність :
![]() (1)
(1)
Якщо
![]() - гранична точка множини
- гранична точка множини
![]() ,
то число
,
то число
![]() називається похідною
функції
називається похідною
функції
![]() в точці
в точці
![]() і позначається символом
і позначається символом
![]()
![]() .
.
Приклад 1. |
Розглянемо
функції
|
|
|
|
|
|
|
|
Теорема 1. |
(Обчислення похідної). |
|
|
|
Нехай
|
|
|
|
|
(2) |
Доведення. Безпосередній наслідок формули (1).
|
Наслідок. |
(Необхідна умова диференційованості). |
|
|
Якщо
функція
|
|
Приклад 2. |
Знайти
похідні в точці
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 2. |
(Про похідну композиції) |
|
|
|
Нехай
функція
|
|
|
|
(3) |
|
Доведення.
За означенням диференційованості
![]() в точці
в точці
![]() ,
існує неперервна в точці
,
існує неперервна в точці
![]() функція
функція
![]() ,
,
![]() ,
така що
,
така що
![]() :
:
![]() .
Нехай
.
Нехай
![]()
![]()
![]()
![]()
![]()
![]() .
З диференційованості
.
З диференційованості
![]() ми одержимо, що існує неперервна в точці
ми одержимо, що існує неперервна в точці
![]() функція
функція
![]() :
:
![]() виконується рівність:
виконується рівність:
![]() .
Підставивши це в останню рівність,
одержимо:
.
Підставивши це в останню рівність,
одержимо:
![]() ,
з чого слідує диференційованість
композиції та рівність (3).
,
з чого слідує диференційованість
композиції та рівність (3).
Приклад 3. |
|
Теорема 3. |
(Лінійність диференціювання) |
Нехай
функції
|
|
Доведення.
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
Теорема доведена.
Теорема 4. |
(Похідна добутку в нулі функції) |
|
Нехай
|
||
|
|
||
|
|
|
(4) |
Доведення.
З диференційованості
![]() в точці
в точці
![]() ,
маємо рівність:
,
маємо рівність:
![]() ,
де
,
де
![]() - неперервна в точці
- неперервна в точці
![]()
![]()
![]()
![]()
![]() .
.
Теорема доведена.
|
Наслідок. |
(Диференціювання добутку функцій) |
|
|
|
Якщо
функції
|
|
|
|
||
|
|
|
(5) |
Доведення
випливає з тотожності:
![]() і теорем 3,4.
і теорем 3,4.
Наслідок доведення.
Теорема 5. |
(Похідна частки) |
|
Нехай
|
||
|
|
|
(6) |
Доведення. Скористаймося правилом диференціювання добутку та похідною композиції функцій:
![]()
![]()

![]()
 .
.
Теорему доведено.
Теорема 6. |
(Похідна оберненої функції) |
|
Нехай
функція
|
||
|
|
||
|
|
|
(7) |
Доведення.
З означеності диференційованості
функції
![]() в точці
в точці
![]() існує неперервна в цій точці функція
існує неперервна в цій точці функція
![]() :
:
![]() :
:
![]() ,
з взаємної однозначності
,
з взаємної однозначності
![]() слідує, що
слідує, що
![]() при
при
![]() ,
і
,
і
![]() ,
якщо покласти
,
якщо покласти
![]() ,
одержимо:
,
одержимо:
![]() .
Функція
.
Функція
![]() неперервна в точці
неперервна в точці
![]()
![]()
![]() диференційована в точці
диференційована в точці
![]() .
Якщо
.
Якщо
![]() - гранична точка множини
- гранична точка множини
![]() ,
то, згідно означення похідної, маємо:
,
то, згідно означення похідної, маємо:
![]() .
.
Приклад 4. |
Знайти
|
|
Враховуючи правила диференціювання елементарних функцій, одержимо таблицю похідних:
|
1) |
|
7) |
|
|
2) |
|
8) |
|
|
3) |
|
9) |
|
|
4) |
|
10) |
|
|
5) |
|
11) |
|
|
6) |
|
12) |
|
Приклад 5. |
Знайдемо похідну степенево-показникової функції: |
|
|
Якщо
функція
![]() диференційована в кожній точці деякої
множини
диференційована в кожній точці деякої
множини
![]() ,
то вона називається диференційованою
на множині
,
то вона називається диференційованою
на множині
![]() .
.



 ;
;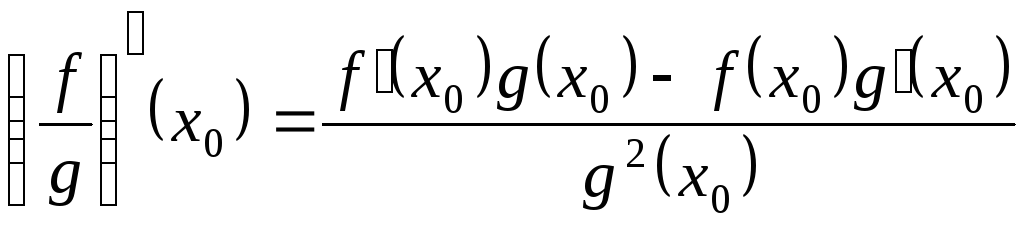 .
.