Lektsii_Rubleva_1 / Гл 02 Пох_дна / Пар 2-02 Односторонн_ пох_дн_ Диференц_ал
.doc
Глава 2
Похідна
2. Односторонні похідні, диференціал
Нехай
![]() .
Якщо
.
Якщо
![]() - гранична точка множини
- гранична точка множини
![]()
![]() ,
то
,
то
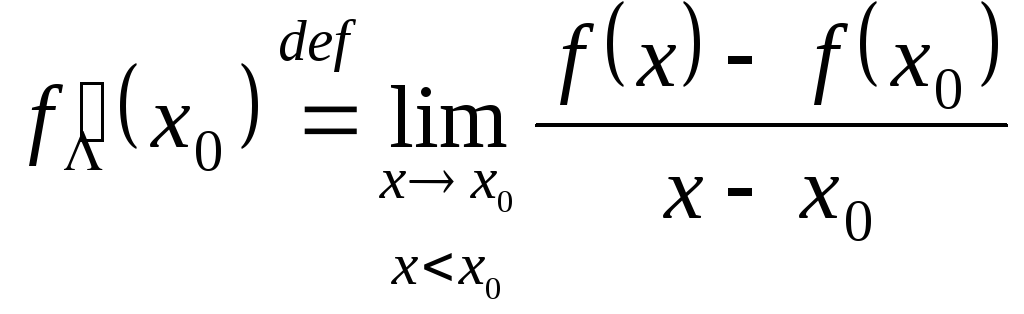
 .
Числа
.
Числа
![]() та
та
![]() ,
якщо вони існують, називаються відповідно
лівою
та правою
похідними функції
,
якщо вони існують, називаються відповідно
лівою
та правою
похідними функції
![]() у точці
у точці
![]() .
.
|
Теорема 1. |
(Критерій диференційованості функції) |
|
|
Для
того, щоб неперервна функція
|
Доведення.
Згідно теореми про існування границі
функції в точці для функції
![]() ,
,
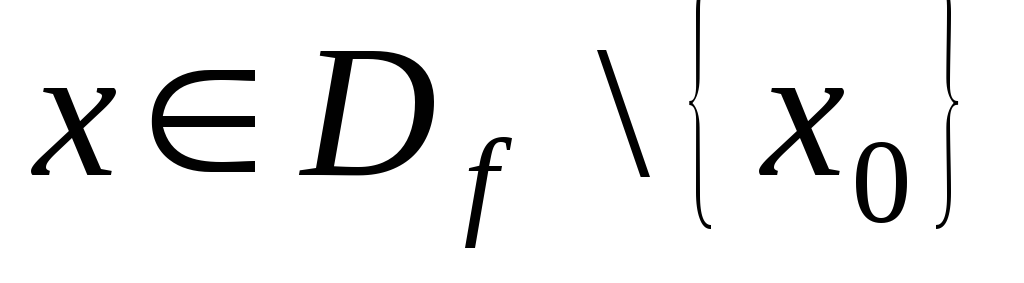 ,
можемо сказати, що
,
можемо сказати, що
![]() має скінчену границю в точці
має скінчену границю в точці
![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]()
![]() ,
але ж
,
але ж
![]() ,
,
![]() .
.
Теорему доведено.
|
Приклад 1. |
|
|
|
|
Для
функції
![]() виберемо дві довільні точки
виберемо дві довільні точки
![]() та
та
![]() з
з
![]() .
Різницю
.
Різницю
![]() називають приростом
функції
називають приростом
функції
![]() в точці
в точці
![]() ,
відповідним приросту незалежної змінної
,
відповідним приросту незалежної змінної
![]() ,
і позначають через
,
і позначають через
![]() .
Якщо
.
Якщо
![]() - диференційована в точці
- диференційована в точці
![]() функція, граничній для множини
функція, граничній для множини
![]() ,
то формулу для її приросту можна надати
у вигляді:
,
то формулу для її приросту можна надати
у вигляді:
![]() , (1)
, (1)
де
![]() - неперервна в точці
- неперервна в точці
![]() функція, і
функція, і
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() ,
тоді рівність (1)
можна переписати у вигляді:
,
тоді рівність (1)
можна переписати у вигляді:
![]() (2)
(2)
Відображення
![]() називається лінійним,
якщо
називається лінійним,
якщо
![]() виконуються умови:
виконуються умови:
1)
![]() ,
,
![]() (адитивність);
(адитивність);
2)
![]() ,
,
![]() (однорідність).
(однорідність).
|
Лема 1. |
(Загальний вигляд лінійного відображення) |
|
|
Загальний
вигляд лінійного відображення з
|
Доведення.
Позначимо
![]() .
Легко зрозуміти, що відображення
.
Легко зрозуміти, що відображення
![]() є лінійним. Тепер треба показати, що
будь-яке інше лінійне відображення має
такий самий вигляд. Дійсно:
є лінійним. Тепер треба показати, що
будь-яке інше лінійне відображення має
такий самий вигляд. Дійсно:
![]() .
.
Лема доведена.
|
Теорема 2. |
(Приріст диференційованої функції). |
|
|
|
Нехай
|
|
|
|
|
(3) |
|
|
то
функція
|
|
Доведення.
З рівності (3)
маємо
![]() .
.
Теорему доведено.
Якщо
функція
![]() диференційована в точці
диференційована в точці
![]() ,
граничній для множини
,
граничній для множини
![]() ,
то лінійна функція
,
то лінійна функція
![]() ,
яка задовольняє умову (3),
називається диференціалом
функції
,
яка задовольняє умову (3),
називається диференціалом
функції
![]() у точці
у точці
![]() і позначається символом
і позначається символом
![]() .
Для будь-якого
.
Для будь-якого
![]() вона набуває значення
вона набуває значення
![]() . (4)
. (4)
Таким
чином, приріст функції
![]() ,
диференційованої в точці
,
диференційованої в точці
![]() ,
граничній для
,
граничній для
![]() ,
складається з суми двох доданків, перший
з них значення диференціала
,
складається з суми двох доданків, перший
з них значення диференціала
![]() при
при
![]() ,
а другий є функцією вигляду:
,
а другий є функцією вигляду:
![]()
![]() ,
де
,
де
![]() - неперервна в точці
- неперервна в точці
![]() функція, що в точці
функція, що в точці
![]() дорівнює нулеві.
дорівнює нулеві.
Розглянемо
функцію
![]()
![]() .
Тоді
.
Тоді
![]() :
:
![]() . (5)
. (5)
Тобто
диференціали функції
![]() в будь-якій точці рівні між собою, і їх
позначають через
в будь-якій точці рівні між собою, і їх
позначають через
![]() .
Цей диференціал, що не залежить від
.
Цей диференціал, що не залежить від
![]() ,
називають диференціалом незалежної
змінної. З цього можна одержати:
,
називають диференціалом незалежної
змінної. З цього можна одержати:
![]()
![]()
![]()
![]()
![]()
![]() . (6)
. (6)
|
Приклад 2. |
|
|
|
|
Нехай
визначені функції
![]() ,
,
![]() ,
такі, що
,
такі, що
![]() ,
і
,
і
![]() ,
є граничною для цієї множини, і композиція
,
є граничною для цієї множини, і композиція
![]() диференційована в точці
диференційована в точці
![]() .
Тоді її похідна записується у вигляді:
.
Тоді її похідна записується у вигляді:
![]() ,
а диференціал набуває вигляду:
,
а диференціал набуває вигляду:
![]()
![]()
![]() ,
де
,
де
![]() ,
,
![]() .
З останнього співвідношення, а саме
.
З останнього співвідношення, а саме
![]()
![]() - форма диференціала така сама, як і для
випадку незалежної змінної
- форма диференціала така сама, як і для
випадку незалежної змінної
![]() ,
ця властивість називається інваріантність
першого диференціалу.
,
ця властивість називається інваріантність
першого диференціалу.
|
Приклад 3. |
|
|
|
|
|
|
|
|
|
|
|
Приклад 4. |
|
Беручи
до уваги, що з формули (6)
похідну функції
![]() можна розглядати як частку диференціалів
функції та незалежної змінної:
можна розглядати як частку диференціалів
функції та незалежної змінної:
![]() ,
а саму похідну позначити як
,
а саму похідну позначити як
![]() .
.
Для
наближеного обчислення значень
диференційованої функції з деякого
![]() -
околу точки
-
околу точки
![]() при малих
при малих
![]() користуються наближеною формулою:
користуються наближеною формулою:
![]() , (7)
, (7)
тобто
ми відкидаємо нескінченно малу, а
залишаємо лінійну частину доданку. З
формули (7)
одержуємо формулу для наближених
обчислень (![]() ):
):
![]() . (8)
. (8)
|
Приклад 5. |
Знайти
наближено
|
|
|
|
Нехай
функція
![]() задана параметрично, тобто
задана параметрично, тобто
![]() ,
,
![]() ,
,
![]() .
Припустимо, що
.
Припустимо, що
![]()
![]() ,
,
![]() ,
,
![]() і виконані всі умови теореми про
диференціювання функції
і виконані всі умови теореми про
диференціювання функції
![]() як оберненої. Тоді, якщо
як оберненої. Тоді, якщо
![]() ,
,
![]() ,
і для
,
і для
![]() одержимо
правило
диференціювання параметрично заданої
функції:
одержимо
правило
диференціювання параметрично заданої
функції:
![]()
![]()
![]()
![]() (9)
(9)
|
Приклад 6. |
|
|
Приклад 7. |
Неявно
задана функція
|