1.3. Анализ системы

1.3.1. Общие положения

Пакет CONTROLпредоставляет пакет процедур для осуществления анализа САУ, прежде всего, для определения отклика системы на внешние воздействия как во временной, так и в частотной областях.

1.3.1.1. Примеры анализа во временной области

Для нахождения временныхоткликов системы на внешние воздействия некоторых видов предусмотрены функции:

impulse Нахождение отклика на импульсное входное воздействие.

step Нахождение реакции системы на единичный скачок входного воздействия.

initial Определение собственного движения системы при произвольных начальных условиях.

lsim Определение реакции системы на входное воздействие произвольной формы, задаваемое в виде вектора его значений во времени.

1.3.1.2. Примеры анализа в частотной области

Группа процедур для представления реакции системы на гармонические воздействия в частотной области:

bode Строит график АЧХ и ФЧХ (диаграмму Боде) указанной системы.

nyquist Строит в комплексной плоскости график АФХ разомкнутой системы в полярных декартовых координатах.

nichols Строит карту Николса системы, т.е. график АФХ разомкнутой системы в декартовых координатах.

sigma Строит график зависимости от частоты сингулярных значений системы; обычно совпадает с АЧХ системы.

margin Строит диаграмму Боде с указанием запасов по амплитуде и по фазе.

1.3.1.3. Процедуры, вычисляющие отдельные характеристики и графически показывающие расположение полюсов и нулей системы

pole Расчет полюсов системы.

zpkdata Расчет полюсов, нулей и коэффициента передачи системы.

pzmap Построение на комплексной плоскости карты расположения нулей и полюсов системы.

1.3.2. Примеры анализа во временной области

Применяя процедуру stepк созданной в п. 2.2модели,

>> step(sys)

можно получить график

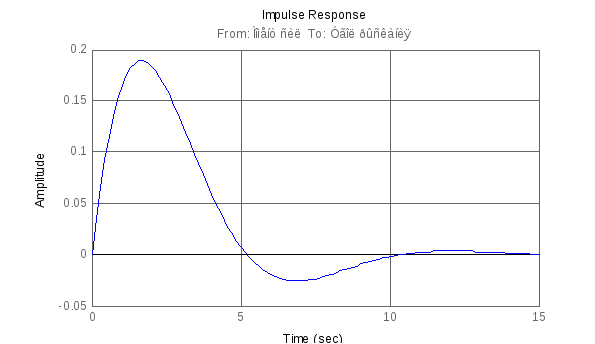
Аналогично, использование процедуры impulse

>> impulse(sys)

приведет к появлению в графическом окне графика, приведенного ниже:

При применении процедуры initial необходимо в число входных параметров включить, во-первых, полный вектор всех начальных условий по переменным состояния, а, во-вторых, момент времени окончания процесса интегрирования.

>> sssys=ss(sys)

>> initial(sssys,[0 0 0 1],20)

Получим

Для применения процедуры lsim необходимо предварительно задать векторtзначений времени, в которых будут заданы значения входного воздействия, а затем задать векторuзначений входной величины в указанные моменты времени

>> t=0:0.01:40; u=sin(t); lsim(sssys,u,t);grid

Результат представлен на следующей фигуре: