П.6.Основные числовые функции и их графики
Основными элементарными функцияминазываются следующие: степенная функция
,
гделюбое
действительное число; показательная
функция
,
гдеа>0,a≠1;
логарифмическая функция
,
гдеа>0,a≠1;
тригонометрические функцииy=sinx,y=cosx,
y=tgx,y=ctgx; обратные тригонометрические функцииy=arcsinx,y=arccosx,y=arctgx,y=arcctgx.
Линейная функция.
Квадратичная функция.
Степенная функция.Область
определения степенной функции
зависит от показателя.
Эта функция при любомaопределена в интервале 0х+,
то есть для всех положительных значенийх. Приaнатуральном областью определения
является вся числовая ось. Множеством
значений функции будет интервал 0у+приaчетном
и промежуток –у+принечетном (рис. 15).
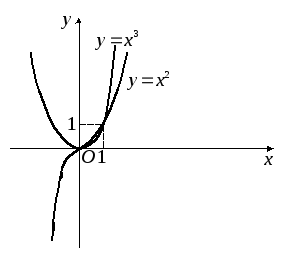
Рис. 15
Показательная функция.Областью
определения показательной функции
является вся числовая ось, то есть
промежуток (–;
+), а множеством
значений функции - промежуток (0; +)
(рис. 16).
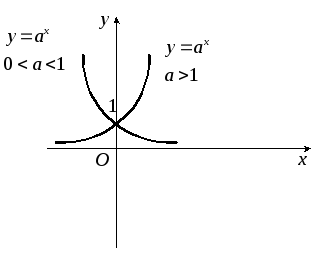
Рис. 16
Логарифмическая функция.Областью
определения логарифмической функции
является промежуток
,
а множеством значений функции - промежуток
(рис. 17).
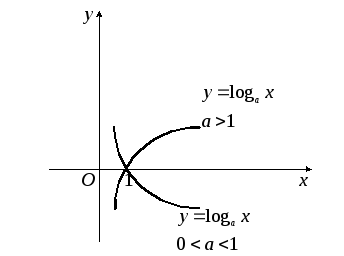
Рис. 17
Тригонометрические функции.Областью определения функцийy=sinxиy=cosxявляется промежуток
,
а множеством значений функций ––
отрезок–1;
1(рис. 18 и 19).
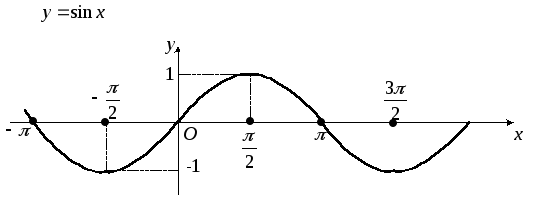
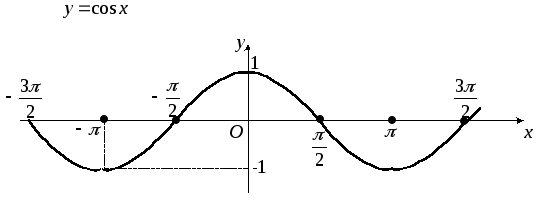
Рис. 18 Рис. 19
Функция
определена на всей числовой оси, кроме
точек
,
т.е. область определения этой функции
есть совокупность интервалов
.
Функция
определена на всей числовой оси, кроме
точек
,
т.е. область определения этой функции
состоит из интервалов
.
Множеством значений функций
и
является промежуток
(рис. 20 и 21).
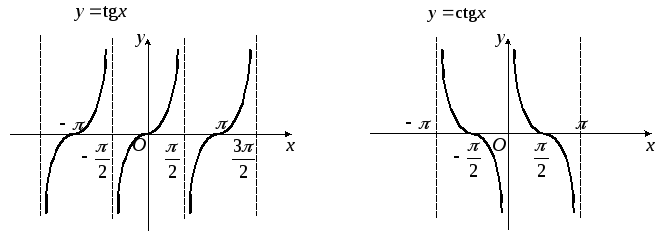
Рис. 20 Рис. 21
Обратные тригонометрические функции.Областью определения функцийy=arcsinxи
y=arccosxявляется отрезок–
1; 1. Множеством
значений функцииy=arcsinxявляется отрезок
,
а функцииy=arccosx–– отрезок
(рис. 22 и 23).
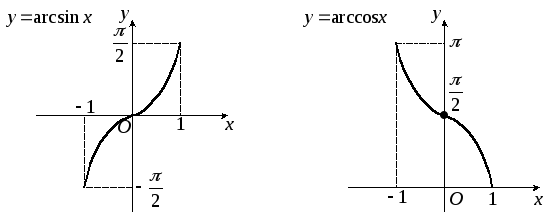
Рис. 22 Рис. 23
Областью определения функций y=arctgxиy=arcсtgxявляется промежуток
.
Множеством значений функцииy=arctgxбудет интервал
,
а функцииy=arcсtgx–– интервал
(рис. 24 и 25).
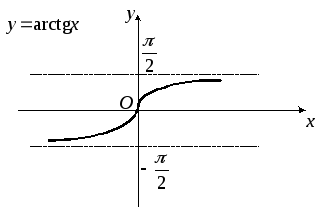
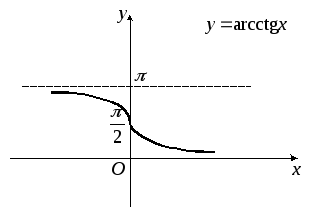
Рис. 24 Рис. 25