19

Глава 1 соответствия. Действительные числа

§ 1. Соответствия между множествами

П.1. Множества и операции над ними

Основными неопределяемыми понятиями математики являются «множество», «элемент множества». Множества представляют собой совокупность каких-либо предметов (объектов), обладающих общим свойством. Эти объекты бывают разной природы: числовые, геометрических фигур, людей и т.д. Договоримся называть их «элементами множества». Множества принято обозначать большими буквами латинского алфавитаА,В, С,…, Х, У, Z, а элементы множеств – маленькими буквами латинского алфавитаa, b, c, …, x, y, z. Если некоторый объектa является элементом некоторого множестваA, то говорят, что «элемент а принадлежит множествуА» и обозначаютаА. Таким образом, множества состоят из элементов и в зависимости от их числа бываютконечнымиибесконечными, пустыми (). Для записи множеств используют фигурные скобки, в которых через запятую перечисляются все элементы. Но если множество бесконечное, то перечислить все его элементы мы не сможем. В таких случаях мы будем использовать такую запись:

А= {x| свойство, которым обладают все элементы}.

В нашем курсе мы будем изучать в основном числовые множества.

Далее будем использовать следующие кванторы

• общности вместо слов «для любых» или «для всех (каждого)»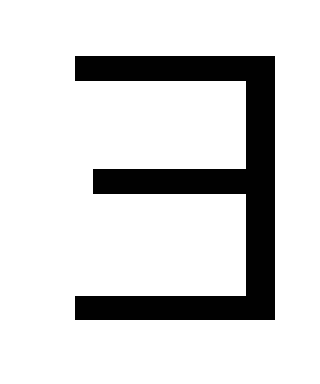

• существования вместо слов «существует» или «есть»

и общепринятые математические символы вместо слов:

• АВ «еслиА,тоВ» или «изАследуетВ»

• АВ «Атогда и только тогда, когдаВ» или «АравносильноВ»

• ˄ знак конъюнкции, заменяет союз «и»

• ˅ знак дизъюнкции, заменяет союз «или»

Множества между собой могут находиться или нет в следующих отношениях:

• пересечения– множества А и В находятся в отношении пересечения (А∩В), если существуют элементы, принадлежащие и одному и другому множествам одновременно и существуют элементы, принадлежащие только множеству А и только множеству В;

• включения– множества А и В находятся в отношении включения, если каждый элемент множества А принадлежит множеству В, говорят, что множество А являетсяподмножествоммножества В и обозначают AB;

• равенства– множестваAиBназываютсяравными (A =B), если они состоят из одних и тех же элементов.

Следствия

1.1. Каждое множество является подмножеством самого себя: AА.

1.2. Пустое множество является подмножеством любого множестваA:  A.

Множества Aиназываютнесобственными подмножествами множестваA, все остальные –собственными подмножествамимножестваA.

Пусть АиВ— некоторые множества.

Определение 1.1.Объединением двух множествАиВназывается множество, состоящееиз тех и только техэлементов, которые принадлежат хотя бы одному из этих множеств. Обозначается: АВ.

На рис. 1 показано объединение множеств А и В при помощи диаграммы Эйлера–Венна.

Рис. 1

Прежде, чем рассмотреть примеры объединения множеств, заметим, что согласно определению объединения хАВхА˅хВ.

Свойства объединения множеств

Из определения следует, что в АÈАвходят те же самые элементы, т.е.АÈА = А. Вообще, когдаBÌA, тоАÈВ = А. В частности,АÈ = А.

Операция объединения подчиняется переместительному закону:

АÈВ = В È А.

Операцию объединения можно распространить на любое число множеств. Когда А,В,С— три произвольные множества, то (АÈВ) È Сесть множество элементов, каждый из которых принадлежит хотя бы одному из множествА,В,С.

В общем случае объединение совокупности множеств обозначается и состоит из элементов, принадлежащих хотя бы одному из множеств .

Операция объединения подчиняется сочетательному закону:

(АÈВ) È С=АÈ(В È С).

Определение 1.2.Пересечением множеств A и B называется множество, состоящее их тех и только тех элементов, которые одновременно принадлежат множествам A и B. Обозначается: АВ.

Согласно определению пересечения хАВхА˄хВ.

Пересечение множеств АиВиллюстрируется на рис. 2.

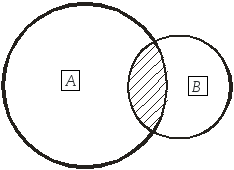
Рис. 2

Свойства пересечения множеств

Очевидно, что АÇА=А; вообще, когдаВА, тоВА=В. Из определения пересечения следует:АВ=ВА, т.е. операция пересечения коммутативна.

Имеет место и следующее равенство: А=.

Операцию пересечения легко распространить и на случай больше двух множеств. Рассмотри три множества А,В,С. ПересечениеАÇВесть множество общих элементов множествАиВ, поэтому (АÇВ)Сесть множество элементов, принадлежащих одновременно трём множествамА,В,С.

Аналогично определяется и операция пересечения любого числа множеств. Из приведенного правила пересечения трех множеств следует, что операция пересечения ассоциативна: (АÇВ)С =А(В ÇС). Поэтому используется записьАÇВС. В общем случае пересечение совокупности множеств (i= 1, 2, …,n) обозначается и состоит из элементов, принадлежащих сразу всем множествам ,.

Заметим, что относительно двух операций пересечения и объединения множеств выполняются два дистрибутивных (распределительных) закона:

1) (А Ç В)  С = (А  С)  (В  С);

2) (А  В)  С = (А  С)  (В  С).

Докажем второй из этих законов (первый доказывается аналогично).

Пусть х Î(АВ)С. Значит,х ÎАВих ÎС. Из того, чтох ÎАВ, следует, что обязательно выполняется по крайней мере одно из двух утверждений:х ÎАилих ÎВ. Когдах ÎА, то из того, чтох ÎС, следует, чтох ÎАС. Значит,х Î(АС)(В С). Когда жех ÎВ, то из того, чтох ÎС, следует, чтох ÎВ С, но тогдах Î(АÇС)(В ÇС).

Таким образом, любой элемент множества (АВ)ÇСявляется элементом и множества (АÇС)È(В ÇС).

Докажем теперь обратное. Пусть х Î(АÇС)È(В ÇС). Возможен один из случаев:х ÎАÇСилих ÎВÇС, т.е.х ÎАих ÎС, илих ÎВих ÎС. Отсюда получаем, чтох ÎСих ÎА  В, а это свидетельствует о том, чтох Î(АÈВ) ÇС. Таким образом, второй дистрибутивный закон доказан полностью.

Определение 1.3.Разностью двух множествAиBназывается множество, состоящееиз тех и только техэлементов множества A, которые не принадлежатВ. Обозначается: А \ В.

Согласно определению разности х ÎА\ВÛх ÎА ˄х В.

Графическое изображение разности А\ВмножествАиВпоказано на рисунке 3 (заштрихованная область — этоА\В).

Рис. 3

Из определения разности следует, в частности, что А\А=;А\ВВ\А.

Определение 1.4.Если множествоB являетсяподмножествоммножестваA, то разность множествA и Bназывается дополнением множестваBдо множестваA. Обозначается:

А \ В=С_АВ илиили

Графическое изображение дополнения множестваВдо множестваАпоказано на рис. 4.

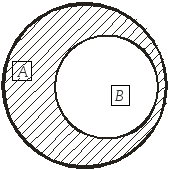
Рис. 4