П.2. Соответствия между множествами. Взаимно однозначные соответствия

Основным объектом математического анализа является «функция». Введем это понятие через понятие «соответствие».

Пусть заданы два множества X и Y. Если для каждого элемента а  Х указан (один, или несколько, или ни одного) элемент b  Y, с которым сопоставляется а, то говорят, что между множествами X и Y установлено соответствие (бинарное отношение).

В основе понятия «соответствия» лежит «упорядоченная пара» (короче «пара»).

Определение 1.5.Упорядоченной паройназывается множество, состоящее из двух элементов, для которых указан порядок следования. Обозначают (х;у); элементхназываютпервой компонентой(координатой),у–второй компонентой(координатой) пары.

Основное свойство пары: две пары равныравны соответственно их компоненты, т.е. (х₁; у₁)=( х₂; у₂) х₁= х₂, у₁ =у₂.

Не следует путать множество {х;у} и пару (х;у): (х;у)(у;х), а {х;у}={у;х}.

Определение 1.6.Упорядоченной тройкой (тройкой)называется пара ((х;у),z), первая координата которой – пара (х;у), а вторая –z. Обозначают (х;у; z).

Аналогично определяются упорядоченные четвёрки, пятёрка, и т. д. n-ки.

Определение 1.7.Декартовым (прямым) произведением множествХиYназывается множество, состоящее из всех возможных пар (х;у), где,и обозначают.

Cпомощью символов это определение можно записать так:

= {(х;у)|,}

Пример 1.1.

Пусть Х= {1, 2, 3},Y= {k,l}. НайтиХ´YиYХ.

Решение. Декартовое произведениеХ´Yсостоит из шести элементов:

ХY = (1,k), (2,k), (3,k), (1,l), (2,l), (3,l).

Выпишем теперь декартовое произведение

YХ = (k, 1), (k, 2), (k, 3), (l, 1), (l, 2), (l, 3).

Таким образом, Х ´ Y  Y  Х (не выполняется ассоциативный закон). Результат декартового произведения зависит от порядка сомножителей.

Принято считать, что для любого множества Хсправедливы равенства:

• ;

• .

Множество называется декартовым квадратом.

Если множества XиY – числовые, то пары элементов (x; y) можно рассматривать как координаты точек на плоскости. В этом случае декартово произведение можно изобразить в декартовой системе координат.

Определение 1.8.Любое подмножество декартового произведения множествназываетсясоответствием между множествамиХиYилиотношением (бинарным отношением) между элементами множеств ХиY.

Будем обозначать соответствия маленькими буквами латинского (f, g,..) и греческого (φ, ψ…) алфавитов. Множество всех первых компонент пар из соответствияfназываютобластью определениясоответствияf(обозначаютD(f)), а множество всех вторых компонент пар из соответствияfназываютобластью значениясоответствияf (обозначаютE(f)).

Пусть f –соответствие между множествамиХиY. Если, то говорят, что «при соответствииf элементxсоответствует элементуy». В этом случае элементуназываетсяобразомэлементах, а элементx–прообразомэлементаy при соответствииf.

Пример 1.2. Между элементами множествX= {2, 3, 5, 11} иY = {6, 7, 9, 10} задано соответствиеf : «числоxявляется делителем числаy».

Очевидно, что f– множество пар элементов(f ={(2, 6), (2, 10), (3, 6), (3, 9), (5, 10)}), находящихся в заданном отношении, является подмножеством декартова произведения множеств

XY= {(2, 6), (2, 7), (2, 9), (2, 10), (3, 6), (3, 7), (3, 9), (3, 10), (5, 6),  (5, 7),  (5, 9), (5, 10), (11, 6), (11, 7), (11, 9), (11, 10)}.

Полным образомэлементаaиз множестваXназывается множество всех элементов изY, которые соответствуют элементуа. Обозначаютf(а). В частности, для примера 1.2

f(2)={6, 10},f(3)={6, 9},f(5)={10},f(11)= .

Полным прообразомэлементаbиз множестваYназывается множество всех элементов из Х, которымbсоответствует. Обозначаютf ^–1(b). В частности, для примера 1.2

f ^–1(6)={2, 3},f ^–1(7)=,f ^–1(9)={3},f ^–1(10)= {2, 5} .

Множество всех элементов из X, имеющих непустые образы, называетсямножеством (областью) определения соответствия, и обозначаютD(f), а множество всех элементов изY, имеющих непустые прообразы –множеством (областью) значений соответствияи обозначаютЕ(f). Так, в примере 1.2 область определения соответствияfесть множествоD(f)={2, 3, 5}, а множество значений соответствияfесть множествоЕ(f)= {6, 9, 10}.

Если множества XиYсовпадают, то говорят об отношении между элементами множестваX.

Замечание 1.1.Соответствие между множествами можно задавать

а) перечислением пар

Y X	6	7	9	10
2				
3			
5				
11

б) таблицей

в) графами

г) с помощью графика (если множества числовые)

Соответствия могут быть различных видов. Приступим к их изучению.

Пусть fсоответствие между элементами множествXиY. Соответствиеfназываетсявсюду определенным, если множествоD(f) = Х. ЕслиE(f) = Y. Если жеE(f)=Y, то соответствие называютсюръективным. На рис. 5аи 5бпредставлено всюду определенное сюръективное соответствие. Соответствия, представленные на рис. 5ви 5г, не сюръективны, а соответствие, изображенное на рис. 5г, не всюду определенное.

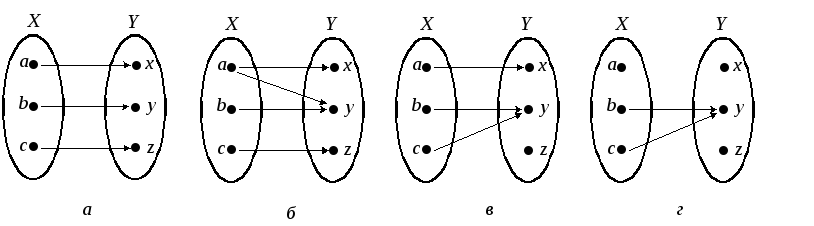
Рис. 5

Соответствие называется инъективным, если любой элемент изE(f) соответствует единственному элементу изD(f). На рис. 5аизображено инъективное соответствие.

Особое место занимают функциональные соответствия.

Определение 1.9. Соответствиеf между множествамиХиY, при котором каждомусоответствует один и только одинназываетсяфункциональным(функцией). Элементназываетсяаргументом функцииf, а соответствующий ему элементназываетсязначением функцииf в точкех.

Определение 1.10. Если область определения функцииf состоит из некоторого множества действительных чисел, тоfназываетсяфункцией одной действительной переменной. Если область определения функцииf состоит из упорядоченныхn-ок действительных чисел, тоfназываетсяфункцией n действительных переменных. Если область значений функцииf состоит из некоторого множества действительных чисел, тоfназываетсядействительной функцией.

Пример 1.3. Среди соответствий, изображенных на рис. 6, функциями будутfиp. Их областями определения будут, соответственно,D(f) = {a, b, c},D(p) = {a, b, c}, а множествами значенийE(f) = {1, 3},E(p) = {1, 2, 3}.

Если _, иf– функциональное соответствие между элементамиxиy, то это записывают так:y = f(x) или или

Рис. 6

Определение 1.7. Соответствие между элементами множествХиY, при котором каждому элементу множестваХ соответствует единственный элемент множестваY, и каждый элемент множестваYсоответствует только одному элементу из множестваХ, называетсявзаимно однозначным (илибиективным).

Определение 1.8.МножестваХиYназываютсяэквивалентными, илиравномощными, если между ними каким-либо способом можно установить взаимно однозначное соответствие.

Эквивалентность двух множеств обозначается так: XY.

Пусть задано соответствие f между множествамиXиY.Обратнымему называется соответствиеf ^–1между множествамиYиX, состоящее из таких пар (у;х), для которых верно, что (х;у)f. Соответствияfиf ^–1называютвзаимно обратными.