
Lab_OE_p1
.pdf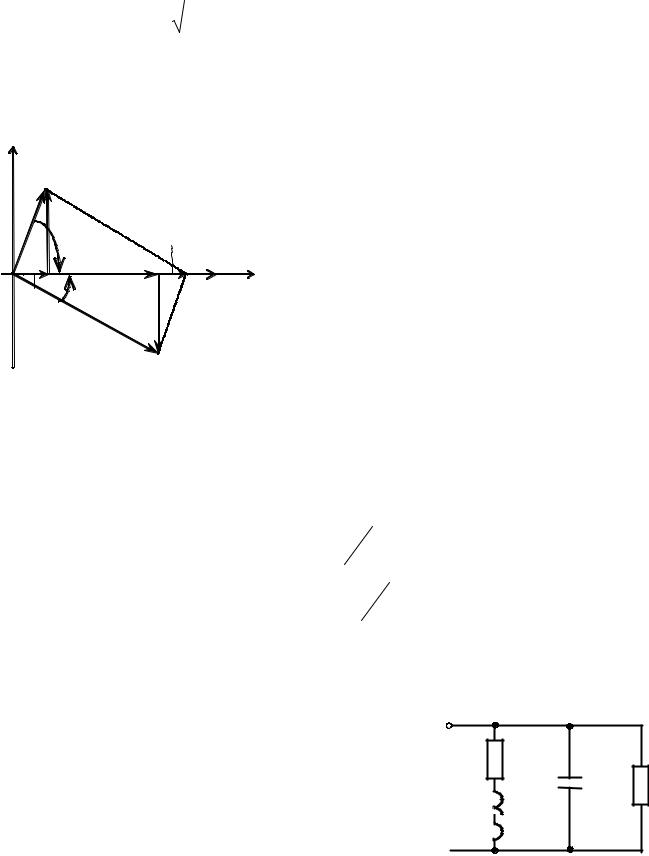
напряжением. Это возможно при условии B=BL-BC=0. Полная проводимость цепи при этом
Y = |
|
|
|
|
|
|
|
|
(G +G |
)2 +(B |
L |
− B )2 |
= G +G |
2 |
= G |
(5.15) |
|
1 2 |
|
C |
1 |
|
|
|||
оказывается минимальной, равной активной проводимости цепи. Ток в неразветвленной части цепи I=GU тоже минимальный, что позволяет обнаруживать резонанс токов по показаниям приборов.
Векторная |
диаграмма токов и напряжения при резонансе |
|
токов |
||||||||||||||||
+j |
|
|
|
строится |
|
так |
же, |
как |
и |
для |
|
любой |
|||||||
|
|
|
параллельной схемы, но с учетом |
||||||||||||||||
I&2 |
|
|
|
||||||||||||||||
|
|
|
|
особенностей |
режима |
(ϕ |
=0, |
I1L=I2C, |
|||||||||||
I&1С |
|
& |
& |
I& = I& |
= I& |
|
+ I& |
) (рис. 5.4). |
|
|
|
|
|
|
|||||
φ2 |
|
I |
= IR |
R |
X |
1R |
|
2R |
X |
|
R , |
то |
I |
|
I |
|
, |
||
|
|
& |
Если |
L |
R |
и |
C |
|
1R |
||||||||||
|
|
|
U |
|
|
|
1 |
|
|
|
2 |
|
1L |
|
|
||||
I&2R φ1 |
I&1R |
I&2L |
|
+1 I2C I2R и I1 I , |
I2 I , т.е. токи в ветвях |
||||||||||||||
|
|
|
значительно больше, чем ток в |
||||||||||||||||
|
I& |
|
|
неразветвленной |
части |
цепи. |
|
Это |
|||||||||||
|
1 |
|
|
свойство - усиление тока - является |
|||||||||||||||
|
|
|
|
||||||||||||||||
|
Рис. 5.4. |
важнейшей |
|
особенностью |
резонанса |
||||||||||||||
токов и широко используется на практике. Оно характеризуется
добротностью контура
|
|
Q = |
I L |
= |
IC |
. |
|
(5.16) |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
I |
I |
|
|
|||
Из условия B=BL-BC =0 можно определить резонансную частоту |
|||||||||||
|
2πf0 L |
− |
|
|
12πf0C |
= 0, |
(5.17) |
||||
|
R12 + (2πf0 L)2 |
R |
2 |
|
|
2 |
|||||
|
|
|
|
+ 1 |
|
|
|
|
|||
|
|
|
2 |
|
2πf0C |
|
|
||||
а также сделать вывод, что резонанса токов можно достичь не только изменением параметров L, C и f, но и R1 и R2.
3. Расчетная часть
3.1 Типовые задачи
Задача 3.1.1. Определить полную комплексную проводимость цепи (рис. 5.5), параметры элементов указаны на схеме в 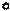
[Ом].
R1=6 XС=5
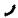 XL=8 R2=10
XL=8 R2=10
Рис. 5.5
Задача 3.1.2. Определить показания амперметров (рис. 5.6), если U=220 В, параметры элементов указаны на схеме в [Ом]. Построить векторную диаграмму токов и напряжения.
&
U
XС=4 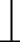 XL=100
XL=100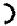 R=50
R=50 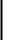

pA1 |
pA2 |
pA3 |
A |
A |
A |
|
Рис. 5.6
Задача 3.1.3. |
Определить |
||
потребляемый |
ток |
I& |
и |
напряжение |
& |
если |
|
U ab , |
|||
известны |
параметры |
||
элементов цепи (рис. 5.7) |
в |
||
[Ом] и входное напряжение
Uвх=12 В. Построить векторную диаграмму токов
и напряжений.
|
I& |
|
R2= 20 3 |
|
XL=10 |
& |
|
& |
a |
U ab |
b |
Uвх |
|
||
|
R1=10Ö3 |
|
XС=20 |
Рис. 5.7
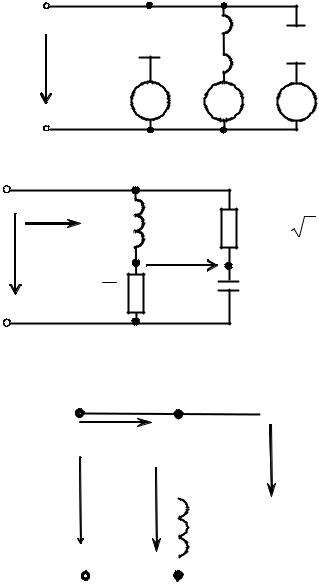
Задача |
3.1.4. |
Однофазный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
I& |
|
|
|
Rд |
|
|
|
|
I&C |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
асинхронный |
двигатель |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
параметрами Rд=30 Ом и Xд = 40 Ом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
включен |
в |
сеть |
переменного |
U |
|
|
|
|
I&дв |
C |
|
|
|
|
|||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||
напряжения 220 В. |
|
|
|
|
|
|
|
|
|
|
|
Xд |
|
|
|
|
|
||
Какой |
|
величины |
нужно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
подключить |
емкость |
С, |
чтобы |
|
|
|
|
|
Рис. 5.8. |
|
|
|
|
|
|||||
коэффициент |
мощности цепи |
стал |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
равен 0,9? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3.1.5. К асинхронному двигателю, полезная мощность |
|||||||||||||||||||
которого P=3,7 кВт, |
КПД η |
=83,5 |
%, |
|
сопротивления проводов |
||||||||||||||
Rпр=2 Ом, |
подается напряжение |
U=380 |
В. Двигатель |
работает с |
|||||||||||||||
cosϕдв=0,707. Какую емкость нужно включить параллельно двигателю, чтобы повысить cosϕ до 0,9? Как изменяются при этом потери мощности и напряжения в линии?
3.2. Задачи для самостоятельного решения
Задача 3.2.1. Катушка (Rк и XL) и конденсатор (XC) соединены параллельно, причем контур настроен в резонанс. Ток в конденсаторе 10А, суммарный ток 5 А. Определить ток в катушке.
Задача 3.2.2. Определить значение емкостной составляющей тока I&, если известны параметры элементов цепи в [Ом] и U=100 В (рис.
5.9).
|
I& |
R2=80 |
|
|
& |
XL=40 |
XС3=100 |
||
|
||||
U |
|
|
|
|
|
R1=30 |
|
XС2=60 |
|
|
|
|
Рис. 5.9.
+j
Задача |
3.2.3. |
По |
векторной |
|
I&3 |
|
|
|
|
|
|
|
|||||
диаграмме |
|
|
(рис. 5.10) |
|
60° |
I& |
& |
|
|
|
|
|
|
|
|||
восстановить |
|
электрическую |
|
|
1 |
U +1 |
||
|
|
|
-300 |
I& |
||||
схему |
и ее |
параметры, если |
|
|
||||
|
|
|
|
|
|
|
|
|
известно, что U=50 В, I1=5 А, |
|
|
|
|
||||
I2=10 А, I3=2,5 А. |
|
|
|
|
|
|||
Задача |
3.2.4. |
Определить |
|
|
I&2 |
|
||
|
|
Рис. 5.10. |
|
|||||
показания приборов pA, pV |
|
* |
|
|||||
и pW (рис. |
5.11), если до |
* |
pA |
|
||||
|
|
|||||||
W |
A |
|
||||||
включения |
выключателя |
|
|
|||||
|
pW |
|
|
|||||
SA1 коэффициент мощности |
|
R |
|
|||||
|
|
|
||||||
цепи был cosϕ1=0,6, а после |
|
|
pV V |
SA1 |
||||
его включения |
стал |
cosϕ |
|
|
|
|||
=0,92. |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
L |
C |
|
Емкость конденсатора, |
|
|
|
|
||||
необходимая |
|
|
для |
|
|
I& |
|
|
улучшения |
коэффициента |
|
|
|
||||
|
|
Рис 5.11. |
|
|||||
мощности |
в |
указанных |
|
|
|
|||
& |
|
|
|
|||||
пределах, |
C=200 |
мкФ, |
U |
|
|
|
||
реактивная |
|
|
мощность |
|
|
I&1 |
I&2 |
|
конденсатора QC =3,2 квар. |
|
|
||||||
|
|
|
|
|
|
|
Д1 |
Д2 |
Рис. 5.12.
Задача 3.2.5. В электрическую цепь (рис. 5.12) включены два электродвигателя Д1 и Д2. Определить ток I в цепи и общий коэффициент мощности сosϕ.
Какую емкость нужно включить параллельно, чтобы повысить сosϕ1 до сosϕ2=0,94? Двигатели имеют следующие номинальные данные:
P1н=60 Вт; U1н=220 В; η1=0,8; сosϕ1=0,65; P2н=90 Вт; U2н=220 В; η2=0,75; сosϕ2=0,77.
4. Экспериментальная часть
4.1. Описание установки
Экспериментальные исследования проводятся на универсальном лабораторном стенде.
При сборке цепи используется следующее оборудование : -лабораторный автотрансформатор (ЛАТР);
-индуктивная катушка;
-блок конденсаторов от 1 до 30 мкФ; -электроизмерительные приборы :
а) pA1, pA2, pA3 - амперметры с пределами измерений 0,25÷1 А;
б) pV - вольтметр с пределом измерения 150 В, встроенный в стенд, регистрирующий величину входного напряжения, регулируемого автотрансформатором (АТ);
в) pW - ваттметр с пределами измерений 1 А и 150 В; г) pϕ - электронный фазометр.
Схема эксперимента представлена на рис. 5.13.
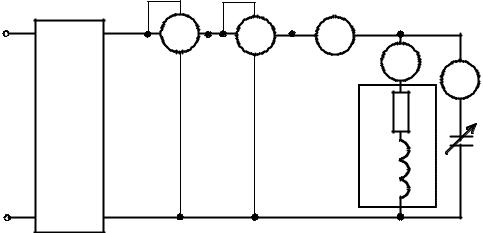
U* |
pW |
U* |
pϕ |
|
|
|
|
|
|
|
pA1 |
|
|
||
* |
|
* |
ϕ |
|
|
|
|
W |
|
A |
pA2 |
|
|||
I* |
I |
I* |
|
I |
A |
pA3 |
|
|
|
|
|
|
A |
||
|
|
|
|
|
|
A |
|
ЛАТР |
|
|
|
|
RK |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LK |
|
|
U |
|
U |
|
|
|
|
|
|
Рис 5.13 |
|
|
|
|
||
4.2. Методические указания к выполнению работы
4.2.1.Записать технические данные используемых приборов в отчет.
4.2.2.Собрать электрическую цепь (рис. 5.13).
4.2.3.Установить с помощью автотрансформатора (АТ) напряжение
на входе цепи (70÷90) В по указанию преподавателя.
4.2.4. Произвести измерения I, Iк, IС, P, ϕ в цепи при различных величинах емкости конденсатора C: три-четыре замера до резонанса, при Срез и три-четыре замера после резонанса. Резонанс определить из условия ϕ =0; I→min.
Результаты эксперимента занести в табл. 5.1.
Таблица 5.1.
|
|
Измерено |
|
|
|
|
|
Вычислено |
|
|
||||
№ |
С, |
U, |
I, |
Iк, |
IC, |
P, |
ϕ, |
Zк, |
Rк, |
XL, |
BL, |
G, |
BC, |
Y, |
мкФ |
В |
А |
А |
А |
Вт |
град |
Ом |
Ом |
Ом |
См |
См |
См |
См |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3. Рабочее задание
4.3.1.Выполнить необходимые расчеты для таблицы 5.1.
4.3.2.Построить графики зависимостей: I=f(C); Iк=f(C); IC=f(C);
ϕ=f(C); I=f(C).
4.3.3. Построить три векторные диаграммы токов и напряжения для случаев : C<Cрез; C=Cрез; C>Cрез. (в масштабе).
5. Контрольные вопросы
5.1.Как определяются активная, индуктивная и емкостная проводимости исследуемой цепи?
5.2.Что называется активной и реактивной составляющими тока?
5.3.Какое соотношение определяет сдвиг по фазе между током и напряжением в цепи при параллельном соединении RL и RC- ветвей.
5.4.С помощью каких приборов и по каким признакам можно судить о возникновении резонанса токов в цепи?
5.5.Почему резонанс токов широко используется для компенсации
коэффициента мощности (сosϕ) промышленных установок?
Лабораторно-практическое занятие № 6
ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПРИ СОЕДИНЕНИИ НАГРУЗКИ ЗВЕЗДОЙ
1. Цель занятия
Исследование трехфазной электрической цепи при различных режимах работы приемников, соединенных звездой. Приобретение навыков построения топографических диаграмм напряжений и векторных диаграмм токов.
2. Краткие теоретические сведения
Под трехфазной системой понимается совокупность электрических цепей, в которых действуют синусоидальные ЭДС (напряжения) одной и той же частоты, сдвинутые относительно друг друга по фазе на угол 2π/3 (120°) и создаваемые общим источником электрической энергии.
Передача электрической энергии от источника к потребителю в трехфазной трехпроводной системе осуществляется с помощью линейных приводов. В четырехпроводной системе имеется четвертый - нейтральный (N – n) - провод, соединяющий общие точки фаз источника и потребителя.
Соединение, при котором концы всех трех фаз потребителя объединяются в общую точку, называемую нейтральной или нулевой, а начала фаз присоединяются к трехфазному источнику питания посредством линейных проводов, называется соединением звездой.
На практике применяются две схемы соединения звездой трехфазного потребителя:
1- звезда с нейтральным (нулевым) проводом (рис. 6.1); 2- звезда без нейтрального (нулевого) провода (рис. 6.2).
Токи I&A ,I&B ,I&C в соответствующих линейных проводах называются линейными; токи, протекающие по фазам – фазными, а ток I&n в нейтральном проводе называется нейтральным. Напряжения
& |
& |
& |
|
между линейными проводами потребителя U AB ,U BC ,UCA называются |
|||
|
|
& & & |
- |
линейными, а между началом и концом фаз потребителя U a ,Ub ,Uc |
|||
фазными.
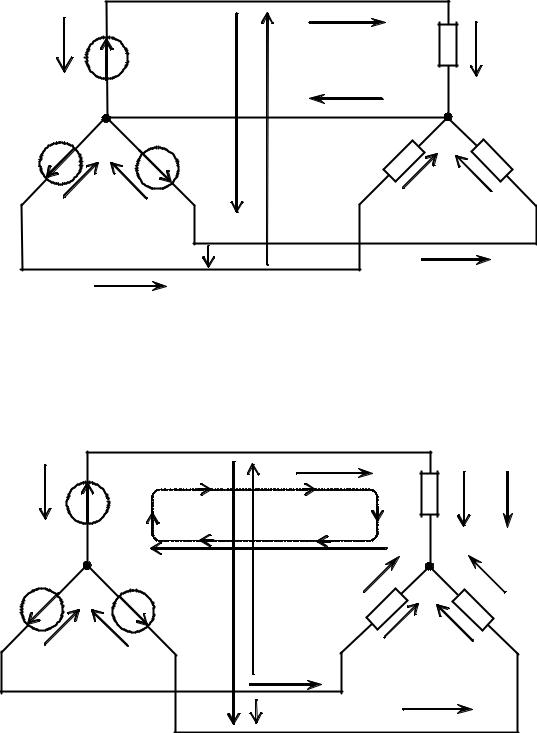
A |
a |
|
& |
& |
|
I& |
Z a |
|
& |
|
U A |
EA |
& |
A |
|
Ua |
|
|
|
|
U AB |
& |
|
|
|
|
|
|
|
In |
|
|
|
|
N |
|
|
|
|
n |
|
|
& |
|
|
|
|
|
|
|
EC |
|
& |
|
Z c |
|
Z b |
|
|
|
EB |
& |
|
||
|
|
|
|
UCA |
|
|
|
C |
|
|
B |
c |
& |
& |
b |
& |
& |
Uc |
Ub |
||||
|
UC |
U B |
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
U BC |
|
|
|
|
|
|
|
I&C |
|
|
|
I&B |
|
|
|
|
Рис. 6.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
a |
|
|
|
|
& |
|
|
|
I&A |
|
|
|
|
& |
|
|
& |
|
|
|
|
& |
|
||
|
U |
|
|
|
|
Z a |
|
Ia |
||
|
|
A |
EA |
|
& |
|
Ua |
|
||
|
|
|
|
|
U nN |
|
|
|
|
|
|
& |
N |
|
|
|
I& |
n |
I&b |
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
EC |
|
|
& |
|
|
|
|
|
|
|
|
|
|
EB |
& |
Z |
|
|
Z |
|
|
|
|
|
& |
|
|
|
|||
|
|
|
|
UCA |
c |
|
b |
|||
|
|
|
|
U AB |
|
|
|
|||
C |
|
|
|
B |
c |
|
& |
& |
|
b |
|
& |
& |
|
Uc |
Ub |
|
||||
|
|
UC |
U B |
|
I&C |
|
|
I&B |
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U BC |
|
|
|
|
|
Рис. 6.2
При соединении потребителя звездой фазные токи Iф равны соответствующим линейным: Iф = Iл. Между линейными и фазными

напряжениями потребителя |
существуют |
следующие |
соотношения, |
|
(согласно второму закону Кирхгофа): |
|
|
|
|
& |
& |
& |
|
|
U AB =U a |
−Ub ; |
|
||
& |
& |
& |
; |
(6.1) |
U BC = Ub |
−Uc |
|||
& |
& |
& |
|
|
UCA = Uc −U a . |
|
|||
Между фазными Uф и линейными Uл напряжениями существует соотношение (в случае симметричного соединения нагрузки звездой)
U л = |
|
Uф. |
(6.2) |
3 |
Фазные токи потребителя определяются по закону Ома:
&
I&a = Ua ; Z a
&
I&b = Ub ; (6.3)
Z b
&
I&c = Uc . Z c
Нагрузка, при которой комплексные сопротивления всех фаз потребителя равны между собой ( Z a = Z b = Z c ), называется
симметричной. При симметричной нагрузке для цепи без нейтрального провода и для цепи с нейтральным проводом токи в фазах будут равны:
|
|
|
+1 |
|
|
|
|
|
A (a) |
|
|
& |
& |
|
|
|
|
Ua =U A |
|
|
|
|
|
|
& |
|
& |
|
|
|
|
U |
AB |
|
|
+j |
UСA |
I&c |
|
|
|
|
N (n) & |
& |
|||
|
|
|
|
Ub |
=U B |
|
|
|
I&b |
|
|
C (c) |
& & |
& |
|
B (b) |
|
|
Uc =UC |
U BС |
|
|
|
Рис. 6.4
|
I&a |
|
= |
|
I&b |
|
= |
|
I&c |
|
, |
(6.4) |
|
|
|
|
|
|
|||||||
I&a + I&b + I&c = 0. |
(6.5) |
|||||||||||
При этом, например, для схемы на рис. 6.3, векторная диаграмма токов и напряжений имеет вид, представленный на рис. 6.4.
Iф = |
Uф |
. |
(6.6) |
|
|||
|
Zф |
|
|
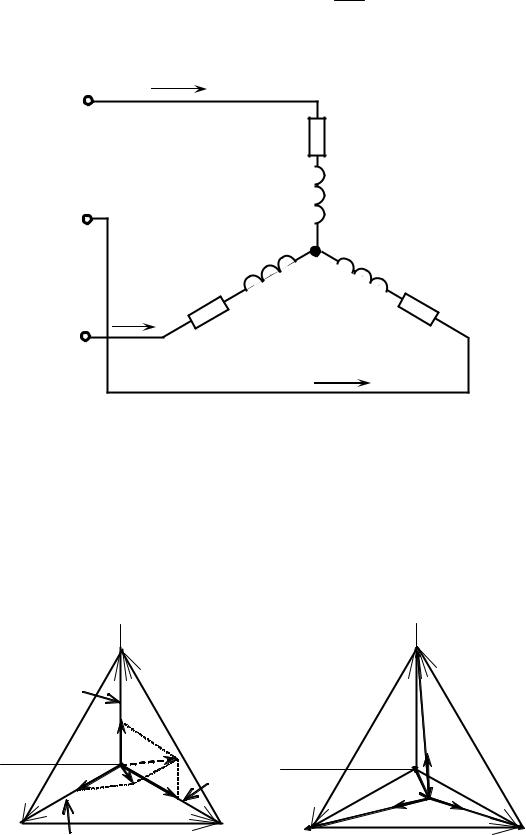
|
tgja = tgjв = tgjc |
= X ф , |
(6.7) |
|
|
|
Rф |
|
|
|
I& |
a |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
Rф |
|
|
|
|
XLф |
|
|
B |
|
|
|
|
|
XLф |
n |
XLф |
|
|
|
|
||
|
Rф |
|
|
Rф |
|
I&C |
|
|
|
C |
c |
|
|
b |
|
I&B |
|
|
|
|
|
|
|
|
|
Рис. 6.3 |
|
|
|
При несимметричной нагрузке и наличии нейтрального провода: |
||||
|
I&a ¹ I&b ¹ I&c , |
|
|
(6.8) |
|
I&0 = I&a + I&b + I&c |
|
(6.9) |
|
При этом векторная диаграмма токов и напряжений для |
||||
несимметричной активной нагрузки с нейтральным проводом имеет |
||||
вид, представленный на рис. 6.5. |
|
|
|
|
|
|
|
|
A (a) |
+1 |
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A (a) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
& |
|
& |
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
U |
A |
= U |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U AB |
|
|
& |
|
|
|
|
|
& |
|
||
|
|
|
|
|
|
|
|
|
|
& |
|
& |
|
|
||
|
|
|
|
|
& |
|
|
|
U |
СA |
|
|
U |
AB |
||
|
|
|
|
|
|
|
|
|
U A |
|
Ua |
|
|
|||
|
|
& |
|
|
Ia |
|
|
|
|
|
|
|
|
|
|
|
+j |
UСA |
N (n) |
|
|
|
|
+j |
|
N |
|
I&a |
|
|
|
||
|
|
|
I&c |
|
I&b |
& |
|
& |
& |
& |
|
n |
I& |
& |
|
|
|
|
|
|
& |
|
|
UB |
= Ub |
UC |
UnN |
b |
UB |
||||
|
|
|
|
In |
|
|
|
|
|
|
& |
I& |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uc |
C Ub |
|
|
||
C (c) |
|
& |
& |
& |
|
|
|
|
|
& |
|
|
|
|
|
|
|
U |
BС |
B (b) |
C (c) |
|
|
|
|
|
B (b) |
||||||
|
|
|
UC |
= Uc |
|
|
UBС |
|
|
|||||||
|
|
|
|
Рис. 6.5 |
|
|
|
|
|
Рис. 6.6 |
|
|
|
|||
