
Lab_1_2
.pdf1 ЛАБОРАТОРНАЯ РАБОТА № 1. ИЗУЧЕНИЕ СПОСОБОВ ПРЕДСТАВЛЕНИЯ ДАННЫХ В ЭВМ
1.1 Цель и задачи лабораторной работы
Цель: изучение способов представления числовых, текстовых данных, основных
арифметических и логических операций над ними.
Задачи:
исследование представления в ЭВМ целых чисел;
исследование представления в ЭВМ вещественных чисел с плавающей запятой;
анализ стандарта IEEE 754 для организации хранения вещественных чисел
сплавающей запятой;
исследование особенностей операций над числами с плавающей запятой;
анализ представления текстовых данных
1.2Краткие теоретические сведения
1.2.1 Порядок байт при хранении многобайтного представления числа
M может быть использовано многобайтное в этом случае будет представлено в виде ряда в
MAi·256i A0·2560 A1·2561 A2·2562 An·256n
i0
Коэффициенты представляют собой последовательность байтов,
образующих исходное число M . Коэффициент A0 называется младшим байтом, а An –
старшим байтом числа M.
По порядку записи байтов многозначного числа выделяют следующие варианты:
1. Порядок от старшего к младшему (big-endian)
Запись многобайтного числа начинается со старшего и заканчивается младшим байтом:
An, , A0
Порядок используется:
в стеке протокола TCP/IP (сетевым порядком байтов); 1
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |
в процессорах IBM, Motorola, SPARC.
во многих форматах файлов (PNG).
2.Порядок от младшего к старшему (little-endian)
Запись многобайтного числа начинается с младшего и заканчивается старшим байтом:
A0, , An
Порядок используется:
при организации памяти x86-процессоров;
в протоколах и форматах USB, конфигурациях PCI.
Преимущества:
возможность «неявной типизации» целых чисел при чтении меньшего объёма байт.
int32: |
0x0000002216 = 3410 |
int16: |
0x002216 = 3410 |
int8: |
0x2216 = 3410 |
3. Переключаемый порядок
Многие процессоры могут работать и в порядке от младшего к старшему, и в обратном, например, ARM, PowerPC.
4. Смешанный порядок
Иногда используется при работе с числами, длина которых превышает машинное слово (представление 4-байтных целых чисел на 16-битных процессорах семейства PDP-11).
Доступ к 4-байтному числу в оперативной памяти может производиться как к 32-
разрядному слову, так и побайтно.
Если исходное число представлено в шестнадцатеричной записи, то: 0xA1B2C3D416 = D4*0x01 + C3*0x100 + B2*0x10000 + A1*0x1000000
Порядок от младшего к старшему |
0xD4, 0xC3, 0xB2, 0xA1 |
Порядок от старшего к младшему |
0xA1, 0xB2, 0xC3, 0xD4 |
Размещение байтов слова в памяти Big-endian и Little-endian ЭВМ |
|
|
2 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |

Хранение вещественных чисел с плавающей запятой при использовании используются формата IEEE 754 со знаком и порядком числа в старших байтах также зависит от порядка байт.
В языке С/С++ возможно использование переменных, содержащих в разные моменты времени объекты различных типов и размеров. Данный механизм обеспечивается использованием объединений (union). Фактически, объединение представляет собой структуру, все элементы которой имеют нулевое смещение относительно ее начального адреса. Размер структуры позволяет разместить в ней самый большой элемент с соответствующим механизмом выравнивания. Для прямого доступа к полям внутри слова может быть использовано битовое поле – набор соседних бит внутри слова.
Объединения позволяют определить порядок байт при хранении многобайтного целого числа. Пример программного кода на языке С/С++, который позволяет осуществить подобную проверку, приведен ниже:
//Представление двухбайтного беззнакового целого в виде числа и массива байт.
//integerValue = 1 = 0x0001
//Если порядок от младшего к старшему (little-endian), то будет:
//[00000001] [00000000] = [0x01] [0x00]
//Елси порядок от старшего к младшему (big-endian), то будет:
//[00000000] [00000001] = [0x00] [0x01]
union ByteOrder {
unsigned char bytesArray[2];
unsigned short integerValue;
};
//Представление двухбайтного беззнакового целого в виде числа и массива байт.
//integerValue = 1 = 0x0001
//Если порядок от младшего к старшему (little-endian), то будет:
//[00000001] [00000000] = [0x01] [0x00]
//Елси порядок от старшего к младшему (big-endian), то будет:
//[00000000] [00000001] = [0x00] [0x01]
union ByteOrder {
unsigned char bytesArray[2]; unsigned short integerValue;
|
3 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |

};
1.2.2 Представление целых чисел без знака
Целое число может быть представлено в виде степенного ряда:
Xq xn 1qn 1 xn 2qn 2 x0q0 x 1q 1 x mq n
где xi — разрядный коэффициент; qi — весовой коэффициент.
Целое число без знака в памяти ЭВМ будет представлено в прямом коде,
следовательно, десятичное число необходимо перевести из десятичной системы счисления в двоичную систему. Например, число 12310 можно представить в виде суперпозиции по степеням двойки:
12310 6410 3210 1610 810 210 110 26 25 24 23 21 20 11110112
1.2.3 Представление целых чисел со знаком
Как правило, для того чтобы задать знак числа используются один или два старших разряда числа. Отрицательные целые числа могут быть представлены в обратном или дополнительном коде.
Для перевода целого числа со знаком из десятичной системы счисления в дополнительный код необходимо:
1.получить двоичное представление модуля числа,
2.найти двоичное дополнение числа до единицы (инвертировать разряды),
3.добавить к результату единицу.
Перевод числа 8410 в дополнительный код, согласно данному алгоритму:
1. |
84 |
84 |
26 24 22 01010100 |
2 |
– перевод q |
p |
2 |
|
10 |
10 |
|
10 |
|
2.010101002 101010112 – инвертирование двоичного представления
3.101010112 12 101011002 – добавление единицы к результату.
Для преобразования целого числа в систему счисления с произвольным целочисленным основанием может быть использована функция библиотеки stdlib.h
языка С/С++:
char *_itoa(
int value, // исходное число
|
4 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |

char *str, |
// |
строковый |
буфер |
для хранения результата |
int radix |
// |
основания |
новой |
системы счисления |
);
1.2.4 Представление вещественных чисел в формате с плавающей запятой
Десятичное число 155,625 в нормализованном экспоненциальном виде:
|
1,55625·10 2 1,55625·102 . |
Число |
1,55625·102 состоит из двух частей: мантиссы M 1,55625 и экспоненты |
e10 2. Если |
мантисса находится в диапазоне 1 M 10, то число считается |
нормализованным. Экспонента представлена основанием системы исчисления – 10 – и
порядком – 2. Порядок экспоненты может иметь отрицательное значение, например число:
0,0155625·10 2 1,55625·10 2
Десятичное число 155,625 в денормализованном экспоненциальном виде:
0,155625·103 0,155625·103
Если мантисса находится в диапазоне 0,1 M 1, то число считается денормализованным.
Для представления всех вещественных чисел кроме нуля используется нормализованная форма, когда нулевой разряд мантиссы M0 равен 1. При таком представлении нулевой разряд опускается, и хранятся только разряды M1 ... Mn. Таким образом, мантисса M удовлетворяет неравенству 1 <= M < 2.
Машинное представление вещественных чисел содержит конечное число элементов. Только некоторые вещественные числа могут быть точно представлены описанным выше способом. Такие вещественные числа называются точно представимыми или просто представимыми в используемой машинной арифметике.
Даже простые на вид рациональные числа, такие как 0.1, оказываются непредставимыми. Непредставимое число заменяется ближайшим представимым числом.
Преобразование десятичного числа в двоичное число с плавающей запятой.
|
5 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |
Необходимо представить десятичное число с плавающей запятой в виде
двоичного числа с плавающей запятой в экспоненциальном нормализованном виде.
Осуществим разложение числа 155,62510 в двоичный степенной ряд:
155,625 1·27 0·26 0·25 1·24 1·23 0·22 1·21 1·20 1·2 1 0·2 2 1·2 3
155,625 128 0 0 16 8 0 2 1 0,5 0 0,125
155,62510 10011011,1012
Полученное число необходимо привести к нормализованному виду:
1,55625·102 1,0011011101·2111
Внимание следует обратить на показатель степени основания системы счисления
– он также представлен в двоичном виде.
Ассоциацией IEEE (Institute of Electrical and Electronics Engineers) разработан стандарт IEEE 754, который используется для представления чисел с плавающей запятой в двоичном коде в архитектуре микропроцессоров x86.
Преобразование двоичного нормализованного числа в 32 битный формат
IEEE 754.
Алгоритм преобразования в 32 битный формат IEEE 754:
1.Отводится 1 самый старший бит в 32 битной последовательности для обозначения знака числа:
0-положительное
1-отрицательное
2.Используется понятие смещенной экспоненты, что позволяет не выделять отдельный бит для хранения знака. Исходный диапазон возможных значений экспоненты сдвигается из диапазона [-127; 128] в диапазон [0; 255] путем прибавления
кзначению экспоненты смещения, равного 127. Для хранения смещенной экспоненты предназначен следующий байт (8 бит). Для определения знака экспоненты добавляют смещение к экспоненте в половину байта +127(0111 1111).
Если экспонента равна 710 = 1112, то смещенная экспонента равна 7 + 127 = 13410.
Если экспонента равна -7 , то смещенная экспонента равна 127 - 7 = 12010.
|
6 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |
При обратном преобразовании смещенной экспоненты в экспоненту двоичного нормализованного числа необходимо вычесть из данного байта значение 127.
3. Последние 23 бита предназначены для хранения мантиссы числа. Так как в нормализованной двоичной записи первый бит мантиссы равен 1, то в 23 бита записывается остаток от мантиссы.
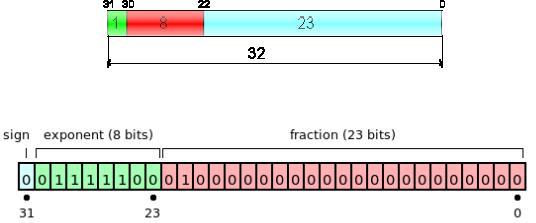
Десятичное число 155,625 в 32-х битном формате IEEE754 представляется следующим образом:
1 бит |
8 бит |
23 бит |
IEEE 754 |
|
02 |
1000 01102 |
001 1011 1010 |
431BA00016 |
|
0000 0000 00002 |
||||
|
|
|
||
010 |
13410 |
181043210 |
|
|
знак числа |
смещенная экспонента |
остаток от мантиссы |
155,62510 IEEE754 |
Преобразования числа формата 32 бит IEEE 754 в десятичное число
Чтобы восстановить число, необходимо иметь три параметра:
S - бит знака (31-й бит)
E - смещенная экспонента (30-23 биты)
M - остаток от мантиссы (22-0 биты)
Каждый параметр представляет собой целое в двоичном виде.
Рисунок 1. Представление вещественного числа в формате с плавающей запятой
Для получения десятичного числа из числа IEEE754 одинарной точности необходимо:
|
7 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |
F 1 |
S |
|
E 127 |
M |
||
|
2 |
1 |
|
|
|
|
|
2 |
23 |
||||
|
|
|
|
|
|
|
где F - десятичное число
Восстановим число 1,55625·102 1,0011011101·2111 :
F ( 1) |
0 |
134 127 |
|
1810432 |
|
7 |
|
|||||||
|
·2 |
· 1 |
|
|
|
|
2 |
|
·(1 0,2158203125) 128·1,2158203125 155,625 |
|||||
|
2 |
23 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
- |
добавляется |
единица нормализованного представления, а остаток |
||||||||||
1 |
|
|
|
|||||||||||
2 |
23 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мантиссы в десятичном виде находим отношением двух целых чисел – остатка мантиссы к целому.
В IEEE754 число «0» представляется значением с порядком, равным E = -127 и
нулевой мантиссой.
Также в IEEE754 предусмотрено представление для специальных чисел, работа с которыми вызывает исключение. К таким числам относится бесконечность (±∞) и
неопределенность (NaN).
Неопределенность или NaN (от not a number) – это представление, придуманное для того чтобы арифметическая операция могла всегда вернуть осмысленное значение.
NaN можно получить: ∞+(- ∞)
0 × ∞ 0/0, ∞/∞
sqrt(x), где x<0
По определению NaN ≠ NaN, поэтому, для проверки значения переменной необходимо сравнить ее саму с собой.
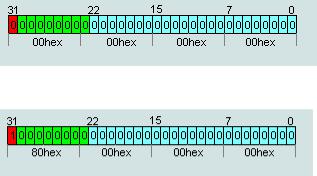
Представление специальных чисел в стандарте IEEE754
1. число IEEE754=00 00 00 00hex считается числом +0
число IEEE754=80 00 00 00hex считается числом -0
|
8 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |

2. число IEEE754=7F 80 00 00hex считается числом +∞
число IEEE754=FF 80 00 00hex считается числом -∞
При сравнении +0=-0. Если бы у нуля не было знака, выражение 1/(1/x)=x не выполнялось бы верно при x=±∞, так как 1/∞ и 1/-∞ равны 0.
Пример:
(+∞/0) + ∞ = +∞, тогда как (+∞/-0) +∞ = NaN
Если в арифметическом выражении появился NaN, результатом всего выражения всегда будет NaN. Если же в выражении встретилась бесконечность, то результатом может быть ноль, бесконечность или обычное число с плавающей запятой. Например, 1/∞=0.
1.2.5 Особенности использования чисел с плавающей запятой
Величина относительной ошибки в языке С/С++ имеет размерность для типа данных float 10-6 , для double 10-14
Величины абсолютных ошибок могут быть достигать для float величины 1031 и
для double 10292:
float a, b, f;
a=123456789;
b=123456788;
f=a-b;
printf("Result: %f\n", f);
Result: 8.000000 (Ответ должен быть 1.000000)
Абсолютная ошибка равна +7.
|
9 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |
123456789 в float = 4CEB79A316 = 12345679210 абсолютная ошибка представления равна +3.
123456788 в float = 4CEB79A216=12345678410 абсолютная ошибка представления равна -4.
Относительная погрешность исходных чисел приблизительно равна 3,24e-6%. В
результате одной операции относительная погрешность результата увеличилась в
2,5e+8 раз.
Во-первых, работать с вещественными числами с плавающей запятой можно только в узком диапазоне числовой оси, где мантиссы пересекаются.
Во-вторых, для каждого исходного вещественного числа с плавающей запятой
существует предел выполнения цикла.
Если существует цикл, в котором исходное число прибавляется к сумме, то существует численный предел суммы для этого числа. То есть, сумма, достигнув определённой величины, перестает увеличиваться от сложения её с исходным числом.
Пусть имеется фармацевтический цех, производящий таблетки весом 10мг.
Состоящий из:
формовочной машины,
накопительного бункера на 500 кг,
фасовочной машины,
автоматической системы управления.
Формовочная машина подает в бункер по 10 таблеток одновременно.
Фасовочная машина забирает по одной таблетке.
Автоматическая система управления учитывает таблетки, поступившие в бункер от формовочной машины и взятые из бункера фасовочной машиной, а также показывает заполнения бункера продукцией в кг. Когда в бункере будет более 500 кг продукции, формовочная машина встает на паузу до тех пор, пока в бункере не станет
200 кг продукции. Фасовочная машина остановится, если в бункере будет менее 10 кг и запустится, когда в бункере будет более 100 кг продукции.
Обе машины могут периодически останавливаться для обслуживания не зависимо друг от другу (благодаря бункеру).
|
10 |
Д.И. Кардаш, А.М. Вульфин |
Лабораторные работы СВТ |
