3.4. Равномерное распределение

Определение. Распределение непрерывной случайной величины, заданное дифференциальной функцией распределения

(6)

называется равномерным распределениемна отрезке.

График функции (6) изображен на рис. 14.2.

Интегральный закон равномерного распределения имеет следующий вид:

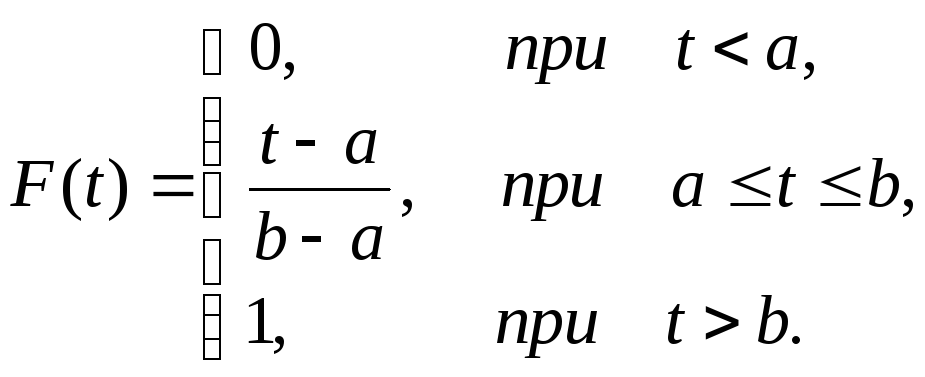(2)

График функции (7) изображен на рис. 14.3.

Найдем, где– равномерно распределенная случайная величина.

Имеют место следующие случаи:

а)(рис. 14.4),

;

б) (рис. 14.5),

;

в) (рис. 14.6),

.

Если ,, то.

Моделью равномерного распределения может служить пример с рулеткой (см. выше).

Теорема. Если– равномерно распределенная непрерывная случайная величина на отрезке, то

,,(8)

3.5 Показательное (экспоненциальное) распределение

Определение.Распределение непрерывной случайной величины, заданное дифференциальной функцией распределения

(9)

где – некоторый параметр, называетсяпоказательным(экспоненциальным) распределением.

График функции (9) изображен на рис. 14.7.

Интегральная функция распределения показательной величиныимеет вид:

(10)

Действительно,

Вычислим показательной случайной величины.

а) :

;

б) :

;

в) :

.

Теорема. Если– показательная случайная величина с дифференциальной функцией распределения (9), то

,,(11)

§ 4. Система случайных величин

Пусть в результате некоторого испытания случайные величины ипринимают значенияи. Эта пара чисел задает точку на плоскости. По аналогии с интегральной функцией распределения одной случайной величины можно рассматривать функцию, равную вероятности.

Функция

(1)

называется интегральной функцией распределения системы двух случайных величини.

Аналогично, интегральная функция совместного распределенияслучайных величинесть по определению функция

. (2)

Как видно из рис. 14.8, функциявыражает вероятность попадания точкив заштрихованную область.

С помощью интегральной функции распределения можно вычислить вероятностьтого, что пара значений величинибудет удовлетворять неравенствами, т.е. принадлежать прямоугольнику (рис. 14.9), а именно

. (3)

Аналогом дифференциальной функции распределения случайной величины для пары случайных величин является функция

. (4)

Можно доказать, что

(5)

с точностью до бесконечно малых более высокого порядка малости, чем ,.

Функция называетсяплотностью вероятности системы величини.

Формула (5) оправдывает такое название функции (есть вероятность, отнесенная к единице площади).

Пусть – область на плоскости переменных,и требуется найти вероятность, т.е. вероятность того, что значения пары случайных величиниопределят координаты некоторой точки из.

Разобьем область на малые прямоугольники со сторонами, параллельными осям координат (рис. 14.10). Тогда искомая вероятность (в соответствии с формулой (5)) будет приближенно равна сумме

,

где,– координаты левой нижней вершины прямоугольника с номером. Предел этой суммы (если он существует) по определению равен двойному интегралу

.

Таким образом, получаем формулу

. (6)

Формула (6) есть двумерный аналог формулы .

Из формулы (6) следует, что

,

поскольку в этом случае двойной интеграл означает вероятность достоверного события .

Замечание.По аналогии с одномерной случайной величиной функциииобладают следующими свойствами:

1. ;

2. – неубывающая по аргументу функция;

3. , т.к.– достоверное событие;

, т.к.– достоверное событие;

4. ;

5. ;

6. .

Рассмотрим теперь совместное распределение двух дискретных случайных величин. Пусть и– значения случайных величини, аи– соответствующие им вероятности; пустьозначает вероятность совместного наступления событий,. Соответствиеназываетсясовместным распределением пары дискретных случайных величин.

Закон совместного распределения двух случайных величин часто изображают с помощью таблицы:

				…
				…
				…
	…				…
				…

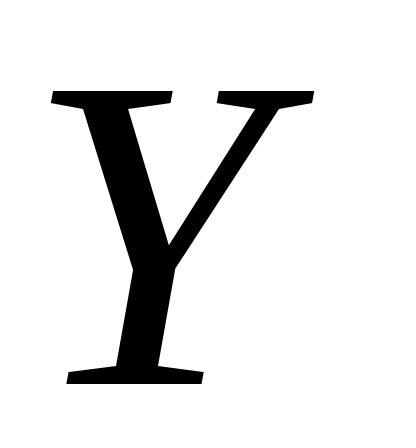
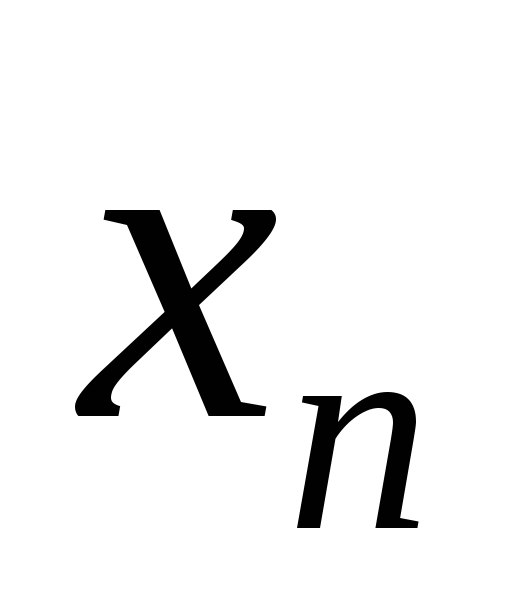
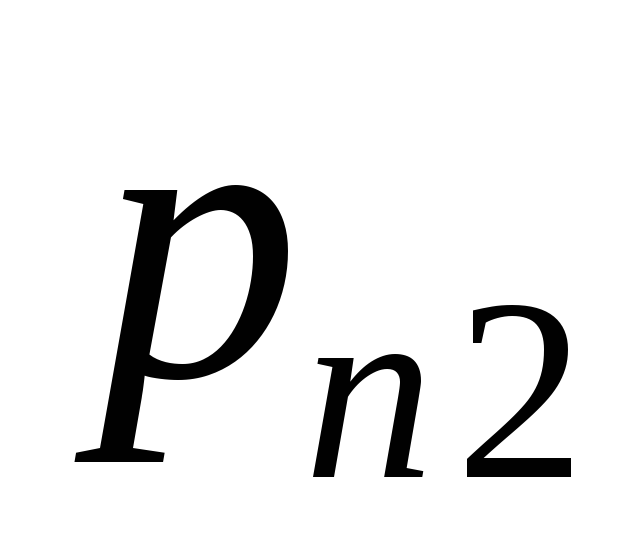
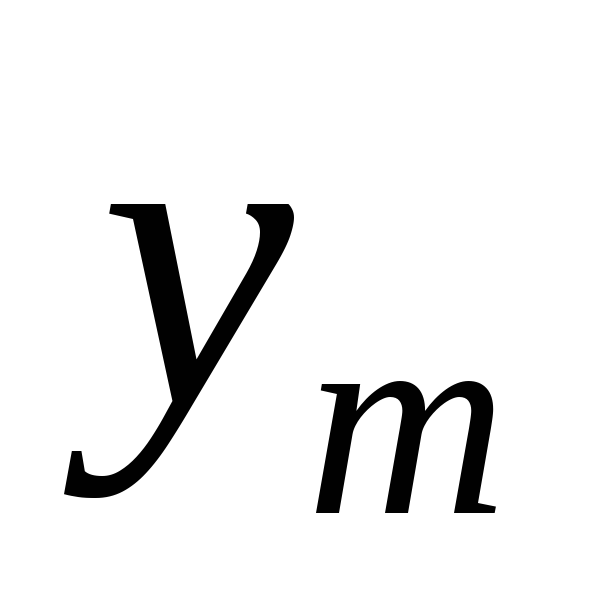
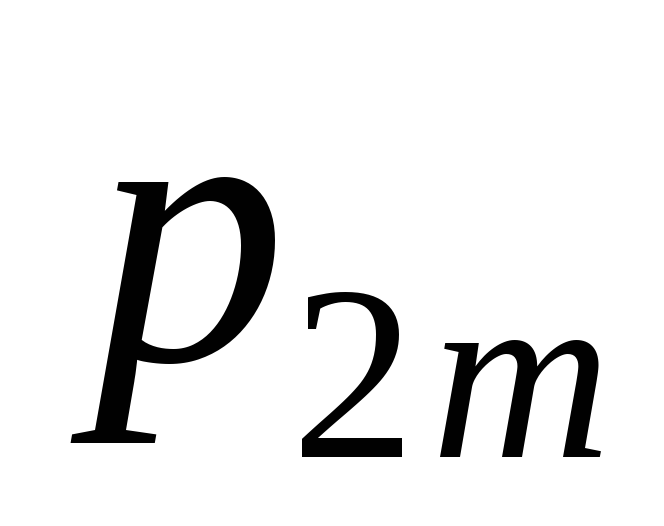
Т.к. события ,;образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы, равна единице.

Зная закон распределения двумерной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события ,, …,несовместны, поэтому по теореме сложения

.

Таким образом, для того, чтобы найти вероятность , надо просуммировать вероятности столбца. Аналогично, для того, чтобы найти вероятность, нужно просуммировать вероятности-ой строки.

Определение. Две случайные величины называютсянезависимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Теорема. Для того, чтобы случайные величиныибыли независимыми, необходимо и достаточно, чтобы функция распределения системыбыла равна произведению функций распределения составляющих:

.

Доказательство.

а) Необходимость. Пустьи– независимы. Тогда событияинезависимы. Следовательно, вероятность совмещения этих событий равна произведению вероятностей, т.е.

.

б) Достаточность.Пусть

и– независимые события, следовательно,и– независимые величины.

Следствие. Для того, чтобы непрерывные случайные величиныибыли независимыми, необходимо и достаточно, чтобы плотность распределения системыбыла равна произведению плотностей распределения составляющих:

.