10. Гармонические колебания. Действующие и амплитудные значения.

Гармонические колебания

Гармонические колебания — это периодические изменения физической величины, которые описываются синусоидальными функциями. В контексте электрических цепей гармоническими колебаниями являются синусоидальные изменения напряжения и тока.

Уравнение гармонического колебания

Гармоническое колебание может быть описано следующим уравнением

Действующие и амплитудные значения

Амплитудное значение

Амплитудное значение — это максимальное значение колеблющейся величины, которое она принимает за период:

A

Амплитуда характеризует наибольшее отклонение величины от среднего значения за полный период колебания.

Действующее значение

Действующее значение (также известное как среднеквадратичное значение, RMS — Root Mean Square) — это значение постоянного тока или напряжения, которое выделяет в сопротивлении такое же количество тепла, что и переменный ток или напряжение за тот же период времени.

Для синусоидального сигнала действующее значение определяется как:

Примеры расчетов

Пример 1: Синусоидальное напряжение

Рассмотрим синусоидальное напряжение с амплитудой A=10 В

Амплитудное значение: 10 В

Действующее значение:

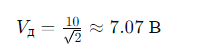
Пример 2: Синусоидальный ток

Рассмотрим синусоидальный ток с амплитудой A=5 А

Амплитудное значение: 5 А

Действующее значение:

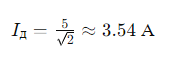
Значение действующих и амплитудных значений

• Амплитудное значение важно для понимания максимального отклонения величины от среднего значения. Это значение часто используется в теории колебаний и волновых процессов.

• Действующее значение важно для практических расчетов в электротехнике, так как именно это значение используется для определения мощности и нагрева в цепях переменного тока.

Фазовая диаграмма

Гармонические колебания также можно представить в виде фазовой диаграммы, где каждая синусоида представляется в виде вектора в комплексной плоскости. Амплитуда определяет длину вектора, а начальная фаза — угол вектора относительно оси времени.

Применение

• Электрические цепи: Анализ синусоидальных сигналов и расчёт мощности в цепях переменного тока.

• Механические системы: Описание колебательных движений, таких как колебания маятника или пружинных систем.

• Радиотехника: Обработка сигналов в передатчиках и приемниках.

Заключение

Гармонические колебания являются основой многих процессов в физике и технике. Понимание амплитудных и действующих значений позволяет эффективно анализировать и проектировать различные системы, от электрических цепей до механических колебательных систем.

11. Цепь переменного тока с последовательным соединением приемников. АГАРКОВ

Цепь переменного тока с последовательным соединением приемников

Дифференциальное уравнение цепи с последовательным соединением элементов R, L, C составленное по второму закону Кирхгофа, имеет вид

 t,

где   –  напряжение на резистивном элементе,   – напряжение на индуктивном элементе,   – напряжение на емкостном элементе.

    Если ток в цепи синусоидальный   , то напряжение на резистивном элементе   совпадает по фазе с током, напряжение на индуктивном элементе    опережает по фазе ток на 90°, напряжение на емкостном элементе   отстает по фазе от тока на 90°, Таким образом, мгновенное значение напряжения на входе цепи равно

 .

      Сумме синусоидальных напряжений соответствует сумма изображающих их векторов или сумма комплексных действующих напряжений.

 , или   .

      Это соотношение представляет собой уравнение цепи (рис. 1.1), составленное по второму закону Кирхгофа в комплексной форме. В этом уравнении

 ;   ;   .

      Из этого уравнения легко получается закон Ома в комплексной форме. Выражение, стоящее в знаменателе есть комплексное сопротивление      цепи с последовательным соединением элементов R, L, C.

 или   ,

где  R – активное сопротивление;   – реактивное сопротивление,   – индуктивное сопротивление,   – емкостное сопротивление.

      Комплексные величины в законе Ома могут быть записаны в показательной форме

 ,              ,

где   .

 ,   .

      Два комплексных числа равны друг другу, если равны их модули и равны их аргументы

 ;   .

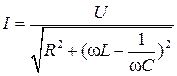      Полученное выражение 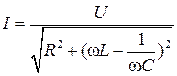   устанавливает связь между действующими током и напряжением.

      Выражение в знаменателе называется полным сопротивлением   ;   , откуда   .

      Если известны действующие напряжения   ,   ,   ,

то   ;   ;   .

      Из выражения связи между действующим током и напряжением   следует

                  , откуда   .

11. Мощность в цепях синусоидального тока.