51. Разностное уравнение и блок-схема.
Рекурсивные и нерекурсивные цепи. Устойчивость.
Разностное уравнение и блок-схема используются для описания и анализа дискретных систем. Разностное уравнение представляет математическую модель системы, тогда как блок-схема визуально демонстрирует структуру системы.
Разностное уравнение
Разностное уравнение описывает связь между входным сигналом x[n] и выходным сигналом y[n] дискретной системы. Оно может включать текущие и предыдущие значения этих сигналов.
Блок-схема
Блок-схема иллюстрирует, как компоненты дискретной системы соединены между собой. Она включает узлы, представляющие операторы задержки, коэффициенты и сумматоры.
Рекурсивные и нерекурсивные цепи
Дискретные системы можно классифицировать как рекурсивные (с обратной связью) и нерекурсивные (без обратной связи) в зависимости от наличия или отсутствия обратной связи в системе.
Рекурсивные цепи
Рекурсивные цепи содержат элементы обратной связи. В этих цепях текущее значение выходного сигнала зависит не только от текущего значения входного сигнала, но и от предыдущих значений выходного сигнала. Пример разностного уравнения для рекурсивной цепи:
Нерекурсивные цепи
Нерекурсивные цепи не содержат элементов обратной связи. В этих цепях текущее значение выходного сигнала зависит только от текущего и предыдущих значений входного сигнала. Пример разностного уравнения для нерекурсивной цепи:
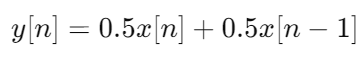
Устойчивость дискретных систем
Устойчивость дискретной системы означает, что на ограниченный входной сигнал система даёт ограниченный выходной сигнал. В математическом смысле, система устойчива, если её выходное значение остаётся ограниченным для любого ограниченного входного значения.
Условия устойчивости
Для рекурсивных систем: Устойчивость рекурсивной системы определяется корнями её характеристического уравнения. Система устойчива, если все корни характеристического уравнения находятся внутри единичного круга в комплексной плоскости.
2. Для нерекурсивных систем: Нерекурсивные системы всегда устойчивы, так как они не содержат обратной связи. В таких системах выходной сигнал является конечной суммой конечного числа входных значений, что автоматически гарантирует устойчивость.