Основные определения

1. Оригинал — последовательность , удовлетворяющая условию: , где M и σ — положительные постоянные

2. Изображение последовательности — функция F(z) комплексного переменного z, определяемая равенством

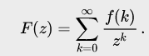
Изображение является аналитической функцией при

Совокупность всех оригиналов называется пространством оригиналов, а совокупность всех изображений — пространством изображений.

3. Переход, определяющий изображение F(z) по оригиналу , называется Z-преобразованием:

4. Оригинал по изображению находится с помощью обратного Z-преобразования по формуле: где C — контур, внутри которого лежат все особые точки функции F(z).

Замечания

1. Название Z-преобразование определяется буквой z, выбранной для обозначения переменной. Такое название противоречит существующему обычаю называть часто применяемые преобразования по имени ученого. В некоторых источниках Z-преобразование называется преобразованием Лорана, так как ряд дает разложение функции F(z) в ряд Лорана в окрестности бесконечно удаленной точки.

2. Z-преобразование можно рассматривать как частный случай преобразования Лапласа, а именно как преобразование в пространстве ступенчатых оригиналов. Ступенчатая функция — это разрывная функция целочисленного аргумента, которая в общем случае имеет разрывы при каждом натуральном значении аргумента, оставаясь между ними постоянной.

Тогда по теореме запаздывания т.е. нахождение преобразования Лапласа в рассматриваемом классе оригиналов сводится к нахождению суммы ряда Тейлора:

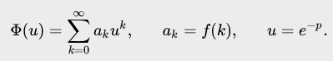
Свойства Z-преобразования

Положим, что .

1. Линейность. Для любых постоянных справедливо

где — оригиналы, a — их изображения.

2. Запаздывание (формула запаздывания), где при

3. Опережение (формула опережения):

4. Дифференцирование изображения:

5. Умножение изображений. Свертке оригиналов соответствует произведение изображений:

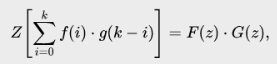где G(z)=Z[g(k)]. Сверткой оригиналов и называется сумма

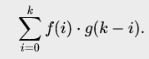
6. Теоремы о предельных значениях. Если , то

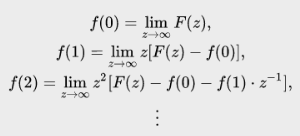
Где z стремится к бесконечности вдоль произвольного пути. Если существует, то

Таблица Z-преобразований

50. Импульсная характеристика дискретной цепи. Передаточная функция.

Дискретные системы - называются системы, у которых входные, промежуточные и выходные сигналы определены для некоторых дискретных моментов времени на заданном временном интервале.

Импульсная характеристика дискретной цепи

Импульсная характеристика h[n] дискретной цепи — это отклик системы на единичный импульс δ[n]. Она представляет собой последовательность значений, которые выход дискретной системы принимает в ответ на единичный импульс на входе. Импульсная характеристика является фундаментальной характеристикой, которая полностью описывает линейную стационарную дискретную систему во временной области.

Определение импульсной характеристики

Если на вход системы подать единичный импульс δ[n], то на выходе системы мы получим её импульсную характеристику h[n]. Это можно записать следующим образом:

Передаточная функция - отношение выходного напряжения к входному напряжению.