47. Аналоговые и дискретные сигналы. Дискретное преобразование Фурье.
Дискретное преобразование Фурье (ДПФ) является ключевым инструментом в анализе сигналов и обработке данных. Оно позволяет переводить сигнал из временной области в частотную, раскрывая его составляющие частоты.
ДПФ преобразует последовательность N значений временного сигнала в последовательность N значений частотного спектра. Это математическое преобразование вычисляет амплитуду и фазу каждой частотной компоненты в сигнале.
ДПФ широко используется в области сигнальной обработки, включая аудио и видеообработку, радиосвязь, медицинскую обработку сигналов и многое другое.
Дискретное преобразование Фурье (ДПФ) - это метод анализа сигналов в дискретном времени, который разбивает сигнал на составляющие частоты. Это полезно для анализа и обработки сигналов в цифровой форме, например, в обработке звука, изображений, видео и телекоммуникациях.
48. Аналоговые и дискретные сигналы. Быстрое преобразование Фурье:
Основная идея БПФ состоит в делении исходного N-точечного дискретного преобразования Фурье на два и более меньших (по длине) преобразований, каждое из которых можно вычислить отдельно, а затем линейно просуммировать с остальными, что в итоге дает преобразование исходной последовательности.
Для вычисления одного спектрального отсчета требуется (3.13) N операций комплексного умножения и сложения, поэтому общая вычислительная сложность данного преобразования оценивается в N2 комплексных умножений и сложений. Если заменить одно преобразование на N точек двумя преобразованиями на N/2 точек каждое, то это приведет к сокращению числа необходимых операций в 2 раза. Схематично данная процедура разбиения представлена на рис.3.9.
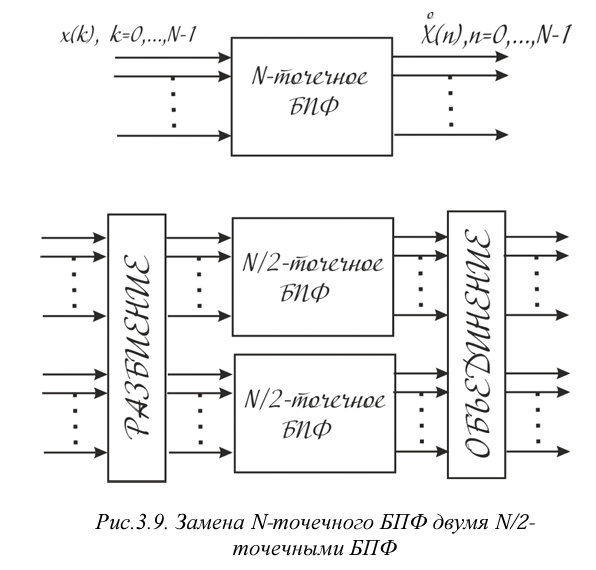
Процедура разбиения может быть продолжена далее и каждое из N/2-точечных преобразований может быть на пару N/4-точечных БПФ и т.д. Если N=2n, то такое разбиение может быть проведено n раз. Алгоритмы БПФ, которые используют выборки длиной N=2n, называются «алгоритмы БПФ по основанию 2». Данные алгоритмы получили наибольшее распространение, из-за удобства применения в машинной арифметике. Очевидно, что делить последовательности на две можно по-разному, однако от этого зависит сможем ли мы при объединении получить неискаженный спектр сигнала и чего с точки зрения вычислительных затрат это будет нам стоить. Эффективность алгоритма БПФ полностью зависит от способа разбиения и объединения последовательности, поскольку если не учитывать операции на разбиение-объединение, то для расчета спектра требуется N/2 раз посчитать ДПФ на 2 точки, в результате общее количество вычислительных операций составит 22N/2=2N, то есть количество операций линейно зависит от величины выборки.
В общем случае вычисление N-точечного БПФ требует выполнения примерно 𝑁log2(𝑁) шагов с операциями сложения и 𝑁log2(𝑁)/2 операциями умножения на каждом шаге, что значительно меньше требуемых 𝑁2 операций необходимых для вычисления обычного дискретного преобразования Фурье для последовательности той же длины. Существует два основных способа разбиения — объединения: прореживание по времени и прореживание по частоте. По указанным выше причинам в данном курсе мы не будем подробно их рассматривать, но желающие могут ознакомиться с ними самостоятельно, так как подобные описания широко представлены в литературе.
В методе быстрого преобразования Фурье кривая делится на большое число равномерно распределённых выборочных значений. Количество умножений, необходимое для анализа кривой, уменьшается наполовину при таком же уменьшении количества точек.
Например, кривая с 16 выборочными значениями обычно требует 16 в квадрате, или 256 умножений. Но предположим, что кривая была поделена на два интервала, по 8 точек в каждом. В этом случае количество умножений, требующихся для анализа каждого интервала, равно 82, или 64. В сумме для обоих интервалов получаем 128, или половину от исходного количества.
49. Z-преобразование и его свойства: