41. Длинные линии. Волновое сопротивление линии с потерями и без потерь. Коэффициент распространения. Длина волны и фазовая скорость.

Длинные линии – простейшие модели электрических цепей с распределенными элементами, учитывающих распределение элементов вдоль только одной координаты. Несмотря на простоту таких моделей, уравнения длинных линий играют фундаментальную роль в теории волновых процессов. Они позволяют описывать волновые процессы и явления, происходящие как в различных линиях передачи (двухпроводных, коаксиальных, полосковых), так и в системах, основанных на распространении волн в активных и нелинейных средах.

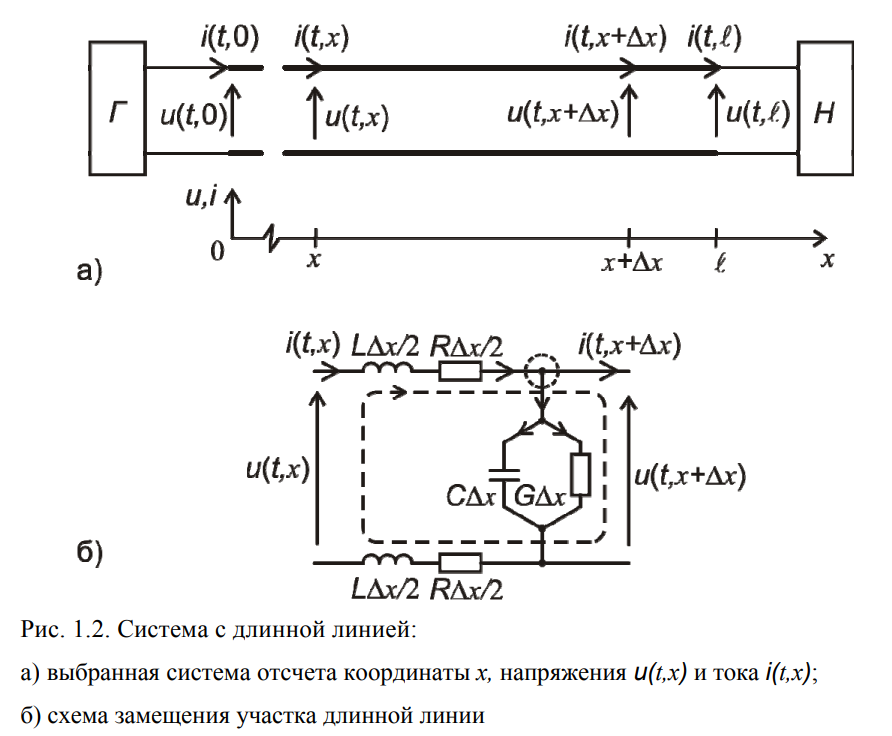
Рассматривая линейную однородную инвариантную во времени длинную линию, выберем в ней участок, размер которого Δх удовлетворяет неравенству Δх << λ. Сопоставим ему схему замещения, содержащую указанные распределенные элементы (рис. 1.2б). Используя законы Кирхгофа для контура, помеченного пунктиром, и для верхнего узла, запишем систему уравнений:

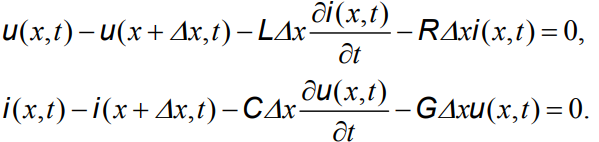
Устремляя Δх → 0, получим уравнения длинных линий (телеграфные уравнения) – систему двух дифференциальных уравнений в частных производных, связывающую токи и напряжения в произвольном сечении линии. В рассматриваемом случае инвариантной во времени линии эта система имеет вид:

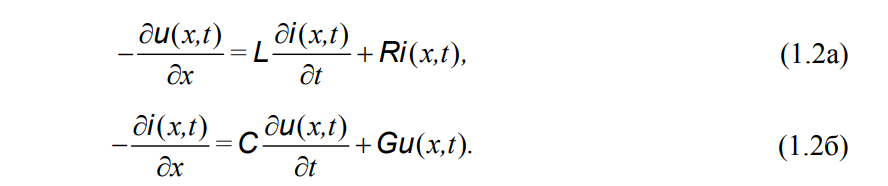
Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь. Линия без потерь – это линия, у которой рассеяние энергии отсутствует, что имеет место при значениях первичных параметров R = 0 и G =0.

Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радиотехнических устройств, полосковых линий, измерительных линий, согласующих СВЧ устройств и др.), где выполняются условия R   wL и g   wC и поэтому резистивными сопротивлением проводов и проводимостью изоляции можно пренебречь по сравнению с индуктивным сопротивлением и емкостной проводимостью линии.

Коэффициент распространения — это параметр, который характеризует изменение амплитуды и фазы бегущей электромагнитной волны при её перемещении на единицу длины линии.

Коэффициент распространения линии без потерь

Отсюда коэффициент ослабления a = 0, а коэффициент фазы b = w   линейно зависит от частоты.

Волновое сопротивление линии без потерь является чисто активным (резистивным).

Коэффициент фазы b связан с длиной волны электромагнитного колебания. Длиной волны l называется расстояние между двумя точками, взятыми в направлении распространения волны, фазы в которых отличаются на 2p. Следовательно, bl = 2p и l = 2p/b.

Длина волны и фазовая скорость.

Минимальное расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны.

Длиной волны   называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна  ).

Если точки разделены расстоянием  , их колебания происходят в противофазе.

Фазовая скорость волны

Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой.

Фазовая скорость   - это скорость распространения данной фазы колебаний, т.е. скорость волны.

Связь длины волны  , фазовой скорости   и периода колебаний Т задается соотношением:

.

Учитывая, что  , где   - линейная частота волны,   - период, а циклическая частота волны  , получим разные формулы для фазовой скорости:

.

Для волнового процесса характерна периодичность по времени и по пространству.

Т – период колебаний точек среды. Роль пространственного периода играет длина волны  . Соотношение между периодом и циклической частотой задается формулой:  . Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом:  .

Таким образом. Можно добавить еще одно уравнение для фазовой скорости:

.

Фазовая скорость различна для разных сред

В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:

 ,

где  - модуль сдвига среды,   -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Фазовая скорость упругих продольных волн в твердом теле равна

,

где Е - модуль Юнга,  - плотность невозмущенной среды (твердого тела до момента распространения по нему волны).

Фазовая скорость продольных волн в жидкости и газе определяется соотношением:  ,

где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема,  - плотность невозмущенной среды.

Фазовая скорость продольных волн в идеальном газе задается формулой:  ,

 - показатель адиабаты,  - молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа ( ) и от его термодинамического состояния (Т).