27. Резонанс. Последовательный колебательный контур
Резонанс в электрических цепях — это явление, при котором реактивные элементы цепи (катушки индуктивности и конденсаторы) взаимодействуют таким образом, что возникают особенные электрические условия. Резонанс происходит, когда частота внешнего источника напряжения или тока соответствует собственной частоте колебаний системы.
В результате резонанса возникает увеличение амплитуды колебаний тока или напряжения в цепи. Это явление может быть использовано для создания резонансных фильтров, антенн, усилителей и других устройств. Однако резонанс также может привести к нежелательным эффектам, таким как перегрузка и повреждение элементов цепи.
Резонанс в электрических цепях может быть классифицирован на серийный и параллельный, в зависимости от того, как соединены индуктивность и ёмкость в цепи.
Последовательный колебательный контур в электрических цепях представляет собой комбинацию элементов, соединенных последовательно, которые создают возможность для колебаний электрического тока или напряжения на определенной частоте. Этот тип контура обычно состоит из резистора, индуктивности (катушки) и конденсатора, соединенных в последовательности.
При подаче переменного тока на такой контур происходит периодическое хранение и высвобождение энергии в индуктивности и конденсаторе, что приводит к колебаниям тока или напряжения в контуре. Частота этих колебаний зависит от параметров контура, таких как индуктивность и емкость, и может быть регулируемой
Последовательный колебательный контур состоит из индуктивности (L), емкости (C) и сопротивления (R), соединенных последовательно. Когда такая цепь подключается к переменному току, она может проявлять резонанс - явление, при котором амплитуда колебаний в контуре становится максимальной при определенной частоте сигнала.
Резонанс в последовательном колебательном контуре происходит, когда реактивные сопротивления (индуктивность и емкость) в точности компенсируют друг друга, что приводит к резкому увеличению амплитуды колебаний в контуре. Это происходит при частоте, равной резонансной частоте контура, которая определяется его параметрами (L, C и R).
Таким образом, резонанс и последовательный колебательный контур тесно связаны через явление увеличения амплитуды колебаний при определенной частоте переменного тока
28. Резонанс. Параллельный колебательный контур.
Резонанс в параллельном колебательном контуре
Резонанс — это явление, при котором амплитуда вынужденных колебаний в системе становится максимальной при определенной частоте внешнего воздействия, называемой резонансной частотой. В электрических цепях резонанс может возникать как в последовательных, так и в параллельных контурах.
Параллельный колебательный контур
Параллельный колебательный контур состоит из параллельно соединенных индуктора L и конденсатора C. Эта схема обладает особым свойством, заключающимся в том, что при определенной частоте внешнего напряжения ток через контур минимален, а напряжение на элементах контура максимально.
Структура и уравнения
Параллельный колебательный контур можно описать следующим образом:
Индуктор L
Конденсатор C
Если к контуру приложено переменное напряжение V с частотой ω то комплексные сопротивления индуктора и конденсатора будут:
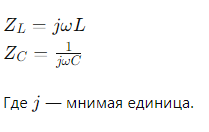
Адмиттанс параллельного контура
Адмиттанс Y
параллельного контура (обратная величина
импеданса) определяется как:
Резонансная частота
Резонансная частота ω0 — это частота, при которой реактивные сопротивления индуктора и конденсатора равны по модулю, но противоположны по знаку:
На этой частоте:
Импеданс контура становится максимальным.
Адмиттанс минимален.
Ток через источник минимален, так как большая часть тока циркулирует между L и C.
Реактивные токи
На резонансной частоте индуктор и конденсатор создают противоположные реактивные токи, которые компенсируют друг друга, что приводит к минимальному току через источник. Однако токи через индуктивность и ёмкость могут быть значительными, что приводит к высокому напряжению на элементах контура.
Добротность параллельного контура
Добротность Q параллельного колебательного контура характеризует степень затухания колебаний и определяется как:
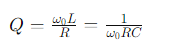
Где R — это суммарное сопротивление потерь в контуре.
Пример
Рассмотрим параллельный контур с индуктивностью L=1 Гн и ёмкостью C=1 мкФ
Вывод
Параллельный колебательный контур имеет важное значение в радиотехнике и других областях, где необходимо выборочно усиливать или фильтровать сигналы определенной частоты. На резонансной частоте параллельный контур характеризуется минимальным током через источник и максимальным напряжением на элементах индуктора и конденсатора.