Лабы Механика Спиридонов

Упражнение 2. Изучение колебаний маятников в режиме биений.

1. Задайте режим колебаний, соответствующий наиболее выраженным биениям: один ма-

ятник удерживайте в положении равновесия, а другой отклоните на угол 5...10 , а затем одновременно отпустите маятники.

2. Когда колебательный процесс стабилизируется, запустите программу измерений и записывайте колебания в течение 2 - 3 мин. При этом на экране монитора будут отображаться графики зависимостей 1(t) и 2 (t) , каждый из которых имеет форму биений. Графики биений

маятников «сдвинуты» по времени, так что в моменты, когда амплитуда колебаний одного маятника максимальна, амплитуда другого минимальна, и наоборот. При этом происходит периодическая (с периодом TБ ) «перекачка» энергии колебаний от одного маятника к другому.

3.Определите по графикам период биений TБ (см. рис.1) и его погрешность. Для повышения точности используйте инструменты «Обзор» и «Лупа» (см. приложение 2).

4.Найдите частоту биений Б 1/TБ и ее погрешность, сравните полученный результат с

величиной 2 1 , рассчитанной по результатам измерений частот противофазных и синфаз-

ных колебаний.

Полученные результаты сведите в табл.2.

Таблица 2

Результаты эксперимента

Упражнение 3. Исследование зависимости частоты биений от положения пружины, «связывающей» маятники.

Измените расстояние b (см. рис.2) в n (0,7...1,5) раза ( b nb ), и измерьте соответст-

вующее значение частоты биений 'Б . Покажите, что в согласии с формулой (9) 'Б / Б n2 .

Сформулируйте выводы по результатам работы. Основные результаты измерений све-

дите в табл.3.

121

Подготовка к работе

1.Физические понятия, законы:гармонические колебания;

амплитуда, фаза, начальная фаза, период, частота, циклическая частота;дифференциальное уравнение гармонических колебаний;сложение гармонических колебаний, биения;

математический и физический маятники, собственная частота колебаний;колебания связанной системы.

2.Приведите в конспекте подробный вывод формул (5) - (7).

3.Расчетное задание.

По формулам (8) рассчитайте зависимости 1(t) и 2 (t) в режиме биений. Величину b выберите в соответствии с индивидуальным заданием (см. табл.1). При расчетах примите: m = 1 кг, l = 1 м, k = 3 Н/м. Постройте графики 1(t) и 2 (t) , используя любую доступную

компьютерную программу построения графиков (например, http://www.yotx.ru/default.aspx). График вклейте в конспект.

4. Сформулируйте цель работы и порядок ее выполнения.

П р и м е ч а н и е. Пункты 2 - 4 выполните письменно при подготовке к лабораторной работе.

Рекомендуемая литература

1.Иродов И.Е. Механика. Основные законы. - М.: БИНОМ. Лаборатория знаний, 2013. - 309 с.

§5.4; 6.1 - 6.4.

2.Савельев И.В. Курс общей физики: в 4 т. Т.1. Механика. Молекулярная физика и термодинамика:

учеб. пособие / Под общ. ред. И.В. Савельева. - М.: КНОРУС, 2009. - 528 с. § 5.3; 5.4; 8.1; 8.4; 8.6; 8.7; 8.9; 8.11.

122

Приложение 1

Вывод формул (5) - (9)

При малых углах отклонения маятников от вертикали ( 1 1 , 2 1 , см. рис.2) ось пружины при колебаниях остается практически горизонтальной (рисунок). В этом случае суммарный

Полученные выражения для моментов сил подставим в уравнения динамики вращательного движения маятников:

где 1 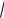g / l ; D kb2 / ml2 .

Заметим, что величина 1 равна собственной частоте уединенного (несвязанного) маятни-

ка, а величина D зависит от параметров маятника и пружины, ее называют коэффициентом связи системы.

Складывая уравнения системы (П1), получим:

где 1 1 2 .

123

Общее решение этого уравнения имеет вид

Вычитая из второго уравнения системы (П1) первое, получим:

где 2 2 1 ; 22 12 2D .

Общее решение этого уравнения имеет вид

124

Приложение 2

Измерение собственных частот колебаний связанных маятников

1.В меню «Прибор» компьютерной программы выберите диалоговое окно «Универсальный измеритель».

2.В появившемся диалоговом окне наберите показанные на рис.П2.1 установки.

Рис.П2.1. Диалоговое окно «Универсальный измеритель»

3. Сняв и поставив флажки в окошках «Аналоговый дисплей» и «Диаграмма», активируйте на экране окна, изображенные на рис.П2.2. Эти окна предназначены для установки максимального угла отклонения маятника от вертикали на аналоговом приборе и для выбора каналов, отображаемых на диаграмме.

125

6. Для измерения частот синфазных колебаний маятников отклоните их на одинаковые углы 5 - 10 (контролируются приборами, изображенными на рис.П2.3) в одну сторону от вертикали и одновременно отпустите. Измерения начинайте примерно через 30 с после начала колебаний, когда колебательный процесс установится. Запись колебаний должна происходить не менее двух-трех минут. После завершения измерений на экране отображаются графики колебаний. Выбирая входы 1 или 2, путем нажатия на кнопки U1 или U2, можно наблюдать на экране монитора графики колебаний каждого маятника в отдельности или сразу оба графика. Для одинаковых маятников и одинаковых начальных условий кривые 1(t) и 2 (t) должны практически совпадать. Если кривые не совпадают, обратитесь к инженеру или преподавателю.

7. Определите по графикам период синфазных колебаний T1 , пользуясь для повышения точности инструментами «Обзор» и «Лупа» (рис.П2.4). Оцените случайную погрешность измерения T1 , воспользовавшись рекомендациями, приведенными в описании лабораторной рабо-

ты №1. Приборная погрешность измерения времени в данных экспериментах не превышает

200 мс. При необходимости проконсультируйтесь с преподавателем или инженером.

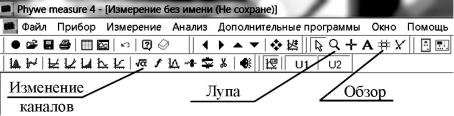
Рис.П2.4. Инструменты «Лупа» и «Обзор» для измерения периода колебаний

8. Аналогичным образом определите период T2 противофазных колебаний, отклоняя ма-

ятники на равные углы в противоположные стороны от положения равновесия.

9. Рассчитайте собственные частоты (частоты синфазных и противофазных колебаний) и

их погрешности: 1,2 1/T1,2 , 1,2 T1,2 , 1,2 1,2 1,2 .

127

Лабораторная работа № 12

Уравнение состояния идеального газа

Цель работы: экспериментальное изучение законов идеального газа на примере воздуха; исследование изотермического и изохорного процессов.

Оборудование: установка, включающая газовый шприц в стеклянном корпусе, нагреватель, датчик давления, датчик температуры, блок управления «Cobra3», компьютер.

Продолжительность работы: 4 часа.

Теоретическая часть

Согласно современным молекулярно-кинетическим представлениям вещество состоит из малых частиц - молекул. Молекулы взаимодействуют друг с другом посредством молекулярных сил. С этими силами связано слабое притяжение молекул на далеких расстояниях и их отталкивание на расстояниях, сравнимых с размером молекулы. Молекулы находятся в постоянном движении. Если вещество в целом находится в покое, не взаимодействует с другим веществом, то в результате столкновений установится хаотическое движение, при котором все направления движения равновероятны. Хаотическое движение молекул называется тепловым движением, его интенсивность определяет температуру вещества. О тепловом движении можно говорить только в том случае, если рассматриваемое вещество - это система, состоящая из очень большого числа молекул. Такая система называется макроскопической.

Макроскопическая система может находиться в различных термодинамических состояниях. Эти состояния характеризуются макроскопическими параметрами, которые могут быть получены в результате измерений. К макроскопическим параметрам относятся объем V , давление p ,

температура T , количество вещества и др. В равновесном состоянии эти параметры имеют определенное и постоянное значение в любой части системы1. Состояние, в котором хотя бы один из параметров зависит от координат и (или) от времени, является неравновесным.

Одним из важных макроскопических параметров является количество вещества . Единицей измерения количества вещества является моль. Моль - это количество вещества, в котором содержится число частиц, равное числу атомов в 0,012 кг изотопа углерода 12С. Опытным путем установлено, что это число равно

NA 6,02213 1023 моль 1 .

Величина NA называется постоянной Авогадро. Если m - масса вещества, N - число молекул, - молярная масса (масса одного моля), то количество молей равно

N NА m .

1 За исключением всегда существующих флуктуаций.

128

Вгазах при условиях, близких к нормальным2, средние расстояния между молекулами велики по сравнению с их характерным размером. На таких расстояниях молекулярные силы слабы и не играют существенной роли. Они проявляются лишь на расстояниях порядка размера молекулы. Под действием этих сил скорости молекул при столкновениях меняются по модулю

ипо направлению, а между двумя последовательными столкновениями молекулы газа двигаются практически свободно. Чем более разрежен газ, тем длиннее средний путь, проходимый молекулой между столкновениями. Для достаточно разреженного газа в первом приближении можно пренебречь размерами молекул и их взаимодействием друг с другом на расстоянии. Такая простейшая модель приводит к законам идеального газа.

Идеальный газ - теоретическая модель газа, в которой пренебрегают размерами и взаимодействиями частиц газа и учитывают лишь их упругие столкновения. Законы идеального газа - приближенные законы. Реальные газы хорошо описываются законами идеального газа, если они достаточно разрежены и находятся при температуре, далекой от температуры конденсации.

Давление газа на стенку сосуда обусловлено большим количеством ударов его молекул. При каждом ударе молекулы о стенку изменяется импульс молекулы. Следовательно, на молекулу со стороны стенки действует сила. Такая же по величине, но противоположно направленная сила действует на стенку со стороны молекулы. Если бы в сосуде было всего несколько молекул, то стенка испытывала отдельные бесконечно малые толчки. При очень большом числе молекул малые силы отдельных ударов складываются в конечную, почти постоянную силу. Эта сила, усредненная по времени, и есть давление газа.

Вмолекулярно-кинетической теории для давления идеального газа выводится следующее уравнение:

При выводе уравнения (1) молекулы рассматриваются как бесструктурные материальные точки. В действительности при столкновении молекулы могут переходить в возбужденное состояние, могут меняться скорости их вращения. Однако эти процессы не играют роли при вычислении давления газа: важно только то, что изменяется импульс молекул. В уравнении (1) под символом следует понимать скорость поступательного движения центра масс молекулы. Уравнению (1) можно придать вид

где пост m0 2 2 - средняя кинетическая энергия поступательного движения молекул.

Уравнение (2) называется основным уравнением молекулярно-кинетической теории.

Температура - одна из характеристик внутреннего состояния макроскопической системы. Она не имеет смысла для систем, состоящих из небольшого числа молекул. Существует два определения температуры: одно использует термодинамический подход, другое - молекулярно-

2 По определению при нормальных условиях атмосферное давление p0 = 101325 Па, температура T0 = 273,15 K. По закону Авогадро при нормальных условиях один моль любого идеального газа занима-

ет объем V0 22,414 10 3 м3.

129

кинетический. В термодинамике понятие температуры вводится как характеристика степени нагретости вещества. Строгое определение понятия «более (менее) нагретое» вещество использует понятие энергии. Если при установлении теплового контакта между двумя макроскопическими системами одна из них передает энергию другой, то передающая система имеет большую температуру. Когда обмен энергией прекращается, это означает, что обе системы имеют одинаковую степень нагретости, т.е. одинаковую температуру. Говорят, что они находятся в тепло-

вом равновесии.

При молекулярно-кинетическом подходе к определению температуры доказывается, что для нескольких макросистем, находящихся в тепловом равновесии, средняя кинетическая энер-

гия пост всех молекул одинакова. Таким образом, величина пост является мерой температуры. По определению за температуру принимают величину

Величина Θ называется энергетической или кинетической температурой. Она измеряется в джоулях, и для установления такой температурной шкалы не требуется каких-либо специальных эталонов и договоренностей.

Однако оказалось удобным использовать в качестве единицы измерения температуры градус Цельсия. Температурная шкала Цельсия, получившая распространение еще до развития мо- лекулярно-кинетической теории, использует две реперные точки: температуру таяния льда и температуру кипения воды при нормальном давлении. Одна сотая этого температурного диапазона принята за градус Цельсия. Перевод температуры в энергетических единицах в температу-

абсолютной температурой, она по определению всегда положительна и отсчитывается от нуля (абсолютного нуля температуры). За единицу измерения абсолютной температуры принят кельвин (K), совпадающий по величине с градусом Цельсия.

Из уравнений (3) и (4) следует, что средняя кинетическая энергия поступательного движения молекулы равна

Это уравнение называется уравнением состояния идеального газа. Если в объеме V содержится N NA молекул газа, то n NA V . Подставив n в уравнение (6), получим:

pV NA kT .

3 URL: http://physics.nist.gov/cuu/Constants/Table/allascii.txt

130