Односторонний предел по Коши

• Число  называется правосторонним пределом (правым пределом, пределом справа) функции  в точке , если для всякого положительного числа  отыщется отвечающее ему положительное число  такое, что для всех точек  из интервала  справедливо неравенство .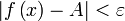

• Число 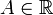 называется левосторонним пределом (левым пределом, пределом слева) функции  в точке , если для всякого положительного числа  отыщется отвечающее ему положительное число  такое, что для всех точек  из интервала  справедливо неравенство .

16

(локальные свойства непрерывных функций).

1. Пусть функция f:E R непрерывна в точке a. Тогда f(x) ограничена в некоторой окрестности точки a.

2. Пусть функция f(x) непрерывна в точке a и f(a) 0, то в некоторой окрестности точки a все значения функции положительны или отрицательны вместе с f(a).

3. Если f(x), g(x) - непрерывны в точке a, то функции: f(x)+g(x), f(x)g(x), f(x)/g(x) (при g(a) 0 ) непрерывны в точке a.

4. Если функция g(x):Y R непрерывна в точке b Y, а функция f:E Y непрерывна в точке a, f(a) = b, тогда композиция g_° f также непрерывна в точке a.

Функция называется непрерывной на множестве, если она непрерывна в каждой точке множества.

То, что f(x) непрерывна на множестве X обозначается следующим образом: f(x)C_X.

Определение 27. Функция называется непрерывной на отрезке [a,b] , если она непрерывна в каждой внутренней точке этого отрезка и непрерывна справа в точке a и непрерывна слева в точке b.

То, что f(x) непрерывна на отрезке [a,b] обозначается следующим образом: f(x)C_[a,b].

Перечислим основные глобальные свойства непрерывных функций.

Теорема 10 (глобальные свойства непрерывных функций).

1. (Первая теорема Вейерштрасса) Если функция f(x) C_[a,b], то онаограничена на [a,b] (см. рис. 18).

2. (Вторая теорема Вейерштрасса) Если f(x) C_[a,b], то она достигает на [a,b] своих точных верхней и нижней граней (рис. 19)

3. (Теорема Коши) Если f(x) C_[a,b] и f(a)f(b)<0, то существует c [a,b] f(c) =0 (см.рис. 20).

Замечание.

1. Функции, не являющиеся непрерывными на данном отрезке, могут принимать точную верхнюю и точную нижнюю грани, например функция Дирихле.

2. Если в условиях теоремы отрезок заменить на интервал, то теорема будет неверна, например, функция 1/x на интервале (0,1) непрерывна, но не является ограниченной; функция y = x на интервале (0,1) не достигает своих точных граней.

Пример 25. Исследовать на непрерывность в точке x = 0 и установить характер разрыва функции в этой точке:

1. f(x) = 1/(1+2^1/x)

Решение.

lim_x -01/(1+2^1/x) = 1 lim_x +01/(1+2^1/x) = 0,

так как

lim_x +02^1/x = , lim_x -02^1/x = 0.

Следовательно, f(x) в точке x = 0 имеет разрыв первого рода.

2. f(x) =

    (1/5)(2x2+3), при -<x1,  6-5x, при 1<x<3,  x-3, при 3 x<

3. Решение. Заметим, что на интервалах (-,1), (1,3), (3,) функция непрерывна. Поэтому разрывы возможны лишь в точках x = 1, x = 3, в которых изменяется аналитическое задание функции.

4. lim_x 1-01/5(2x2+3) = 1; lim_x 1+0(6-5x) = 1; f(1) = 1.

5. Таким образом в точке x = 1 функция непрерывна. Так как

6. lim_x 3-0(6-5x) = -9; lim_x 3+0(x-3) = 0,

7. то точка x = 3 - точка разрыва первого рода.

Упражнение 2. Исследовать на непрерывность

1. f(x) =

    e1/x, при x0,   0, при x = 0;

2. f(x) = E(x)- целая часть числа;

3. f(x) = arctg 1/(x-5) в точке a=5;

f(x) =

 x+2, при x<2,   x2-1, при x2.

17

В этом разделе мы на основе изученных выше свойств бесконечно малых величин (то есть функций, имеющих предел, равный 0) выясним свойства функций, имеющих произвольное значение предела.

        Теорема 2.8   Пусть функции  и  имеют пределы при одной и той же базе  :

Тогда функция  также имеет предел при базе , и этот предел  равен сумме пределов слагаемых:

        Доказательство.     Равенство  означает, в соответствии с теоремой 2.4, что величина -- бесконечно малая; равенство -- что -- бесконечно малая. Поэтому по теореме 2.5 сумма

также является бесконечно малой. Теорема 2.4 утверждает, что тот факт, что разность  бесконечно мала, означает, что ; это и требовалось доказать.      

        Замечание 2.2   В доказанной теореме не утверждается, что если существует предел суммы, то существуют и пределы слагаемых. Это неверно, что показывает простейший пример: пусть  и . Тогда  и предел , в то время как пределы при  функций  и  не существуют.

Так что из несуществования пределов слагаемых не следует несуществование предела суммы.     

        Теорема 2.9   Пусть функции  и  имеют пределы при одной и той же базе  :

Тогда функция  также имеет предел при базе , и этот предел  равен произведению пределов сомножителей:

        Доказательство.     Равенство  означает, в соответствии с теоремой 2.4, что величина -- бесконечно малая; равенство -- что -- бесконечно малая. Поэтому  и , откуда

или

Покажем, что в правой части этого равенства стоит бесконечно малая величина. Величина  -- бесконечно малая согласно следствию 2.3, а величина  -- бесконечно малая по теореме 2.7 (величина  имеет предел, равный 0, и, следовательно, локально ограничена по теореме 2.6). Поскольку разность между функцией  и постоянной  бесконечно мала при базе , то по теореме 2.4 ; это и требовалось доказать.      

        Замечание 2.3   Сделаем замечание, аналогичное замечанию 2.2: если существует предел произведения, то отсюда не следует, что существуют пределы каждого из сомножителей; доказанная теорема этого не утверждает. Приведём пример, который был уже разобран выше: функция  при  имеет предел, равный 0, однако предела  при  не существует (хотя другой множитель, , имеет предел при этой базе).

Так что из несуществования предела у какого-нибудь сомножителя не следует несуществование предела произведения.     

        Следствие 2.4   Пусть  и  (то есть -- постоянная величина). Тогда существует предел функции , равный :

        Доказательство.     Для доказательства достаточно заметить, что, согласно примеру 2.4, , и применить теорему 2.9.      

Доказанное следствие означает, что постоянный множитель  можно выносить за знак предела, а также вносить под знак предела. Иными словами, умножение на постоянную и переход к пределу можно менять местами.

        Следствие 2.5   Пусть функции  имеют при базе  пределы, равные соответственно , и -- постоянные. Тогда

        Доказательство.     Оно состоит в последовательном -кратном применении теоремы 2.8 к слагаемым , предел которых, согласно предыдущему следствию, равен . 

В качестве частного случая можно рассмотреть предел разности двух функций. Разность  можно представить в виде  и применить следствие 2.5 к этой сумме из двух слагаемых. Получим тогда, что

то есть что разность (как и сумма) сохраняется при переходе к пределу.

        Замечание 2.4   Утверждение следствия 2.5, с алгебраической точки зрения, означает, что, во-первых, множество  всех функций, заданных на фиксированном окончании  базы  и имеющих предел при базе -- это линейное пространство, а во-вторых -- что операция взятия предела -- это линейное отображение линейного пространства  в линейное пространство вещественных чисел . Попросту: переход к пределу сохраняет суммирование и умножение на постоянные.

Предел отношения двух функций , в отличие от суммы, разности и произведения, не обязательно равен отношению пределов числителя  и знаменателя , даже если пределы  и  существуют. Дело в том, что предел знаменателя может равняться нулю, и отношение пределов тогда не имеет смысла, в то время как предел отношения  при этом вполне может существовать. Приведём такой простейший пример:

        Пример 2.15   Пусть ,  и взята база . Тогда, очевидно, ,  и отношение пределов  не имеет смысла. При этом  при  и предел отношения существует: .

Оказывается, условия , которое обеспечивает то, что отношение пределов имеет смысл, -- этого условия достаточно для того, чтобы предел отношения двух функций был равен отношению их пределов. Ниже мы докажем соответствующую теорему, а пока докажем такое вспомогательное утверждение.

        Лемма 2.1   Пусть при некоторой базе  существует предел . Тогда функция  определена на некотором окончании этой базы и локально ограничена при этой базе.

        Доказательство.     Возьмём положительное число . По определению предела, в базе  найдётся такое окончание , что при всех  будет . Это неравенство можно привести к виду

(2.2)

При  это неравенство означает, что ; так как , то и  при всех  и, следовательно, функция  определена во всех точках окончания  и удовлетворяет неравенству

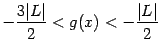При  неравенство (2.2) означает, что ; так как 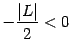, то и  при всех  и, опять-таки, функция  определена во всех точках окончания ; она удовлетворяет неравенству

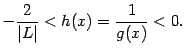
В любом случае получаем, что функция  определена во всех точках  и при этих  удовлетворяет неравенству , что означает локальную ограниченность функции при базе .      

На основе этой леммы мы докажем обещанное выше утверждение о пределе отношения.

        Теорема 2.10   Пусть при одной и той же базе  существуют пределы  и , причём . Тогда функция  определена на некотором окончании базы , существует предел , и , то есть предел отношения равен отношению пределов числителя и знаменателя.

        Доказательство.     Представим отношение  в виде 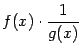, в котором и первый, и второй множители определены на некотором окончании  базы  (относительно второго множителя см. предыдущую лемму). Поэтому и исходное отношение имеет смысл при всех .

Утверждение о том, что 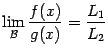, эквивалентно тому, что разность -- бесконечно малая величина. Приводя эту разность к общему знаменателю, получим, что . Величина -- постоянная и, следовательно (см.пример 2.11), локально ограничена; функция -- тоже локально ограничена при базе  (по предыдущей лемме). Значит, с учётом предложения 2.1 и теоремы 2.7, будет доказано, что величина  бесконечно малая, если мы покажем, что бесконечно мала при базе  величина . Найдём предел этой величины. По свойству линейности предела ( следствие 2.5)

Это означает, что величина  бесконечно мала.      

        Замечание 2.5   Как и в случае пределов суммы и произведения, можно сделать замечание (аналогичное замечаниям 2.2 и 2.3): если существует предел отношения, то пределы числителя и знаменателя, вообще говоря, существовать не обязаны. Приведите сами пример, иллюстрирующий это утверждение.     

        Пример 2.16   Найдём предел

Разделим числитель и знаменатель дроби на старшую степень , то есть на , и получим предел

В этом пределе знаменатель стремится к 3, так как  и  (здесь мы применили теорему о пределе произведения для последнего слагаемого) и, следовательно,  (здесь мы воспользовались линейностью предела). Поскольку предел знаменателя оказался не равен 0, то можно применить теорему о пределе отношения и получить, что

Предел числителя, равный 2, мы нашли аналогично пределу знаменателя, пользуясь линейностью предела.

Итак,

    

Заметим, что предел отношения многочленов оказался равен отношению коэффициентов при старшей степени , то есть, в данном случае, при .

Аналогично решаются и другие примеры на вычисление пределов отношения двух многочленов при , а также пределов отношения некоторых других функций, например, связанных с корнями из многочленов.

        Пример 2.17   Найдём предел

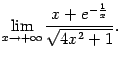
Для этого поделим числитель и знаменатель дроби на  (под знаком корня в знаменателе для этого придётся поделить на ):

Поскольку , то подкоренное выражение стремится к 4, а весь знаменатель -- к .⁶ Предел знаменателя оказался отличен от 0, поэтому предел отношения равен отношению пределов. Найдём предел числителя. Поскольку  при всех  (так как показатель степени отрицателен), то величина  локально ограничена при базе  и поскольку величина -- бесконечно малая при этой базе, то произведение  также бесконечно мало, то есть стремится к 0 при . Значит, предел числителя равен

а исходный предел --

    

        Упражнение 2.5   Найдите пределы:

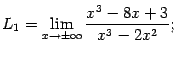
Ответ: ; ; .

Указания: поделите числитель и знаменатель дроби в первом примере на , во втором -- на  и в третьем -- на . Во втором примере воспользуйтесь тем, что  и -- величины, ограниченные при всех  (и, следовательно, локально ограниченные при любой базе).     

        Теорема 2.11 (теорема "о двух милиционерах")   Пусть даны три функции ,  и , при всех  из некоторого окончания  базы  связанные неравенством

Пусть функции  и  имеют общий предел при базе :

Тогда функция  также имеет предел при базе , равный тому же числу :

        Доказательство.     Согласно определению предела, для любого  найдутся такие окончания базы  и , что при  выполняется неравенство

а при  -- неравенство

Значит, для окончания  при всех  выполняются неравенства

то есть

Это означает, что предел величины  равен .      

Рис.2.21.Два милиционера  и  и пьяный  движутся в участок 

(Происхождение названия теоремы таково: пусть график функции -- это траектория движения первого милиционера в участок, график -- второго милиционера туда же, а график -- траектория движения нетрезвого гражданина, находящегося, в соответствии с неравенством

в любой момент  между двумя милиционерами. Тогда и этот гражданин неизбежно придёт туда же, в участок .)

        Теорема 2.12 (теорема о пределе неотрицательной величины)   Пусть  при всех  из некоторого окончания  базы  и существует . Тогда . Иными словами, при переходе к пределу знак нестрогого неравенства сохраняется.

        Доказательство.     Если бы предел  был отрицательным, то можно было бы взять  и найти такое окончание базы , что при  выполняется неравенство, откуда . Это же будет выполнено на некотором окончании , что противоречит предположению, что  при всех . Противоречие доказывает, что отрицательным предел  быть не может, то есть . 

        Следствие 2.6   Пусть  при всех  из некоторого окончания  базы  и существует . Тогда .

        Доказательство.     Для доказательства достаточно взять функцию , применить к ней доказанную только что теорему и воспользоваться тем, что знак минус можно вынести за знак предела (по свойству линейности предела). 

        Следствие 2.7 (переход к пределу в нестрогом неравенстве)   Пусть при всех  из некоторого окончания  базы  выполняется неравенство . Предположим, что существуют пределы  и . Тогда  (то есть значения пределов связаны тем же нестрогим неравенством, что и функции). То же верно для нестрогого неравенства .

        Доказательство.     Рассмотрим функцию . По условию теоремы, , причём

Применим к функции  теорему о пределе неотрицательной величины и получим, что , то есть , что и требовалось доказать. Для другого нестрогого неравенства доказательство аналогично.      

        Замечание 2.6   Аналогичные утверждения для строгих неравенств ( и ) неверны. Для того, чтобы в этом убедиться, достаточно рассмотреть предел . Очевидно, он равен 0, хотя при любом  из любого окончания  базы  величина  строго положительна.    

Рис.2.22.Предел строго положительной величины может оказаться равным 0

Напомним, что функция  называется не убывающей на множестве , если для любых , таких что , выполняется неравенство , и не возрастающейна , если при  и  выполняется неравенство .

        Теорема 2.13 (о пределе монотонной функции)   Пусть рассматривается одна из баз , , , которую обозначим . Пусть функция  не убывает на некотором окончании  базы  и ограничена сверху на этом окончании, то есть существует такая постоянная , что  при всех . Тогда существует предел , причём .

Рис.2.23.Предел неубывающей ограниченной сверху функции

Доказательство этой теоремы достаточно сложно; оно основывается на довольно тонких свойствах системы вещественных чисел, а именно, на том, что у ограниченного снизу множества чисел , где числа  ограничивают функцию  сверху, существует точная нижняя грань ; она-то и будет пределом неубывающей функции.

Мы ограничимся здесь этим замечанием и поясняющим рисунком, а за подробным доказательством отошлём читателя к полному курсу математического анализа, например, книгам:Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. 1 или С. М. Никольский, Курс математического анализа, т. 1.    

Имеют место также утверждения, получающиеся из теоремы о пределе монотонной функции сменой знака функции или заменой координаты :

        Следствие 2.8   Пусть рассматривается одна из баз , , , которую обозначим . Пусть функция  не возрастает на некотором окончании  базы   и ограничена снизу на этом окончании, то есть существует такая постоянная , что  при всех . Тогда существует предел , причём .

Рис.2.24.Предел невозрастающей ограниченной снизу функции

        Следствие 2.9   Пусть рассматривается одна из баз , , которую обозначим . Пусть функция  не убывает на некотором окончании  базы  и ограничена снизу на этом окончании, то есть существует такая постоянная , что  при всех . Тогда существует предел , причём .

Рис.2.25.Предел неубывающей ограниченной снизу функции

        Следствие 2.10   Пусть рассматривается одна из баз , , которую обозначим . Пусть функция  не возрастает на некотором окончании  базы   и ограничена сверху на этом окончании, то есть существует такая постоянная , что  при всех . Тогда существует предел , причём .

Рис.2.26.Предел невозрастающей ограниченной сверху функции