8 Формулировка

Для всякой системы вложенных отрезков

существует хотя бы одна точка c, принадлежащая всем отрезкам данной системы.

Если, кроме того, длина отрезков системы стремится к нулю:

то c — единственная общая точка всех отрезков данной системы.

Доказательство

1) Существование общей точки. Множество левых концов отрезков {a_n} лежит на числовой прямой левее множества правых концов отрезков {b_n}, поскольку

В силу аксиомы непрерывности, существует точка c, разделяющая эти два множества, то есть

в частности

Последнее неравенство означает, что c — общая точка всех отрезков данной системы.

2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки c и c', принадлежащие всем отрезкам системы:

Тогда для всех номеров n выполняются неравенства:

В силу условия стремления к нулю длин отрезков для любого  для всех номеров n, начиная с некоторого будет выполняться неравенство

b_n − a_n < ε

Взяв в этом неравенстве , получим

Противоречие. Лемма доказана полностью.

9 Подпоследовательность. Частичные пределы последовательности.

Определение (определение подпоследовательности). Как мы уже знаем (см. определение последовательности) последовательность это функция, заданная на множестве натуральных чисел. Если вместо множества всех натуральных чисел взять некоторое его бесконечное подмножество n_k, k = 1,2,..., n_k<n_k+1, то получим подпоследовательность x_nk.

Пример 27.

x_n = {n}=1,2,3,...,n,... x_nk = {1,3,...,2n-1,...}

Определение 35 (определение частичного предела). Предел  любой подпоследовательности, если он существует, называется частичным пределом данной последовательности.

Определение 36. Частичный предел последовательности называется предельной точкой данной последовательности.

Иначе говоря справедливо следующее определение предельной точки последовательности.

Определение 37 (определение предельной точки). Точка

a R называется предельной точкой последовательности x_n, если в любой  – окрестности этой точки содержится бесконечно много элементов последовательности x_n.

Замечание. Если последовательность сходится, то по теореме 7, она имеет единственную предельную точку. Если

x_n не является сходящейся, то она может иметь несколько предельных точек (и, вообще бесконечно много предельных точек).

Пример 28. Рассмотрим последовательность

x_n = (-1)ⁿ. Так как x_2k = 1, x_2k+1 = -1, то данная последовательность имеет два частичных предела, или иначе говоря, две предельные точки. Если последовательность ограничена сверху, то множество всех частичных пределов тоже ограничено сверху. Можно доказать, что это множество обязательно содержит максимальный элемент. Этот максимальный элемент называется верхним пределом последовательности и обозначается lim_nx_n.

Если последовательность не ограничена сверху, то

lim_nx_n = +.

Аналогично определяется lim_nx_n – нижний предел последовательности. Если последовательность не ограничена снизу, то

lim_nx_n = -.

Определение 38. Нижним пределом последовательности называется наименьший частичный предел последовательности.

Верхним пределом последовательности называется наибольший частичный предел последовательности.

Условие существования предела последовательности эквивалентно условию равенства верхнего и нижнего пределов этой последовательности.

Вычисление верхнего и нижнего пределов последовательности сводится к тому, что выделяют сходящиеся подпоследовательности и сравнивают их пределы.

Пример 29. Пусть дана последовательность x_n = n^(-1)n, n N. Так как x_2k = 2k, x_2k+1 = 1/(2k+1), то lim_nx_n = +. и lim_nx_n = 0.

Теорема 13 (теорема Больцано-Вейерштрасса). Из всякой ограниченной последовательности действительных чисел, можно выделить сходящуюся подпоследовательность.

10

Теорема 7. Числовая последовательность может иметь только один предел.

Доказательство. Предположим противное. Это означает, что существует последовательность , имеющая два различных предела а и в. По лемме  и , где  и  – бесконечно малые последовательности, откуда получаем . Так как все элементы бесконечно малой последовательности  имеют одно и по же значение в-а, то в-а=0, то есть в=а, что противоречит предположению. Теорема доказана.

Теорема 8. Сходящаяся числовая последовательность ограничена.

Доказательство. Пусть  – сходящаяся к числу а, тогда , где . Так как бесконечно малая последовательность ограничена, то $ такое число , что для всех  выполняется. Поэтому  для всех , а это и означает, что последовательность  ограничена.

Теорема 9. Если последовательность  сходится к числу а, то и любая подпоследовательность этой последовательности сходится к этому же числу.

Доказательство. По условию , то есть для любого числа  существует такой номер N, что для всех номеров  выполняется неравенство . Пусть  – некоторая подпоследовательность последовательности . Тогда для всех номеров  выполняется , поэтому .

Замечание. Теорема 3 справедлива для случая , то есть для бесконечно большой последовательности . Таким образом, каждая подпоследовательность бесконечно большой последовательности является бесконечно большой последовательностью. Доказательство этого утверждения аналогично доказательству теоремы 3.

Теорема 10. Если последовательность  сходится к числу , то, начиная с некоторого номера, определена последовательность , которая является ограниченной.

Доказательство. Пусть , так как . Пусть N – номер, начиная с которого выполняется условие . Отсюда при  получаем  или . Тогда при  , что означает ограниченность последовательности , начиная с номера N.

Рассмотрим теперь несколько простейших свойств пределов числовых последовательностей.

1. Если , , с – действительное число, то .

Доказательство. Последовательность  – бесконечно малая и поэтому по лемме .

2. Если последовательность сходится, то последовательности  также сходятся, причем .

Доказательство. Пусть , . По лемме , , , где . Следовательно, , где по свойству бесконечно малых последовательностей . Поэтому по лемме получаем .

Следствие. Свойство 2 выполняется для любого конечного числа сходящихся последовательностей.

3. Если последовательности  и  сходятся, то последовательность  также сходится, причем .

Доказательство. Пусть , , тогда , , , где , поэтому . По свойствам бесконечно малых последовательностей  – бесконечно малая. Тогда по лемме .

Следствие 1. Если последовательность  сходится, то для любого числа с последовательность  также сходится, причем .

Следствие 2. Если последовательность  сходится и k – натуральное число, то последовательность {} также сходится, причем .

4. Если последовательности  и  сходятся,  при  и , то последовательность  также сходится, причем .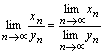

Доказательство. Пусть , , тогда , , где . По теореме 10 существует номер N такой, что для всех номеров  последовательность  ограничена

 

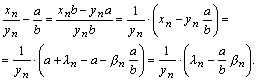
Последовательность  бесконечно малая при , так как  – ограничена, а  – бесконечно малая последовательность. Таким образом, теорема доказана.