11 Теорема Больцано-Вейерштрасса

Пусть задана произвольная последовательность действительных чисел  . Выберем из нее бесконечное множество элементов с номерами . Тогда получим новую последовательность , которая называется подпоследовательностью последовательности . Таких подпоследовательностей можно выделить из данной последовательности бесконечное множество.

Если последовательность сходится (к конечному числу, или ), то очевидно, что и любая ее подпоследовательность тоже сходится и притом к тому же числу (конечному, или).

Последовательность

(1)

может служить примером не сходящейся последовательности чисел. Все же мы видим, что эта последовательность содержит в себе подпоследовательность 

,

сходящуюся (к 1). Возникает вопрос, всегда ли это так, всякая ли последовательность действительных чисел содержит в себе подпоследовательность, сходящуюся к некоторому числу (конечному, , ). Положительный ответ на этот вопрос дает

Т е о р е м а  1. Из всякой последовательности действительных чисел можно выделить подпоследовательность, сходящуюся к конечному числу, или к , или к .

В случае, когда последовательность не ограничена сверху (снизу), она, очевидно, содержит в себе подпоследовательность, стремящуюся к (к ), что доказывает теорему. Если же последовательность ограничена, то теорема 1 сводится к следующей теореме.

Т е о р е м а  2 (Больцано-Вейерштрасса). Из всякой ограниченной последовательности можно выделить подпоследовательность , сходящуюся к некоторому числу.

Д о к а з а т е л ь с т в о. Так как последовательность точек ограничена, то все они принадлежат к некоторому отрезку , который обозначим через . Разделим на два равных отрезка и обозначим через самый правый из  них, содержащий в себе бесконечное число элементов . Один из этих элементов обозначим через . Правее , если есть, то конечное число точек . Разделим на два равных отрезка и обозначим через самый правый из них, содержащий в себе бесконечное число элементов . Выберем среди этих элементов одинс номером . Правее , если есть точки , то их конечное число.

Продолжим этот процесс по индукции. В результате получим последовательность вложенных друг в друга отрезков , длины которых , , и  подпоследовательность точек нашей последовательности таких, что . При этом правее каждого из отрезков имеется не более чем конечное число элементов .

На основании принципа вложенных отрезков существует точка , принадлежащая к любому из отрезков . Очевидно, что подпоследовательность имеет своим пределом , и мы доказали теорему.

12

Определение 32 (последовательность Коши). Последователь ность x_n называется фундаментальной или последовательностью Коши, если  > 0 N:  n>N,  p-натурального, |x_n+p-x_n| < 

Теорема 11 (Критерий Коши). Числовая последовательность сходится тогда и только тогда, когда она является фундаментальной.

Пример 24. Используя критерий Коши можно доказать, что последовательность (-1)ⁿ не имеет предела . Очевидно, что |x_n-x_n+1| = 2, поэтому если выбрать  = 1, то получим отрицание утверждения, что последовательность фундаментальна. А именно:

>0,  n>N,  m>N, |x_n-x_m|.

Пример 25. Рассмотрим последовательность

x_n = 1+1/2+1/3+....+1/n Для исследования на сходимость воспользуемсяопределением фундаментальности Так как |x_n+p - x_n| = 1/(n+1)+ ... + 1/(n+p) >p/(n+p) , то при p=n |x_n+p - x_n|>n/2n = 1/2 = . Очевидно, что определениефундаментальной последовательности не выполняется. В силу критерия Коши эта последовательность не имеет предела.

13

 

Фу́нкция отношение двух (группы) объектов, в котором изменение одного из них ведёт к изменению другого. Ф. может рассматриваться с точки зрения следствий (благоприятных, неблагоприятных — дисфункциональных или нейтральных — афункциональных), вызываемых изменением одного параметра в др. параметрах объекта (функциональность), или взаимосвязи отдельных частей в рамках некоторого целого (функционирование).

Предел функции по Гейне

Значение  называется пределом (предельным значением) функции  в точке , если для любой последовательности точек , сходящейся к , но не содержащей  в качестве одного из своих элементов (то есть в проколотой окрестности  ), последовательность значений функции  сходится к .^[1]

Предел функции по Коши

Значение  называется пределом (предельным значением) функции  в точке , если для любого наперёд взятого положительного числа ε найдётся отвечающее ему положительное число  такое, что для всех аргументов , удовлетворяющих условию , выполняется неравенство .^[1]

Окрестностное определение по Коши

Значение  называется пределом (предельным значением) функции  в точке , если для любой окрестности  точки  существует выколотая окрестность  точки такая, что образ этой окрестности  лежит в . Фундаментальное обоснование данного определения предела можно найти в статье Предел вдоль фильтра.

Эквивалентность определений

Все данные выше определения предела функции в точке эквивалентны.^[1] Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.

14

Критерий Коши о существовании предела функции.

Определение 10 (условие Коши). Будем говорить, что функция f(x) удовлетворяет в точке a условию Коши, если для любого положительного числа найдется положительное (), что для любых x₁,x₂, удовлетворяющих условию

0<|x1-a|<, 0<|x2-a|<,

справедливо неравенство

|f(x1-f(x2)|<.

Теорема 5 (Критерий Коши). . Для того, чтобы существовал предел функции f(x) в точке a ( lim_x  af(x) = A ) необходимо и достаточно, чтобы f(x) удовлетворяла в точке a условию Коши.

Аналогично формулируется условие Коши и доказывается критерий Коши и для случаев правого(левого) пределов в точке a, предела при x().

15

Определения

Пусть на некотором числовом множестве  задана числовая функция  и число  — предельная точка области определения . Существуют различные определения для односторонних пределов функции  в точке , но все они эквивалентны.

Односторонний предел по Гейне

• Число  называется правосторонним пределом (правым пределом, пределом справа) функции  в точке , если для всякой последовательности , состоящей из точек, больших числа , которая сама сходится к числу , соответствующая последовательность значений функции  сходится к числу .

• Число 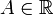 называется левосторонним пределом (левым пределом, пределом слева) функции  в точке , если для всякой последовательности 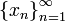, состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции  сходится к числу .^[1]