
- •Система аксиом действительных чисел Аксиомы сложения
- •Аксиомы умножения
- •Аксиомы порядка
- •Верхняя и нижняя грани числовых множеств
- •Определение предела числовой последовательности
- •Единственность предела
- •Теорема об ограниченности сходящейся последовательности
- •Предел постоянной величины
- •Предельный переход в неравенствах
- •3 Бесконечно малые и бесконечно большие последовательности и их свойства.
- •6 Монотонные последовательности
- •Теорема Больцано – Вейерштрасса
- •Второй замечательный предел
- •8 Формулировка
- •Доказательство
- •9 Подпоследовательность. Частичные пределы последовательности.
- •11 Теорема Больцано-Вейерштрасса
- •Односторонний предел по Коши
- •19 Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
6 Монотонные последовательности
Определение. Последовательность {xn} называется возрастающей, если для всех номеров n имеем xn < xn+1; неубывающей, если для всех номеров n имеемxn ≤ xn+1; убывающей, если для всех номеров n имеем xn > xn+1; невозрастающей, для всех номеров n имеем xn ≥ xn+1.
Теорема Больцано – Вейерштрасса
Монотонно
возрастающая (убывающая) ограниченная
сверху (снизу) последовательность должна
иметь предел.
Действительно.
В этом случае для возрастающей
последовательности должна существовать
такая точка ξ , для которой а) справа нет
ни одной точки последовательности, б)
слева от неё в любой как угодно малой
окрестности существует бесконечно
много членов последовательности. Если
справа от точки ξ попалась хотя бы одна
точка последовательности, то из-за
возрастания последовательности справа
от точки ξ будет бесконечно много членов
числовой последовательности. Тогда это
должна быть другая точка η > ξ и так
далее. Если всё - таки такой точки не
будет, то это приведёт к противоречию
с требованием ограниченности
последовательности. Так как в сколь
угодно малой окрестности точки ξ (хотя
бы слева) есть бесконечное число точек
последовательности, то эта точка ξ
является пределом этой последовательности.
Если слева было бы конечное число точек
последовательности и бесконечно справа,
то это была бы другая точка ξ, что приводит
опять к противоречию об ограниченности
последовательности.
Существует
другая формулировка теоремы Больцано
– Вейерштрасса. Из
любой ограниченной последовательности
можно выделить сходящуюся
подпоследовательность.
Доказательство.
Пусть последовательность ограничена,
то есть существует такой отрезок [а, b],
что хn![]() [а, b]
[а, b] ![]() n =
1, 2, 3, … Разделим отрезок [а, b]
пополам, и по крайней мере один из
получившихся отрезков содержит бесконечно
много элементов данной последовательности.
Пусть это будет отрезок [а1, b1],
и так далее. Получим систему вложенных
отрезков (см.
ниже)
[a, b]
n =
1, 2, 3, … Разделим отрезок [а, b]
пополам, и по крайней мере один из
получившихся отрезков содержит бесконечно
много элементов данной последовательности.
Пусть это будет отрезок [а1, b1],
и так далее. Получим систему вложенных
отрезков (см.
ниже)
[a, b] ![]() [a1,b1]
[a1,b1] ![]() [a2,b2]
[a2,b2]![]() …
… ![]() [an,bn]
[an,bn] ![]() …
Выберем по одному элементу последовательности
из каждого отрезка
…
Выберем по одному элементу последовательности
из каждого отрезка
![]()
Последовательность {xnk} является подпоследовательностью последовательности {xn}. Так как
![]()
то
существует такая точка ξ ![]() [а,
b], что
[а,
b], что
![]()
Так как an ≤ xn ≤ bn, то
![]()
7
Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
Второй замечательный предел
![]() или
или ![]()
Доказательство второго замечательного предела:
Доказательство для натуральных значений x
![]() Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что ![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1.
Пусть ![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами: ![]() ,
где
,
где ![]() —
это целая часть x.
—
это целая часть x.
Отсюда
следует: ![]() ,
поэтому
,
поэтому
 .
.
Если ![]() ,
то
,
то ![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу ![]() ,
имеем:
,
имеем:

![]() .
.
По
признаку (о пределе промежуточной
функции) существования пределов ![]() .
.
2.
Пусть ![]() .
Сделаем подстановку − x = t,
тогда
.
Сделаем подстановку − x = t,
тогда
![]()
![]() .
.
Из
двух этих случаев вытекает, что ![]() для
вещественного x.
для
вещественного x.
Следствия



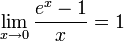
 для
для  ,
, 

