
вышмат полезно
.pdf
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Государственное образовательное учреждение высшего профессионального образования
Московский технический университет связи и информатики Кафедра математического анализа
Р.В. Арутюнян, И.А.Гудкова, А.В.Куприн, А.Р. Лакерник, А.М. Райцин
ПРАКТИКУМ ПО ВЫСШЕЙ МАТЕМАТИКЕ ДЛЯ БАКАЛАВРОВ ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Москва 2016
План УМД 2015/2016 уч. г.
ПРАКТИКУМ ПО ВЫСШЕЙ МАТЕМАТИКЕ ДЛЯ БАКАЛАВРОВ ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Авторы: Р.В. Арутюнян, канд. физ-мат наук, доцент И.А.Гудкова, ст. преподаватель А.В.Куприн, доцент А.Р. Лакерник, канд. физ-мат наук, доцент
А.М. Райцин, доктор тех. наук, профессор
Издание утверждено методическим советом ОТФ. Протокол № от 27.03.2016г.
Ответственный редактор: Арутюнян Р.В.
Рецензент: Зайцев А.А. , доцент кафедры ВТ и АОАИ МИИГАиК Рецензент: Данилов В.Г., доктор физ. мат. наук, профессор МТУСИ
Введение
Предлагаемое учебное пособие «Практикум по высшей математике для бакалавров Дифференциальное и интегральное исчисление» направлен на получение практических навыков по математике в соответствии с первым семестром рабочей программы по направлению «Инфокоммуникационные технологии и системы связи». Каждый раздел практикума содержит опорный конспект, отражающий в сжатой форме основные теоретические сведения изучаемой темы, необходимые для практического применения материала. В каждый раздел включены типовые задачи для аудиторных занятий с решениями и задачи для самостоятельной работы. Структура практикума такова, что каждому его разделу соответствует тема рабочей программы, что представляется полезным, так как позволяет самостоятельно изучать материал, в случае пропуска студентом аудиторногозанятия и,чтоотличает, дано пособие от существующих. Кроме того, практикум позволяет при уменьшении числа аудиторных часов по программе для бакалавров уделять большее внимание самостоятельной работе, разбирая типовые решения и выполняя предлагаемые задания. Задачи, предлагаемые к решению взяты из Бермана Г.Н. Сборник задач по курсу математического анализа. 20-е изд.;
М.: Наука,1985. 384с.
3
СОДЕРЖАНИЕ |
|
Введение............................................................................................................... |
3 |
ЗАНЯТИЕ 1 |
|
1. ФУНКЦИЯ И СПОСОБЫ ЕЕ ЗАДАНИЯ.................................................... |
8 |
1.1.Функция.......................................................................................................... |
8 |
1.2. Основные способы задания функции........................................................ |
9 |
1.3. Графики элементарных функций ............................................................. |
10 |
1.4. Основные приемы построения графиков функций ................................ |
12 |
1.5. Бесконечные числовые последовательности .......................................... |
13 |
1.6. Решение некоторых типовых задач, рассматриваемых в аудитории... |
14 |
1.7. Задачи для самостоятельного решения.................................................... |
18 |
ЗАНЯТИЕ 2 |
|
2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ФУНКЦИИ............... |
19 |
2.1. Предел последовательности...................................................................... |
19 |
2.2. Предел функции......................................................................................... |
20 |
2.3. Решение некоторых типовых задач, рассматриваемых в аудитории... |
23 |
2.4. Задачи для самостоятельного решения.................................................... |
26 |
ЗАНЯТИЕ 3. |
|
3. ВЫЧИСЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ .................................................. |
27 |
3.1. Решение некоторых типовых задач, рассматриваемых в аудитории... |
27 |
3.2. Задачи для самостоятельного решения.................................................... |
30 |
ЗАНЯТИЕ 4. |
|
4. СРАВНЕНИЕ ПЕРЕМЕННЫХ ВЕЛИЧИН ............................................... |
31 |
4.1. Бесконечно малые функции и их сравнение........................................... |
31 |
4.2. Решение некоторых типовых задач, рассматриваемых в аудитории... |
34 |
4.3. Задачи для самостоятельного решения.................................................... |
35 |
ЗАНЯТИЕ 5. |
|
5. НЕПРЕРЫВНОСТЬ ФУНКЦИИ................................................................ |
36 |
5.1. Непрерывность функции в точке.............................................................. |
36 |
5.2. Основные теоремы о непрерывных функциях........................................ |
37 |
5.3. Непрерывность и разрывы монотонной функции. Свойства функций, |
|
непрерывных на отрезке............................................................................ |
38 |
5.4. Решение некоторых типовых задач, рассматриваемых в аудитории... |
40 |
5.5. Задачи для самостоятельного решения.................................................... |
43 |
ЗАНЯТИЕ 6. |
|
6. ТОЧКИ РАЗРЫВА........................................................................................ |
44 |
6.1. Точки разрыва и их классификация......................................................... |
44 |
6.2. Решение некоторых типовых задач, рассматриваемых в аудитории... |
44 |
6.3. Задачи для самостоятельного решения.................................................... |
50 |
ЗАНЯТИЕ 7. |
|
7. ПРОИЗВОДНЫЕ ПЕРВОГО ПОРЯДКА ................................................... |
50 |
7.1. Вычисление производных. Производная сложной функции................. |
50 |
4 |
|
7.2. Решение некоторых типовых задач, рассматриваемых в аудитории... |
53 |
7.3. Задачи для самостоятельного решения.................................................... |
57 |
ЗАНЯТИЕ 8. |
|
8. ПРОИЗВОДНЫЕ ПЕРВОГО ПОРЯДКА ................................................... |
58 |
8.1. Логарифмическое дифференцирование и производная неявной |
|
функции....................................................................................................... |
58 |
8.2. Решение некоторых типовых задач, рассматриваемых в аудитории... |
58 |
8.3. Задачи для самостоятельного решения.................................................... |
60 |
ЗАНЯТИЕ 9. |
|
9. ПРОИЗВОДНЫЕ ПЕРВОГО ПОРЯДКА ................................................... |
61 |
9.1. Производная параметрически заданной функции. Приложения |
|
производной................................................................................................ |
61 |
9.2. Решение некоторых типовых задач, рассматриваемых в аудитории... |
62 |
9.3. Задачи для самостоятельного решения.................................................... |
65 |
ЗАНЯТИЕ 10. |
|
10. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ .... |
65 |
10.1. Дифференциал функции. Приложение к приближенным |
|
вычислениям............................................................................................... |
65 |
10.2. Производные и дифференциалы высших порядков. Формула |
|
Лейбница................................................................................................... |
67 |
10.3. Основные теоремы дифференциального исчисления.......................... |
69 |
10.4. Решение некоторых типовых задач, рассматриваемых в аудитории.71
10.5. Задачи для самостоятельного решения.................................................. |
74 |
ЗАНЯТИЕ 11. |
|
11. ТЕСТ И КОНТРОЛЬНАЯ РАБОТА.......................................................... |
75 |
ЗАНЯТИЕ 12 |
|
12. ПРАВИЛО ЛОПИТАЛЯ............................................................................. |
75 |
12.1. Формулировка теоремы........................................................................... |
75 |
12.2. Решение некоторых типовых задач, рассматриваемых в аудитории.75
12.3. Задачи для самостоятельного решения.................................................. |
77 |
ЗАНЯТИЕ 13 |
|
13. ПРАВИЛО ЛОПИТАЛЯ (продолжение).................................................. |
77 |
13.1. Решение некоторых типовых задач, рассматриваемых в аудитории.78
13.2. Задачи для самостоятельного решения.................................................. |
79 |
ЗАНЯТИЕ 14 |
|
14. ФОРМУЛА ТЕЙЛОРА............................................................................... |
79 |
14.1. Формулировка теоремы........................................................................... |
79 |
14.2. Решение некоторых типовых задач, рассматриваемых в аудитории.81
14.3. Задачи для самостоятельного решения.................................................. |
83 |
ЗАНЯТИЕ 15 |
|
15. ФОРМУЛА ТЕЙЛОРА (продолжение) .................................................... |
85 |
15.1. Решение некоторых типовых задач, рассматриваемых в аудитории.85
15.2. Задачи для самостоятельного решения.................................................. |
86 |
ЗАНЯТИЕ 16
5
16. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ. ЭКСТРЕМУМ.............. |
87 |
16.1. Определения и формулировки теорем................................................... |
87 |
16.2. Решение некоторых типовых задач, рассматриваемых в аудитории.88
16.3. Задачи для самостоятельного решения.................................................. |
91 |
ЗАНЯТИЕ 17 |
|
17. ИССЛЕДОВАНИЕ И ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ............. |
91 |
17.1. Определения и формулировки теорем................................................... |
91 |
17.2. Решение некоторых типовых задач, рассматриваемых в аудитории.93
17.3. Задачи для самостоятельного решения.................................................. |
96 |
ЗАНЯТИЕ 18
18. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ.................................................................... |
97 |
18.1. Основные понятия. Предел. Непрерывность. Частные производные 97
18.2. Частные производные.............................................................................. |
98 |
18.3. Решение некоторых типовых задач, рассматриваемых в аудитории.99
18.4. Задачи для самостоятельного решения................................................ |
100 |
ЗАНЯТИЕ 19 |
|
19. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ................................................. |
101 |
19.1. Понятие полного дифференциала ........................................................ |
101 |
19.2. Формула Тейлора................................................................................... |
102 |
19.3. Решение некоторых типовых задач, рассматриваемых в аудитории102
19.4. Задачи для самостоятельного решения................................................ |
104 |
ЗАНЯТИЕ 20 |
|
20. ПРОИЗВОДНЫЕ СЛОЖНОЙ И НЕЯВНОЙ ФУНКЦИИ. |
|
ЭКСТРЕМУМЫ. ....................................................................................... |
105 |
20.1. Сложные функции и их дифференцирование..................................... |
105 |
20.2. Неявные функции и их дифференцирование...................................... |
105 |
20.3. Решение некоторых типовых задач, рассматриваемых в аудитории106
20.4. Задачи для самостоятельного решения................................................ |
107 |
20.5. Локальные экстремумы функции двух переменных.......................... |
108 |
20.6. Условный экстремум функции двух переменных.............................. |
108 |
20.7. Решение некоторых типовых задач, рассматриваемых в аудитории109
20.8. Задачи для самостоятельного решения................................................ |
111 |
ЗАНЯТИЕ 21 |
|
21. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ФМП .. |
111 |
21.1. Производная в данном направлении и градиент ................................ |
111 |
21.2. Касательная прямая и нормальная плоскость к кривой в простран - |
|
стве........................................................................................................... |
112 |
21.3. Касательная плоскость и нормаль к поверхности.............................. |
112 |
21.4. Применение дифференциалов к приближенным вычислениям........ |
112 |
21.5. Решение некоторых типовых задач, рассматриваемых в аудитории113
21.6. Задачи для самостоятельного решения................................................ |
115 |
ЗАНЯТИЕ 22
22. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ТАБЛИЧНОЕ ИНТЕГРИРО –
6
ВАНИЕ....................................................................................................... |
116 |
22.1. Первообразная и неопределенный интеграл....................................... |
116 |
22.2. Свойства неопределенного интеграла ................................................. |
116 |
22.3. Таблица интегралов ............................................................................... |
117 |
22.4. Решение некоторых типовых задач, рассматриваемых в аудитории119
22.5. Задачи для самостоятельного решения................................................ |
121 |
ЗАНЯТИЕ 23
23. ВНЕСЕНИЕ ПОД ЗНАК ДИФФЕРЕНЦИАЛА. ИНТЕГРИРОВАНИЕ
МЕТОДОМ ПОДСТАНОВКИ................................................................. |
122 |
23.1. Внесение под знак дифференциала...................................................... |
122 |
23.2. Решение некоторых типовых примеров на внесение под знак |
|
дифференциала....................................................................................... |
122 |
23.3. Интегрирование методом подстановки ............................................... |
124 |
23.4. Решение некоторых типовых примеров на метод подстановки........ |
125 |
23.5. Задачи для самостоятельного решения................................................ |
127 |
ЗАНЯТИЕ 24 |
|
24. МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ........................................ |
128 |
24.1. Описание метода интегрирования по частям...................................... |
128 |
24.2. Рекуррентная формула для интеграла |
|
|
dx |
128........................... |
|
(x2 |
a2)n 1 |
||||
|
|
||||
24.3. Решение некоторых типовых задач, рассматриваемых в аудитории129
24.4. Задачи для самостоятельного решения................................................ |
131 |
ЗАНЯТИЕ 25 |
|
25. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ ....................... |
132 |
25.1. Элементарные дроби и их интегралы.................................................. |
132 |
25.2. Разложение правильной дроби в сумму элементарных дробей........ |
133 |
25.3. Решение некоторых типовых задач, рассматриваемых в аудитории135
25.4. Задачи для самостоятельного решения................................................ |
138 |
ЗАНЯТИЕ 26 |
|
26. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ .................. |
138 |
26.1. Интегрирование иррациональностей от дробно-линейных функций138
26.2. Интегрирование дифференциальных биномов................................... |
139 |
26.3. Интегралы, содержащие квадратный корень из квадратного |
|
трехчлена................................................................................................. |
139 |
26.4. Решение некоторых типовых задач, рассматриваемых в аудитории140
26.5. Задачи для самостоятельного решения................................................ |
143 |
ЗАНЯТИЕ 27 |
|
27. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ......... |
144 |
27.1. Простейшие методы интегрирования.................................................. |
144 |
27.2. Тригонометрические подстановки....................................................... |
145 |
27.3. Универсальная тригонометрическая подстановка ............................. |
145 |
27.4. Решение некоторых типовых задач, рассматриваемых в аудитории145
27.5. Задачи для самостоятельного решения................................................ |
148 |
ЛИТЕРАТУРА................................................................................................. |
148 |
7 |
|

ЗАНЯТИЕ 1.
1.ФУНКЦИЯ И СПОСОБЫ ЕЕ ЗАДАНИЯ
1.1.Функция
Определение 1.1 Величину y называют функцией переменной величины
x , если каждому числовому значению x , принадлежащему некоторой области его изменения D x D , соответствует по данному закону (пра-
вилу) единственное определенное значение величины y .
Переменную величину x называют независимой переменной (или аргументом x ).
Область изменения аргумента x называют областью определения функ-
ции y , а множество числовых значений функции y называют областью ее
значений и обозначают E .
Тот факт, что величина y является функцией величины x , обозначают символической записью y f (x), x D , где буква f обозначение закона
(правила), применив который к аргументу x , находят соответствующее ему значение функции y . Говорят также, что функция f отображает множество
D на множество E. Область определения функции D должна быть задана. Если этого нет, то в таких случаях подразумевают так называемую естественную область определения, т.е. множество тех значений аргументаx , при которых функция y будет существовать.
Например,пусть y log2 x 1 .Изэлементарнойматематики,известно,
что x 1 0 x 1. Это и будет естественная область определения D : x 1; .
Если функция f отображает множество D на множество E , а функция g отображает множество E на множество G , то можно рассматривать функцию z g f x , которую называют сложной функцией переменной z от аргумента x , или суперпозицией функций f и g .Она определена на D и отображает D на G .
Определения 1.2
a) Функцию y f x называют четной, если |
f x f |
x . |
б) Функцию y f x называют нечетной, если |
f x f x или |
|
f x f x . |
|
|
в) Функцию y f x , определенную на всей числовой оси, называют перио-
дической,еслисуществуеттакоепостоянноечисло l ,чтопривсяком x будет верно f x l f x . Наименьшее из таких положительных значений l
называют основным периодом T функции или просто периодом.
8
1.2.Основные способы задания функции
Кним относятся: табличный, описательный, графический, аналитический (явное, неявное), параметрическое задание функций. Рассмотрим два из них.
Описательный способ
При таком способе зависимость между аргументом x и функцией y выражается словесным описанием. Например, y наибольшее целое число, не превосходящее x . Эту функцию обозначают y x и называют функция антье (entier), т.е. целый.
x 2 |
x 4,2 |
x 1,5 |
Так имеем: |
, |
, |
y 2 2 |
y 4,2 4 |
y 1,5 2 |
Параметрический способ
При таком способе и аргумент x и функция y связаны между собой через третью переменную величину – параметр t (наиболее употребительное
|
|
|
x (t) |
,t ; |
|
|
|
обозначение). |
|
|
|
||||
|
|
|
y t |
|
|
|
|
Здесь каждому числовому значению параметра t0 из области его измене- |
|||||||
|
|
|
|
|
x |
(t ) |
|
|
ставятся в соответствие числовые значения |
|
0 |
величин |
|||
ния t ; |
|
0 |
|||||
|
|
|
|
|
y0 |
t0 |
|
|
|
|
|
|
|
|
|
x и y . |
|
Это соответствие можно рассматривать как функцию y от x (или |
|||||
x как |
функцию y ). |
Предлагается следующий способ |
схематического |
||||
(эскизного) построения такого графика. Пусть x t2 .
y t3
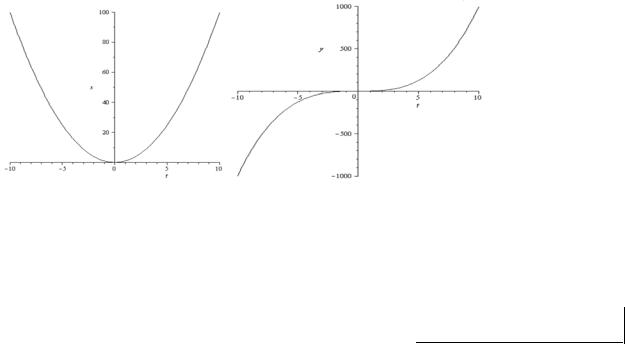
1-ый шаг: строим график x t2 . Это известная парабола (Рис. 1.1).
Рис. 1.1 Рис. 1.2
2-ой шаг: строим график y t3 . (Кубическая парабола) (Рис.1.2).
3-ий шаг: составляем таблицу изменений всех переменных
|
|
y |
t |
x |
|
|
|
|
9
|
|
;0 |
;0 |
;0 |
|
|
|
Возрастает |
Возрастает |
Убывает |
|
|
|
0; |
0; |
0; |
|
|
|
Возрастает |
Возрастает |
Возрастает |
|
|
|
|
Замечаем также, что x 0при всех значениях t , а значит, при двух противоположных значениях t (т.е. при одном и том же значении x ) будем получать два противоположных значения y .
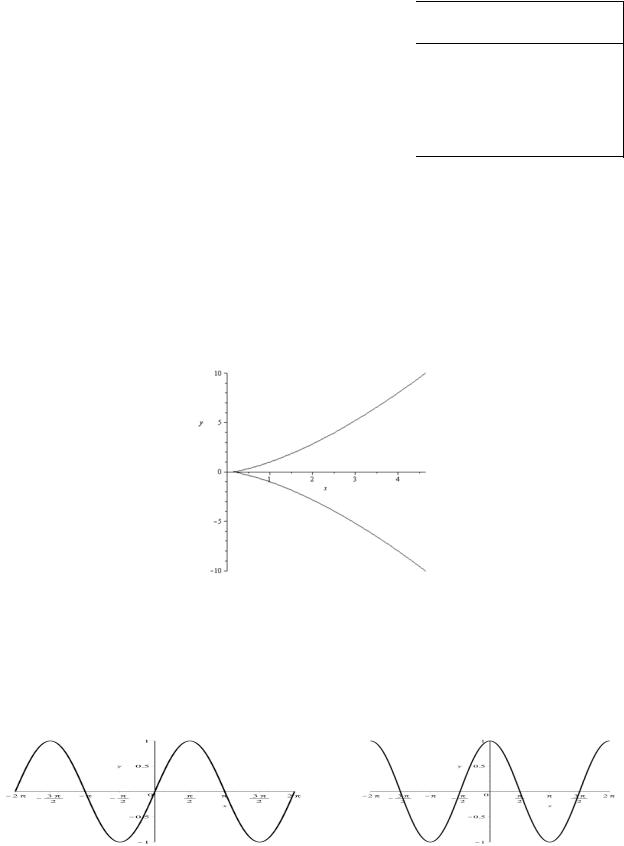
Следовательно, график зависимости y от x будет представлять так
называемую двузначную функцию и будет симметричен относительно оси OX . Рассматривая только два последних столбца таблицы (тем самым изменение y от x ), можно построить следующий схематический график зависимости
y от x (Рис. 1.3).
Рис. 1.3
1.3. Графики элементарных функций
Приведем графики основных элементарных функций.
y sinx |
1 y 1 |
y cosx 1 y 1 |
y tgx |
y ctgx |
10
