кр по алегебре
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
Московский технический университет связи и информатики
________________________________________________________________
Е. В. Ильина, А. В. Куприн, С. А. Маненков, С. М. Фроловичев
КОНТРОЛЬНЫЕ РАБОТЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
И ЛИНЕЙНОЙ АЛГЕБРЕ
Москва 2019
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
Московский технический университет связи и информатики
________________________________________________________________
Е. В. Ильина, А. В. Куприн, С. А. Маненков, С. М. Фроловичев
КОНТРОЛЬНЫЕ РАБОТЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
И ЛИНЕЙНОЙ АЛГЕБРЕ
Москва 2019
УДК 51 (075.8)
Ильина Е. В., Куприн А. В., Маненков С. А., Фроловичев С. М. Кон- трольные работы и методические указания по аналитической геометрии и линейной алгебре: учебно-методическое пособие / МТУСИ. — М., 2019 –
36 с.
Сборник контрольных работ содержит задания по основным разделам курса аналитической геометрии и линейной алгебры для направлений под-
готовки 11.03.01, 11.03.02, 09.03.01, 09.03.02. Вместе с пособиями [1–2] яв-
ляется частью учебно-методического комплекса по указанной дисциплине. Задачи разбиты на 30 однотипных вариантов для выдачи СИДЗ.
Список лит. 2 назв.
Издание одобрено Советом ОТФ-1 в качестве учебно-методического посо- бия. Протокол №1 от 20.09.2018г.
Рецензент: А. Г. Кюркчан, д. ф.-м. н., профессор (МТУСИ)
© Московский технический университет связи и информатики (МТУСИ), 2019 г.
Задания к вариантам
1.Исследовать систему линейных уравнений на совместность, найти об- щее решение, указать фундаментальную систему решений соответствую- щей однородной системы и частное решение данной неоднородной систе- мы.
2.Решить матричное уравнение.
3.Привести уравнение кривой второго порядка к каноническому виду, оп- ределить тип кривой, найти координаты фокусов, вершин, уравнения ди- ректрис, уравнения асимптот (для гиперболы) и построить эту кривую.
4.Решить задачу о кривой второго порядка.
5. Заданы точки A, B, C и D . Найти: 1) скалярное произведение ( AC, AD) и угол ABC ; 2) векторное произведение [ AB, CD]; 3) смешанное произве-
дение AB × AC × AD и объем пирамиды ABCD ; 4) проекцию точки A на прямую BD ; 5) уравнения плоскостей ABC , ABD и угол между этими плоскостями; 6) площадь треугольника BCD ; 7) расстояние от точки B до плоскости ACD ; 8) канонические уравнения перпендикуляра, проведенно- го из точки A на плоскость BCD , и проекцию точки A на эту плоскость; 9) параметрические уравнения прямой DM , где M — точка пересечения медиан треугольника ABC .
6.Найти матрицу линейного оператора A в указанном базисе линейного пространства L .
7.Матрица линейного оператора A задана в базисе {e1, e2 , e3} . Указать матрицу T перехода к новому базису { f1, f2 , f3} , вычислить обратную мат-
рицу T −1 и найти матрицу оператора в новом базисе по формуле Aɶ =T −1AT .
8. Найти собственные значения и собственные векторы матрицы A . Ука- зать матрицу T перехода к новому базису, в котором матрица Aɶ этого преобразования имеет диагональный вид. Сделать проверку, вычислив матрицу Aɶ .
9. Для данной квадратичной формы записать ее матрицу A , привести к ка- ноническому виду методом Лагранжа, проверить равенство Aɶ =T T AT (где T T означает транспонированную матрицу перехода T ), вычислить кано- нические коэффициенты через угловые миноры матрицы A .
10. Привести уравнение кривой второго порядка к каноническому виду ор- тогональным преобразованием, определить тип кривой и координаты ее фокусов.
3
Вариант 1
|
x1 + 3x2 + 5x4 = 9, |
|
|
2 |
−5 |
3 |
|
|
|
|
||||
|
2x - 5x + 5x - x =1, |
|
|
|
4 |
10 6 |
|
|||||||
|
1 |
2 |
3 5 |
|
X × |
|
-6 15 |
-9 |
|
|
- |
|||
1. |
|
|
|
2. |
|
|
= |
-6 |
15 -9 |
. |
||||
3x1 + x2 + x3 + 5x4 −5x5 = 4, |
|
|
|
2 |
-5 |
3 |
|
|
|
|||||
|
3x - 4x - 4x = -5. |
|
|
|
|
|
|
|
|
|||||
|
2 |
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
3.4x2 - 4x -12 y - 5 = 0 .
4.Составить каноническое уравнение гиперболы с фокусами F1 (−1, 2) и F2 (9, 2) , если расстояние между ее вершинами равно 6.
5.A(4, 1, −8), B (1, −2, 1), C (−5, −8, 4), D (−2, 4, −2).
6.Ln –линейное пространство многочленов, порядок которых не превыша-
x
ет n , с базисом {1, x,..., xn }. Ap = ∫ p(t +1)dt , где p( x) L4 , Ap L5 .
0
|
50 |
−10 |
−20 |
|
|
f = e + e + 2e , |
|||||
7. A = |
|
|
|
|
|
|
|
1 |
1 |
2 |
3 |
|
20 |
0 |
40 |
|
, |
f2 = 2e1 - e2 - e3 , |
|||||
|
|
-30 10 |
30 |
|
|
f |
3 |
= -e + e - 2e . |
|||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
9. x2 |
- 4x x |
+ 2x x |
+ 6x2 |
+ 2x2 |
. 10. 5x2 |
+ 6xy |
||
1 |
1 |
2 |
1 |
3 |
2 |
3 |
|
|
Вариант 2
|
|
2 |
−1 |
−2 |
|
8. A = |
|
-1 |
2 |
2 |
|
|
. |
||||
|
|
-2 |
2 |
5 |
|
|
|
|
+ 5 y2 -16x -16 y -16 = 0 .
2x + 5x - x - 5x + x = 9, |
|
1 |
1 |
|
|
|
|||||
|
1 |
2 3 |
4 5 |
|
|
1 |
-1 |
|
4 |
2 |
|
x1 - 5x2 + x3 + x4 - 2x5 = 9, |
2. |
X × |
|
||||||||
1. |
|
15x1 + 4x4 - x5 = 70, |
|
-2 |
= |
|
. |
||||
|
|
|
|
2 |
|
|
5 |
-1 |
|||
|
|
5x1 + x4 = 24. |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|||||
|
|
|
|
|
|
||||||
3.2x2 + 3 y2 + 20x + 6 y + 29 = 0 .
4.Составить каноническое уравнение параболы с вершиной в точке
A(2, −1) и фокусом F (4, −1) .
5.A(−19, 17, −20), B (−1, −7, 10), C (11, −13, 4), D (−7, −1, −8).
6.L – пространство геометрических векторов с базисом {i , j , k }.
Ax = [a,[b , x]] , где x L , |
a ={1,1, 0} |
и b ={1,1,1} . |
|
|
|
|
|
||||||||||
|
−2 5 |
−6 |
|
f = 2e + 2e − 2e , |
|
−4 |
2 |
7 |
|||||||||
7. A = |
|
2 |
3 |
4 |
|
, |
|
1 |
|
1 |
2 |
3 |
8. A = |
|
1 -3 |
|
|
|
|
|
|
|
f2 = 3e1 + e3 , |
|
|
-1 . |
|||||||||
|
|
0 |
-4 |
2 |
|
|
|
f |
3 |
= e - e + 2e . |
|
|
-4 |
4 |
7 |
||
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
9. -4x12 + 8x1 x2 +10x1 x3 - 2x22 -10x2 x3 - 5x32 . 10. 2xy + 2x + 2 y −3 = 0 .
4
Вариант 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 + 3x2 + x4 = 5, |
|
|
|
|
|
|
|
|
|
|||
|
2x1 - x2 + x3 - x5 =1, |
1 |
1 |
-1 -1 |
|
-4 |
2 |
|
|||||
|
× X = |
. |
|||||||||||
1. |
|
|
|
2. |
1 |
-1 |
1 -1 |
|
-2 |
4 |
|
||
3x + x + x + x - x = 4, |
|
|
|||||||||||
|
1 2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
2x + 7 x |
+ 2x |
=12. |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
3.9x2 -16 y2 + 90x + 32 y - 367 = 0 .
4.Составить каноническое уравнение эллипса по его директрисам x =1,
x =13 и малой полуоси b = 2
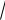2 , зная, что его центр лежит на прямой x −2 y =3 .
5.A(10, 9, -2), B (-11, -12, 19), C (-18, -5, 12), D (3, 2, -9).
6.L – линейное пространство функций вида y( x) = c1ex + c2 xex + c3 x2ex с
базисом {ex , xex , x2ex }. Ay = y(x +1) − y(x −1) , где y(x) L .
|
6 |
2 |
-2 |
|
f = e - e , |
|||||
7. A = |
|
2 -4 |
4 |
|
, |
1 |
1 |
2 |
||
|
|
f2 = e2 - e3 , |
||||||||
|
|
0 |
-6 |
2 |
|
|
f |
3 |
= e + e . |
|
|
|
|
|
|
|
|
|
1 |
3 |
|
9. -x12 - 6x1x2 - 2x1 x3 + 4x22 + 8x2 x3 + 2x32 .
Вариант 4
|
2 |
1 |
-1 |
8. A = -1 |
4 |
-1 . |
|
|
-2 |
2 |
|
|
1 |
||
10. 3x2 + 4xy -10x -12 y + 2 = 0 .
|
x1 + 2x2 - x3 + x4 + x5 = 0, |
|
1 |
2 |
4 |
|
|
|
|
|
|
||||
2x + x |
+ x - 3x + 5x =10, |
|
2 |
2 |
2 |
|
|||||||||
|
1 2 |
|
3 |
4 |
5 |
2. X × 1 |
|
|
|
|
- |
|
|||
1. |
3x + 3x |
- 7 x |
+ 9x |
= 20, |
-4 |
-2 |
= |
0 |
6 |
7 |
. |
||||
|
1 |
3 |
4 |
5 |
|
|
-2 |
2 |
-2 |
|
|
|
|
|
|
|
3x - 3x |
+ 5x |
- 3x = -10. |
|
|
|
|
|
|
|
|||||
|
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
3.16x2 + 25 y2 + 32x -100 y - 284 = 0 .
4.Составить каноническое уравнение гиперболы с вершиной в точке
A(4, 1) и асимптотами 2x −3y +1 = 0 и 2x +3 y −5 = 0 .
5.A(-3, 3, -2), B (-3, 1, -1), C (0, -2, -1), D (2, 1, -1).
6.L – линейное пространство квадратных матриц второго порядка с бази-
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
× X T , где |
|||
сом |
|
, |
|
|
, |
|
, |
. |
A( X ) = |
1 |
|
× X + |
0 |
1 |
|
|
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
2 |
|
|
|
|
|||
X L . Здесь X T |
– транспонированная матрица X . |
|
|
|
|
|
|
|||||||||
5
|
−1 |
3 |
−5 |
|
|
|
f1 = e1 − e2 , |
|
−3 |
5 |
7 |
||||
7. A = |
|
2 |
6 |
-2 |
|
, |
|
|
= e1 + e2 - 2e3 , |
8. A = |
|
-1 3 |
1 |
|
|
|
|
f2 |
|
. |
|||||||||||
|
|
1 |
5 |
-3 |
|
|
f |
3 |
= 2e - e + e . |
|
|
-3 |
3 |
7 |
|
|
|
|
|
|
|
|
|
1 2 3 |
|
|
|
|
|
|
|
9. -5x12 - 4x1x2 +10x1x3 - 2x22 +10x2 x3 - 5x32 . 10. x2 + 2xy + y2 + 8x + 4 y - 7 = 0 .
Вариант 5
|
2x1 + x2 - x3 - x4 + x5 = 5, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x1 - x2 + x3 + x4 - 2x5 = -3, |
|
1 |
-1 |
2 |
0 |
2 |
4 |
|||||||||
1. |
3x + 3x |
- 3x - 3x |
+ 4x |
=13, |
2. |
|
-1 |
-1 |
0 |
2 |
|
× X = |
0 |
-2 |
. |
||
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
4x + 5x |
- 5x - 5x |
+ 7 x |
= 21. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
3.16x2 - 9 y2 - 64x -18 y +199 = 0 .
4.Составить каноническое уравнение эллипса с вершинами A(2, 3) и
B(5, 1) , если известно, что оси эллипса параллельны координатным осям. Чему равен эксцентриситет эллипса?
5.A(11, −8, 6), B (11, −2, 3), C (0, 7, 3), D (−4, −2, 3).
6.L –линейное пространство многочленов, порядок которых не превыша-
ет трех |
|
с базисом |
{1, |
x |
, |
x2 |
, |
x3 |
} |
|
Ap |
= ( |
x |
-1) |
2 |
p¢¢ |
|
x |
) + |
|
x |
-1) |
p¢ |
x |
) + 2 |
p |
|
x |
|
|||||||||||
|
|
, |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
( |
|
2( |
|
( |
|
( |
|
) , |
||||||||||||||
где p(x) L . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
8 −2 |
|
|
|
f = e − e + e , |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 −2 |
|||||||||||||||||||
|
|
2 -4 -6 |
|
|
|
|
|
1 |
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-6 |
|
-4 6 |
|
|||||||||
7. A = |
|
, f2 = -e1 + e2 + e3 , |
|
|
|
|
|
8. |
|
|
A = |
|
|
. |
||||||||||||||||||||||||||
|
|
6 2 -2 |
|
|
f |
3 |
= -2e + e - e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
|
-5 7 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. x2 |
+ 4x x |
+10x x |
|
+ 2x2 + 8x x |
+ 5x2 . |
10. 7 x2 |
- 24xy - 38x + 24 y +175 = 0 . |
|||||||||||||||||||||||||||||||||
1 |
|
|
1 |
2 |
1 |
3 |
|
2 |
|
|
|
|
2 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x1 - 6x2 + 2x3 - 2x4 +16x5 = 7, |
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
4 |
|
|
|
|
||||||||||||||||||||||
|
|
|
- 3x2 + 2x3 + x4 - 3x5 = 4, |
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
7 10 |
|
|
|
|
|
||||||||||||||||
|
x1 |
|
|
|
|
|
|
|
|
|
|
× X = |
. |
|
|
|
|
|||||||||||||||||||||||
1. |
|
|
|
|
|
|
|
+ x4 = |
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2x1 - 7 x2 + 4x3 |
9, |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
8 |
|
|
|
13 18 |
|
|
|
|
|
||||||||||||||
|
|
|
- 4x2 + 2x3 + 3x5 = 5, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
4 |
6 |
|
|
|
|
|||||||||||||||||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3.9x2 + 4 y2 - 36x + 8 y + 4 = 0 .
4.Составить каноническое уравнение гиперболы, если ее асимптоты за- даются уравнениями x −3y +7 = 0 и x +3y −5 = 0 , а одна из директрис
совпадает с осью ординат.
6
5.A(22, −14, 23), B (4, 10, −7), C (−8, 16, −1), D (10, 4, 11).
6.Ln –линейное пространство многочленов, порядок которых не превыша-
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
ет n , с базисом {1, |
x,..., xn }. Ap = ∫(3t + 2) p(t)dt , где p( x) L3 , |
Ap L5 . |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 −2 |
|
|
f = 2e + e , |
|
|
|
|
4 −1 |
|
−1 |
|
|
|||||||||
|
|
2 |
1 −1 |
|
|
|
1 |
1 |
3 |
|
|
|
|
A = |
|
−1 4 |
|
1 |
|
|
|
||
7. A = |
|
, |
|
f2 = e2 − 2e3 , |
|
8. |
|
|
|
. |
|
|
|||||||||||
|
|
1 |
−1 2 |
|
f |
3 |
= e − e + 2e . |
|
|
|
|
|
−1 1 |
|
4 |
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9. 5x2 |
− 6x x |
− 6x x |
+ 3x2 |
+ 6x x |
+ 3x |
2 . |
10. 3x2 − 2xy + 3 y2 − 6x + 2 y +1 = 0 . |
||||||||||||||||
1 |
|
1 |
2 |
1 |
3 |
2 |
|
2 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x1 + x2 − x3 + x5 = −1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3x1 − x2 − 7 x3 |
− 4x4 −3x5 =11, |
|
|
1 |
2 |
3 |
|
4 |
|
-2 |
-4 |
|
||||||||||
1. 7 x − x |
−15x |
−8x |
+ 6x |
= 32, |
|
2. |
3 |
6 |
9 |
12 |
× X = |
|
-6 |
-12 |
. |
||||||||
|
|
1 |
2 |
|
3 |
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x −3x − 2x − x = 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
2 |
3 |
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.4x2 + 20x −12 y + 43 = 0 .
4.Составить каноническое уравнение гиперболы с центром в точ-
ке (−15, 0) и одним из фокусов, расположенном в начале координат, если гипербола отсекает от оси ординат хорду длиной 32 .
5.A(−5, 4, −2), B (4, −2, 4), C (4, −5, 10), D (−2, 1, −5).
6.L – линейное пространство квадратных матриц второго порядка с бази-
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
3 |
0 |
×(X + X T ), где X L . |
||||||||||
сом |
0 |
0 |
|
, |
0 |
0 |
|
, |
1 |
0 |
|
, |
0 |
1 |
. |
A( X ) = |
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Здесь X T |
– транспонированная матрица X . |
|
|
|
||||||||||||
|
|
1 |
|
−3 7 |
f1 = 3e1 − e2 + 2e3 , |
2 |
4 |
4 |
||||||||
7. |
A = 1 |
|
2 |
−3 , |
f2 = −e1 + 2e2 + e3 , |
8. A = 4 |
2 |
−4 . |
||||||||
|
|
5 |
|
0 |
5 |
|
|
f |
3 |
= e − e + e . |
4 |
−4 2 |
||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
9. |
3x2 |
− 6x x |
+8x x + x2 |
− 6x x |
+ 4x2 . |
10. 5x2 − 2xy + 5 y2 |
+10x − 2 y +1 = 0 . |
|||||||||
|
1 |
|
1 |
2 |
1 |
3 |
2 |
|
|
2 |
3 |
3 |
|
|
|
|
7
Вариант 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x1 + 3x2 |
+ 6x4 |
=10, |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
2x1 - 6x2 + 6x3 - x5 =1, |
7 14 |
21 |
||||||||||||
7 |
14 |
21 |
|
||||||||||||
1. |
|
|
+ 6x4 |
2. X × |
= |
-6 |
-12 |
-18 |
. |
||||||
3x1 + x2 + x3 |
−6x5 = 4, |
|
-3 |
-6 |
-9 |
|
|
|
|||||||
|
2x −10x +11x + 4x = 7. |
|
|
|
|
|
|
|
|||||||
|
1 |
2 |
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
3.16x2 - 9 y2 - 64x - 54 y -161 = 0 .
4.Составить каноническое уравнение эллипса с фокусами F1 (−2, 1) , F2 (4, 1) и директрисой x =5 .
5. |
A(4, 2, −6), B (1, −1, 3), C (−5, −7, 6), D (−2, 5, 0). |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
L – пространство геометрических векторов плоскости с базисом {i , j}. |
|||||||||||||
A – оператор симметрии относительно прямой x |
|
− y = 0 . |
|
|||||||||||
3 |
|
|||||||||||||
|
5 |
|
3 -1 |
|
|
f = 2e + e , |
|
|
2 -2 |
2 |
||||
|
A = -2 |
|
0 -2 |
|
|
1 |
2 |
3 |
|
|
A = -2 5 |
-4 . |
||
7. |
|
, |
|
f2 = e1 - e3 , |
8. |
|
||||||||
|
4 |
|
-3 1 |
|
f |
3 |
= e + 2e + e . |
|
|
2 -4 |
5 |
|||
|
|
|
|
|
|
|
|
1 |
2 3 |
|
|
|
|
|
9. |
-3x2 - 6x x |
+ 6x x |
+ 6x x |
+ x2 . |
10. 4x2 |
- 2xy + 4 y2 -10x +10 y +1 = 0 . |
||||||||
|
1 |
1 |
2 |
1 |
3 |
2 |
3 |
3 |
|
|
|
|
|
|
Вариант 9 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x1 + 2x2 - x3 + 8x4 + x5 = -4, |
|
1 |
1 |
3 |
2 |
|||||||
|
|
3x1 + x2 + 2x3 - x4 - 3x5 = 3, |
|
|
1 |
-1 |
|
|
-1 |
0 |
|
|||
|
|
2. |
|
|
× X = |
. |
||||||||
1. |
|
|
|
|
|
|
|
|
|
|||||
-2x1 + 6x2 - 8x3 + 34x4 + 5x5 = -22, |
|
|
4 |
2 |
|
|
8 |
6 |
|
|||||
|
2x + 9x |
- 7 x |
+ 41x |
+ 3x = -23. |
|
|
5 |
-1 |
|
3 |
4 |
|
||
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
3.5x2 + 9 y2 - 30x +18 y + 9 = 0 .
4.Составить каноническое уравнение гиперболы с фокусами F1 (1, −1) и F2 (1, 5) , угол между асимптотами которой равен 600 .
5.A(-4, 6, 1), B (1, -4, 6), C (6, 6, -9), D (1, -4, -4).
8
6. |
L – линейное пространство функций вида y(x) = c1 + c2 cos x + c3 sin x с |
|||||||||||||||||||
базисом {1, cos x, sin x} . |
|
|
′′ |
′ |
|
|
|
|
|
|||||||||||
Ay = y |
( x) − |
2 y ( x) + 2 y( x) , где y(x) L . |
|
|
||||||||||||||||
|
|
2 |
0 |
|
|
1 |
|
|
f = 3e + e + 2e , |
|
5 −2 |
−2 |
||||||||
|
A = |
|
3 |
5 |
|
-5 |
|
, |
|
1 |
|
1 |
2 |
3 |
|
|
-2 4 |
0 |
|
|
7. |
|
|
|
f2 = -2e1 + 2e2 + e3 , |
8. |
A = |
. |
|||||||||||||
|
|
|
2 |
2 |
|
-1 |
|
|
f |
3 |
= -e + 3e + 2e . |
|
|
-2 0 |
6 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
9. |
-4x2 +16x x |
|
- 3x2 |
- 20x2 |
. 10. 7 x2 |
+16xy - 23 y2 |
-14x -16 y + 32 = 0 . |
|||||||||||||
|
1 |
|
|
1 |
2 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
Вариант 10 |
|
|
|
|
|
|
|
|
|
|
|
x1 + 3x2 − x3 − 6x4 + 3x5 = 3, |
1 |
1 |
0 |
|
|
|
|
||||
−2x1 + x2 − x3 |
−3x4 − x5 |
= −1, |
7 |
4 3 |
|||||||
1. |
|
−3x3 |
|
2. X × |
1 |
-2 |
3 |
= |
1 |
-2 3 |
. |
x1 + 2x2 |
+ x4 + 2x5 = 2, |
|
3 |
|
|
|
|||||
|
−4x + x − 4x + x + x =1. |
6 |
3 |
|
|
|
|
||||
|
1 |
2 |
3 4 |
5 |
|
|
|
|
|
|
|
3.x2 + 4x - 4 y + 8 = 0 .
4.Составить каноническое уравнение эллипса с фокусами F1 (−1, 1) , F2 (3, 1) и директрисой x =5 .
5.A(19, −11, 18), B (−2, 10, −3), C (5, 3, −10), D (12, −18, 11).
6.L –линейное пространство функций вида y(x) = c1 + c2 cos x + c3 sin x с
базисом {1, cos x,sin x} |
. Ay = y(x +π / 6) − y(x −π / 6) + 2 y(x) , где y(x) L . |
||||||||||||||||||||
|
|
|
1 |
|
−2 |
3 |
|
|
|
f = e + 2e , |
|
|
3 |
−2 |
0 |
||||||
|
A = |
|
-4 |
|
5 -6 |
|
|
|
|
1 |
2 |
3 |
|
8. A = |
|
|
-5 |
|
|
||
7. |
|
|
|
, |
|
|
f2 = e1 - e3 , |
|
|
2 |
2 |
. |
|||||||||
|
|
|
|
7 |
|
-8 |
9 |
|
|
f |
3 |
= e + e + 2e . |
|
|
0 |
-4 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
9. |
8x2 |
+16x x +16x x |
|
+ 4x2 |
+ 8x x |
+ 8x2 . |
10. xy − 2x − 2 y + 2 = 0 . |
||||||||||||||
|
1 |
|
|
|
1 |
2 |
1 |
3 |
|
2 |
2 |
3 |
3 |
|
|
|
|
|
|
|
|
9