линейная алгебра и агалитич геом

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

А.В. Куприн, С.М. Фроловичев

«Рекомендовано УМО по образованию в области Инфокоммуникационных технологий и систем связи в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки 11.03.02 – Инфокоммуникационные технологии и системы связи (уровень высшего образования – бакалавриат».

Протокол № 84 от 28.05.2015 г.

КУРС ЛЕКЦИЙ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

И ЛИНЕЙНОЙ АЛГЕБРЕ

Учебное пособие для направления 11.03.02

Москва 2016

УДК 51 (075.8)

Куприн А.В., Фроловичев С.М. Курс лекций по аналитической геометрии и линейной алгебре: Учебное пособие / МТУСИ. – М., 2016. – 88 с.

Учебное пособие предназначено для студентов первого семестра технических высших учебных заведений, обучающихся по программам бакалавров направления подготовки 11.03.02 «Инфокоммуникационные технологии и системы связи».

Ил. 33, список лит. 7 назв.

Рецензенты: М.В.Карасев, д. ф.-м. н., профессор (ВШЭ МИЭМ) А.Г.Кюркчан, д. ф.-м. н., профессор (МТУСИ) Л.М.Баскин, д.ф.-м.н., профессор (С.-ПбУ информационных

технологий)

© Московский технический университет связи и информатики, 2016 г.

СОДЕРЖАНИЕ

Введение…………..…………………………………………………………….. 6

Раздел I. Матрицы и определители

Лекция 1. Определители второго и третьего порядка, их свойства. Миноры, алгебраические дополнения. Разложение определителя по элементам строки или столбца. Определитель n -го порядка и его вычисление………. 7 Лекция 2. Матрицы, равенство матриц, действия над матрицами, транспонирование матриц, обратная матрица……………………………………… 11

Раздел II. Системы линейных уравнений

Лекция 3. Системы линейных уравнений. Совместность и несовместность, определенность. Эквивалентность систем. Матричная форма записи систем. Система n уравнений с n неизвестными. Решение при помощи обратной матрицы. Формулы Крамера. Метод Гаусса. Элементарные преобразова-

ния матриц………………………………………………………………………. 15

Лекция 4. Ранг матрицы. Неизменность ранга при элементарных преобразованиях. Ступенчатые матрицы и их ранг. Теорема Кронекера-Капелли. Критерий определенности системы. Однородные системы линейных уравне-

ний…………………………………………….…………………………………. 19

Лекция 5. Фундаментальная система решений однородной системы уравнений. Общее решение неоднородной системы……………………….. 24

Раздел III. Векторная алгебра

Лекция 6. Геометрические векторы. Линейные операции над векторами и их свойства. Линейная зависимость векторов. Коллинеарные и компланар-

ные векторы.………………………………….………………………………… 27

Лекция 7. Базис на плоскости и в пространстве. Координаты вектора. Декартова прямоугольная система координат. Координаты точки. Деление отрезка в заданном отношении. Преобразование координат при параллельном переносе и повороте системы…………………………………………….. 32

3

Лекция 8. Скалярное, векторное и смешанное произведение векторов и их вычисление в декартовых координатах…………………………………….36

Раздел IV. Уравнения первого порядка и их геометрические образы

Лекция 9. Уравнение линии на плоскости. Прямая линия на плоскости. Уравнение поверхности. Уравнение плоскости в пространстве. Пучок плос-

костей…………………………………………………………………………… 40

Лекция 10. Уравнения линии в пространстве. Различные виды уравнений прямой линии в пространстве. Взаимное расположение двух прямых, прямой и плоскости в пространстве………………………………………… 44

Раздел V. Уравнения второго порядка и их геометрические образы

Лекция 11. Кривые второго порядка. Эллипс. Гипербола. Парабола. Общее определение кривых второго порядка…………………………………… 49

Лекция 12. Поверхности второго порядка. Эллипсоид. Гиперболоиды. Параболоиды. Цилиндрические и конические поверхности. Вырожденные случаи.……………………….............................................................................. 54

Раздел VI. Линейные пространства

Лекция 13. Линейные пространства. Линейная зависимость и независимость векторов линейного пространства. Базис и размерность линейного пространства. Координаты векторов в базисе. Преобразование координат векто-

ра при изменении базиса……………………………………………………….. 58

Лекция 14. Скалярное произведение в линейном пространстве. Евклидово пространство. Норма вектора, свойства нормы, угол между двумя векторами евклидова пространства. Ортогональные векторы. Процесс ортогона-

лизации…………………………………………………………………….......... 62

Лекция 15. Линейные операторы. Матрица линейного оператора. Преобразование матрицы линейного оператора при переходе к новому бази-

су……………..……………………………………………………………......... 67

Лекция 16. Собственные значения и собственные векторы линейного оператора и их вычисление. Линейная независимость собственных векторов с различными собственными значениями……..……………………………. 70

4

Лекция 17. Оператор простой структуры. Матрица оператора в базисе из собственных векторов. Самосопряженные операторы. Собственные значения и собственные векторы самосопряженного оператора………………………. 75 Лекция 18. Билинейные и квадратичные формы………………………. 77

Список литературы……………………………………………………... 84 Предметный указатель…………………………………………………. 85

5

Введение

Курс аналитической геометрии и линейной алгебры является важной частью математической подготовки бакалавров телекоммуникаций. Действующими программами предусмотрено значительное сокращение лекционных часов по этому предмету, вследствие чего изложить весь необходимый материал в аудитории не представляется возможным. Поэтому возникла потребность в учебном пособии, призванном помочь студентам самостоятельно изучить темы, не включенные в аудиторный лекционный курс. Основой настоящего пособия стал электронный учебник, в работе над которым, помимо авторов этой книги, принимал участие доцент О.М. Смелянский. Кроме того, отдельным разделам аналитической геометрии и линейной алгебры были посвящены пособия и методические указания [1] – [4], ранее изданные в МТУСИ.

Материал разбит на 18 лекций — по количеству учебных недель в первом семестре. Последовательность изложения соответствует рабочим программам и позволяет студентам подготовиться к текущим практическим занятиям, промежуточным аттестациям, проводимым в форме тестирования и контрольных работ, а также к экзамену. Издание снабжено предметным указателем. В тексте используются символы алгебры логики, значение которых известно студентам первого курса.

Вкачестве дополнительной литературы авторы рекомендуют учебники

[5]– [7], где можно найти, в частности, доказательства некоторых теорем, не приведенные в настоящем пособии.

6

Раздел I. Матрицы и определители

Лекция 1

Определители второго порядка. Пусть дана таблица чисел (матрица)

ний и правый нижний углы квадратной матрицы, называется ее главной диагональю. В случае определителя второго порядка, главная диагональ – это

(a,d ).

Свойства определителей.

1) Если матрицу транспонировать, т.е. строки заменить соответствующими столбцами, то величина определителя не изменится:

ны. Любое из дальнейших свойств достаточно проверить только для строк. 2) Перестановка двух строк (столбцов) равносильна умножению опреде-

лителя на −1:

3) Если у матрицы A две одинаковые строки (столбца), то det A = 0 . Это вытекает из свойства 2), т.к. перестановка двух равных строк, с одной стороны, не изменяет определителя, с другой стороны, меняет его знак, т.е. det A = −det A. Из последнего равенства заключаем, чтоdet A = 0 .

7

4) Общий множитель всех элементов одной строки (столбца) можно вынести за знак определителя:

5)Если все элементы некоторой строки (столбца) определителя равны нулю, то сам определитель тоже равен нулю. Это свойство является следствием свойства 4) при k = 0 .

6)Если соответствующие элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю. Это свойство является следствием свойств 3) и 4). Действительно, после вынесения за знак определителя коэффициента пропорциональности мы получим определитель с одинаковыми строками.

7)Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то определитель равен сумме двух определителей, в первом из которых в указанной строке (столбце) расположены первые слагаемые, во втором - вторые слагаемые, а остальные строки (столбцы) этих определителей совпадают с соответствующими строками (столбцами) исходного определителя:

8) Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то определитель не изменится:

9) Если под или над главной диагональю определителя все элементы равны нулю, то определитель равен произведению элементов, расположенных на

Определители третьего порядка.

делителем называется число

Принята следующая нумерация элементов матрицы: первый индекс указывает на номер строки, второй — на номер столбца, на пересечении которых расположен данный элемент.

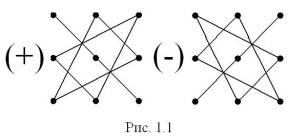
В каждом из шести произведений присутствует только один элемент любого столбца и один элемент любой строки. Чтобы запомнить, какие произведения входят с плюсом, а какие — со знаком минус, удобно иметь в виду правило, изображенное на рис. 1.1.

Разложение определителя по элементам строки (столбца).

Представим определитель третьего порядка в следующем виде:

det A = a11a22a33 +a12a23a31 +a13a21a32 −a11a23a32 −a12a21a33 −a13a22a31 =

= a31(a12a23 −a13a22 ) −a32 (a12a23 −a13a21) +a33 (a11a22 −a12a21) =

делитель второго порядка Mij, который остается после вычеркивания строки

9