
лекции вышмат
.pdfМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
Московский технический университет связи и информатики
________________________________________________________________________
А.Р. Лакерник
КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Учебное пособие
Москва 2021
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
Московский технический университет связи и информатики
________________________________________________________________________
А.Р. Лакерник
КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Учебное пособие для направления подготовки: 11.03.02
Москва 2021
1
УДК 51 (075.8)
Лакерник А.Р. Курс лекций по высшей математике: учебное пособие / МТУСИ. - М., 2021. - 249 с.
Пособие является курсом лекций автора и соответствует учебным планам и рабочим программам по курсу высшей математики для студентов направления 11.03.02 приема 2020 г. Может также быть использовано студентами других направлений МТУСИ. Предназначено для помощи студентам в освоении теоретического материала, проведении самостоятельной работы, подготовке к тестированиям и экзаменам.
Ил. 126
Издание утверждено Методическим советом университета в качестве учебного пособия. Протокол № 1 от 27.10.2020г.
Рецензенты: В.Г. Данилов, д.ф.-м.н., профессор (МТУСИ) А.А. Зайцев, к.ф.-м.н., с.н.с. (МИИГАИК)
© Московский технический университет связи и информатики (МТУСИ), 2021
2
|
ОГЛАВЛЕНИЕ |
|
|
Оглавление. |
3 |
|
Предисловие. |
5 |
|
1 семестр |
|
1. |
Действительные и комплексные числа. |
6 |
2. |
Функции. Предел последовательности и функции. |
11 |
3. |
Бесконечно малые. Основные теоремы о пределах. |
16 |
4. |
Некоторые теоремы о пределах. Замечательные пределы. Сравнение |
|
|
бесконечно малых. |
20 |
5. |
Непрерывность функции в точке и на множестве. |
25 |
6. |
Производная функции. |
30 |
7. |
Дифференциал. Производные и дифференциалы высших порядков. |
35 |
8. |
Теоремы о среднем. Правило Лопиталя раскрытия неопределенностей. |
41 |
9. |
Формула Тейлора. |
46 |
10. |
Возрастание и убывание функции, экстремумы. |
51 |
11. |
Исследование функции и построение ее графика. |
56 |
12. |
Неопределенный интеграл, замена переменной. |
63 |
13. |
Интегрирование по частям. Интегрирование рациональных дробей. |
68 |
14. |
Интегрирование иррациональных и тригонометрических выражений. |
|
|
Определенный интеграл. |
74 |
15. |
Вычисление определенного интеграла. Геометрические приложения. |
80 |
16. |
Функции нескольких переменных. |
88 |
17. |
Функции нескольких переменных (продолжение). |
97 |
|
2 семестр |
|
1. |
Несобственный интеграл. |
105 |
2. |
Гамма – функция. Двойной интеграл, определение, свойства, вычисление. |
111 |
3. |
Тройной интеграл. Замена переменных в двойном интеграле. |
119 |
4. |
Замена переменных в тройном интеграле. Криволинейный интеграл 1-ого |
|
|
рода. |
126 |
5. |
Криволинейный интеграл 2-ого рода. Независимость от формы пути |
|
|
интегрирования. |
131 |
6. |
Скалярное поле: производная по направлению и градиент. Векторное |
|
|
поле: циркуляция вдоль кривой и поток через поверхность. |
138 |
7. |
Формулы Гаусса-Остроградского, Грина, Стокса. Дивергенция и ротор |
|
|
векторного поля. |
146 |
8. |
Операции 2-ого порядка. Специальные векторные поля. Скалярный и |
|
|
векторный потенциал. |
152 |
9.Дифференциальные уравнения 1-ого порядка. Общее и частное решения. Задача Коши. Уравнения с разделяющимися переменными, однородные
уравнения. |
156 |
10. Линейные уравнения первого порядка, уравнение Бернулли, уравнение в |
|
полных дифференциалах. Дифференциальные уравнения высших |
|
порядков. Уравнения, допускающие понижение порядка. |
160 |
11.Свойства решений линейного однородного дифференциального уравнения. Определитель Вронского. Структура общего решения
линейного однородного уравнения. |
165 |
3
12. Решение линейного однородного дифференциального уравнения с |
|
постоянными коэффициентами. Структура общего решения линейного |
|
неоднородного уравнения. |
169 |
13.Решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами и правой частью специального и
произвольного вида. |
173 |
3семестр
1.Числовые ряды. Ряды с неотрицательными членами и членами
|
произвольного знака. Признаки сходимости. |
179 |
2. |
Функциональные и степенные ряды. Область сходимости. Ряды Тейлора |
|
|
и Маклорена. |
187 |
3. |
Ряды Фурье. |
195 |
4. |
Функции комплексного переменного. Предел, непрерывность, |
|
|
производная функции комплексного переменного. |
203 |
5. |
Интеграл от функции комплексного переменного. Интегральная теорема |
|
|
и интегральная формула Коши. |
209 |
6. |
Производные высших порядков аналитической функции. Ряды с |
|
|
комплексными членами, ряды Тейлора и Лорана. |
216 |
7. |
Классификация изолированных особых точек однозначного характера. |
|
|
Вычеты и их нахождение. Основная теорема о вычетах. |
224 |
8. |
Вычисление некоторых интегралов от функций действительного |
|
|
переменного. Операционное исчисление. |
231 |
9. |
Операционное исчисление (продолжение). |
239 |
4
ПРЕДИСЛОВИЕ
В 2020-2021 уч. году на многих специальностях МТУСИ, в частности, на специальности 11.03.02 вводятся новые учебные планы, сильно отличающиеся от предыдущих. В этих планах количество часов на математику существенно сокращено.
Данный курс лекций соответствует новому учебному плану этой специальности. В этот план включена только одна дисциплина «Высшая математика», включающая все математические дисциплины предыдущих планов.
Курс лекций охватывает все эти дисциплины, кроме «Аналитической геометрии и линейной алгебры» и «Дискретной математики», содержание которых отражено в учебных пособиях других преподавателей кафедры Математического анализа МТУСИ.
Следует отметить, что, из-за недостатка времени, лекции 21 и 22 первого семестра обучения будут в аудитории излагаться лишь частично. Остальной материал этих лекций будет предлагаться студентам для самостоятельной проработки. Аналогично, возможно, придется поступать с лекциями 8 и 9 третьего семестра обучения и некоторыми частями других лекций.
С определенной коррекцией данный курс лекций может использоваться и студентами других специальностей МТУСИ.
Курс основан на учебных пособиях А.Р. Лакерника «Высшая математика. Краткий курс. Москва. Логос. 2008, 2011. 525 с.» и «Лекции по математическому анализу и высшей математике. Москва. МТУСИ. 2012. 298 с.». При подготовке курса автор подверг материал пособий очередным сокращениям для возможности изложения в рамках выделенных на предмет часов.
5
|
|
|
|
|
|
1 СЕМЕСТР |
|
||
|
|
|
|
|
|
ЛЕКЦИЯ 1 |
|
||
Обозначения: |
|
|
|
|
|
|
|||
▲и ■ означают соответственно начало и конец доказательства теоремы; |
|
||||||||
– «из предложения a |
следует предложение b |
»; |
|
||||||
a b – «предложения |
a и b равносильны: из a |
следует b и из b следует a »; |
|
||||||
– означает «для любого», «для всякого»; |
|
|
|
||||||
– «существует», «найдется»; |
|
|
|
|
|||||
: – «имеет место», «такое что»; |
|
|
|
|
|||||
A B |
– объединение множеств, |
т.е. множество всех элементов, принадлежащих хотя бы |
|||||||
одному из множеств |
A и B ; |
|
|
|
|
||||
A B |
– пересечение |
множеств, |
т.е. множество |
всех элементов, принадлежащих |
A и B |
||||
одновременно; |
|
|
|
|
|
|
|||
x X ( x X ) – элемент |
x , принадлежащий (не принадлежащий) множеству X ; |
|
|||||||
– пустое множество, т.е. множество, не содержащее ни одного элемента; |
|
||||||||
запись |
A = |
|
a, b, c,... |
означает, что множество |
A |
состоит из элементов a,b, c,... ; |
|
||
|
|
|
|
||||||
последовательность
a |
, n |
n |
|
=1, 2,3,...
будет обозначаться как
a |
|
n |
|
;
факториал числа:
|
|
n |
|
|
|
n! =1 2 3 ... n, 0! =1 |
; |
a |
= a + a |
+... + a |
|
сумма чисел k |
1 |
2 |
n . |
||
|
|
k =1 |
|
|
|
ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА.
Некоторые свойства множества действительных чисел
Множество действительных чисел будем обозначать как R.
Множество R является непрерывным, т.е. если X R, Y R два любые непустые числовые множества такие, что для всех элементов x X, y Y выполняется неравенство
x y, то существует некоторое число a R , такое, что x a y, |
x X, y Y. |
|
Абсолютная величина (модуль) действительного числа: (| a |): |
| a | = a, если а 0 и |
|
| a | = –a, если а 0. Докажем, что | a + b | |
| a | + | b | ; | a – b | | a | – | b |. |
|
▲ a | a | , b | b | a + b | a | + | b |; |
–a | a |, –b | b | – (a + b) | a | + | b | ; |
|
так как | a + b | = a + b или | a + b | = – ( a + b ), то отсюда | a + b | | a | + | b |. |
||
| a | = | (a – b) + b | | a – b | + | b | | a – b | | a | – | b |. ■ |
|
|
Определение 1. Множество X R называется ограниченным сверху (снизу), если все члены |
||
х множества X меньше или равны (больше или равны) некоторого числа b. Множество Х, |
||
ограниченное сверху и снизу, называется просто ограниченным. |
|
|
Определение 2. Пусть множество Х ограничено сверху. Наименьшее из чисел, ограничивающих Х сверху, называется верхней гранью множества Х и обозначается
sup X = sup х . Пусть множество Х ограничено снизу. Наибольшее из чисел,
x X
ограничивающих Х снизу, называется нижней гранью множества Х и обозначается
inf X = inf x .
x X
6
Если верхнюю грань множества Х уменьшить, то она уже не будет ограничивать Х сверху; или если нижнюю грань множества Х увеличить, то она уже не будет ограничивать Х снизу. Поэтому определение 2. равносильно следующему определению:
Определение 3. Число b называется верхней гранью множества, если
а) x X x b; |
б) 0 x X: x b - . |
Число а называется нижней гранью множества, если
а) x X x a ; |
б) 0 x X: x a + . |
Теорема 1. Всякое ограниченное сверху (снизу) непустое множество имеет верхнюю (нижнюю) грань.
▲ Пусть А ограничено сверху, А (т.е. А не является пустым множеством), В – множество всех чисел, ограничивающих А сверху, следовательно, при а А, b В всегда будет верно следующее утверждение: а b . Тогда по свойству непрерывности множества R существует такое с, что а с b, а А, b В. Но это и означает, что с ограничивает А сверху (с а) и является наименьшим среди всех чисел, ограничивающих А сверху (с b). Аналогично доказывается второе утверждение теоремы. ■
Определение 4. Система числовых отрезков
[a
n
,b
n
] , a
n
R, b
n
R, n = 1, 2, 3,…
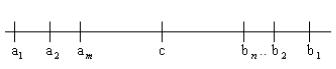
называется системой вложенных отрезков, если a1 a … a n … b n … b b1 (рис.1). 2 2
Теорема 2. (принцип вложенных отрезков). Всякая система вложенных отрезков имеет
хотя бы одну общую точку. |
|
|
|
|
|
▲ Пусть А = {a1 , a 2 ,…}, B = {b |
1 |
,b |
2 |
,…}, следовательно, |
a m b n (рис. 1), m, n N. Тогда |
по свойству непрерывности множества R существует |
такое с R, что выполняется |
||||
неравенство a m c b
n
, m,n N, в частности, a
n
c b
n
, n N. ■
Рисунок 1
Замечание. Для всякой системы вложенных отрезков, по длине стремящихся к 0, общая точка единственна.
▲ Пусть с1 и с 2 – две общие точки и с1 с 2 , тогда длина любого отрезка системы будет не меньше, чем | с 2 - с1 |, что противоречит условию стремления к 0 длин отрезков. ■
Комплексные числа
Определение 5. Комплексным числом z называется пара действительных чисел x и y, которая обычно записывается в виде
z = x + iy, |
(1) |
где i – некоторый символ. Число x называется действительной частью комплексного числа z = x + iy и обозначается x = Re z. Число y называется мнимой частью комплексного числа z = x + iy и обозначается y = Im z .
7

Определение 6. Два комплексных числа называются равными, если у них совпадают действительные и мнимые части.
Определение 7. Комплексное число z = x + iy.
z = x −iy
называется сопряженным к числу
Определение 8. Пусть |
z |
= x +iy |
, z |
= x |
+iy |
– два комплексных числа. Тогда: |
|
1 |
1 |
1 |
2 |
2 |
2 |
||
1) |
z z |
= (x + x ) i(y + y ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
2 |
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) Для определения произведения |
|
z z |
2 |
формально перемножим их, |
используя |
||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||
свойства действительных чисел и принимая, что |
i |
2 |
= i i = −1: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z |
2 |
= (x +iy )(x |
+iy |
) = x x |
− y y +i(x y + y x ) |
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
1 |
2 |
|
2 |
|
1 |
2 |
|
|
1 |
2 |
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
||||
Последнее |
комплексное |
число |
и |
берется |
|
за |
|
определение |
произведения |
||||||||||||||||||||||||||
этого определения, в частности, следует, что |
i |
2 |
= ii |
= −1 (x |
= x |
|
= 0, y |
|
= y |
|
=1). |
||||||||||||||||||||||||
|
|
|
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= i,i |
2 |
= −1,i |
3 |
= −i,i |
4 |
=1,i |
5 |
= i,... |
|||||||
По определению z |
n |
= z z...z (n раз). В частности |
i |
|
|
|
|
||||||||||||||||||||||||||||
обычные
z z |
2 |
. Из |
1 |
3) Для определения частного
z |
|
|
1 |
z |
2 |
|
|
также проведем формальные преобразования, домножая
числитель и знаменатель на число, сопряженное знаменателю: |
|
|||||||||||||||||
|
x + iy |
|
|
(x + iy )(x −iy |
) |
|
x x + y y |
2 |
+i( y x − x y |
) |
|
x x |
+ y y |
|
||||
|
1 |
1 |
= |
1 |
1 |
2 |
2 |
|
= |
1 2 1 |
1 2 1 2 |
|
= |
1 2 |
1 |
2 |
||
|
x + iy |
2 |
(x + iy |
)(x −iy |
) |
x2 |
−i2 y2 |
|
x2 |
+ y2 |
|
|||||||
|
|
|
|
|
|
|||||||||||||
2 |
|
|
2 |
2 |
2 |
2 |
|
|
|
2 |
2 |
|
|
2 |
2 |
|
||
|
z |
|
|
Это число и берется за определение частного |
|
1 |
. |
z |
|
||
|
2 |
|
|
|
|
|
|
+i y1x2 − x1 y2
x2 + y2
2 2
.
Легко проверить, что введенные действия обладают обычными свойствами аналогичных действий над действительными числами. Отметим также, что
|
|
|
|
|
|
|
|
|
|
|
|
|
___ |
|
z |
|
||
_________ |
|
|
|
|
_____ |
|
|
|
|
z |
|
|
||||||
1) z |
z |
|
= z |
z |
|
. |
2) z z |
|
= z z |
|
. |
3) |
|
1 |
= |
|
1 |
. |
2 |
2 |
2 |
2 |
|
|
|
|
|||||||||||
1 |
|
1 |
|
|
1 |
1 |
|
|
z |
|
|
z |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Неравенств для комплексных чисел нет.
Геометрическое изображение комплексных чисел.
Сопоставив комплексному числу z = x + iy точку плоскости 0ху с координатами (х, у), мы получим взаимно однозначное соответствие между комплексными числами и точками плоскости 0ху , которую мы будем при этом называть комплексной плоскостью, а произвольную точку (х, у) обозначать также числом z = x + iy.
Определение 9. Полярные координаты r и точки (х, у) называются соответственно модулем и аргументом комплексного числа z = x + iy и обозначаются r =| z |, = Arg z .
На рис. 2 угол определяется с точностью до целого кратного 2 π . Единственное значение аргумента, принадлежащее промежутку (−π, π , называется главным значением аргумента
|
arg z |
|
|
2 |
|
2 |
|
y |
|
x |
|
y |
(arg z находится по |
|
|
|
|
|
|
|
|
|
|
|
|
||
и обозначается |
. | z |= |
x |
|
+ y |
|
и sin = | z | |
, cos = | z | , tg = x |
||||||
|
|
|
|||||||||||
любой из этих трех формул с учетом четверти комплексной плоскости, в которой лежит z). Если же z = 0, то r = 0 , а = Arg z – любой.
8
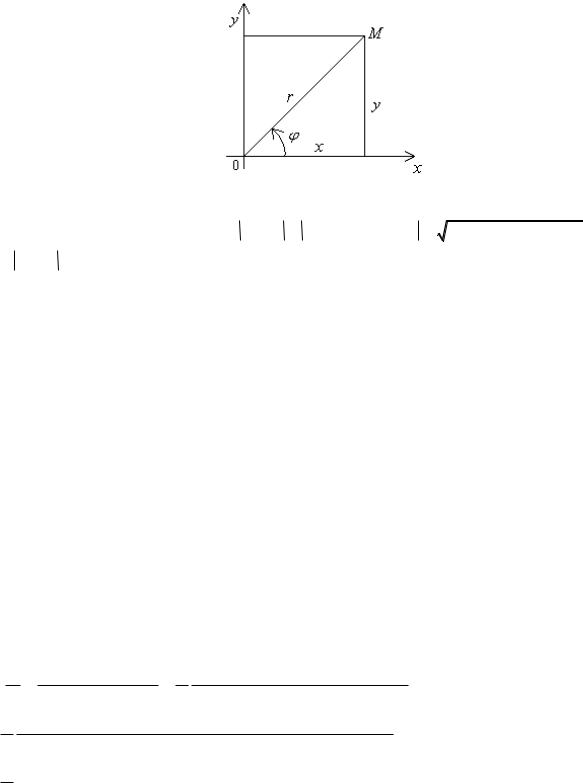
Рисунок 2
Если
z |
= x +iy , |
|
1 |
1 |
1 |
z |
= x |
+iy |
, |
2 |
2 |
2 |
|
то
z |
2 |
− z |
= x |
− x |
+ i( y |
2 |
− y ) |
|
1 |
2 |
1 |
|
1 |
= |
(x |
− x ) |
2 |
+ ( y |
|
− y ) |
2 |
, |
|
2 |
|
||||||
|
2 |
1 |
|
|
1 |
|
|
т.е. |
z |
2 |
− z |
– это расстояние на комплексной плоскости между точками |
(x , |
|
1 |
1 |
или между точками z1 = x1 +iy1 и z2 = x2 +iy2 .
Тригонометрическая форма комплексного числа
y1)
и
(x |
2 |
, |
|
|
y |
2 |
) |
|
|
,
Из рис. 2 видно, что для комплексного числа z = x + iy |
x = r cos , |
y = r sin |
z = r(cos +i sin ). |
|
|
Определение 10. Форма записи (2) называется тригонометрической формой комплексного числа.
(2)
Действия над комплексными числами в тригонометрической форме
Пусть
z |
= r (cosφ +i sin φ ), |
||
1 |
1 |
1 |
1 |
z |
= r (cosφ |
2 |
+i sin φ |
). |
2 |
2 |
2 |
|
Тогда:
z z |
= r r (cos φ +i sin φ )(cosφ |
2 |
+i sin |
φ |
) = |
|
|
|
|
|||||||
а) |
1 |
2 |
1 2 |
|
1 |
1 |
|
|
|
2 |
|
|
|
|
|
|
= r r |
cos φ cos φ |
2 |
−sin φ sin φ |
2 |
+ i(sin φ |
cos φ |
2 |
+ cos φ sin φ |
2 |
) = |
||||||
1 |
2 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
||||
= r1r2 cos(φ1 |
+ φ2 ) + i sin(φ1 + φ2 ) |
, т.е. |
при |
умножении |
комплексных чисел их модули |
|||||||||||
перемножаются, а аргументы складываются;
б)
=
z |
= |
r (cos φ |
+i sin φ ) |
= |
r |
|
|
(cos φ |
|
+i sin φ )(cos φ |
|
|
−i sin φ |
) |
= |
|||||||||||||||
|
1 |
1 |
1 |
|
1 |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
2 |
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
z |
2 |
|
r (cos φ |
2 |
+i sin φ |
) |
|
r |
|
(cos φ |
2 |
+i sin φ |
|
)(cos φ |
2 |
−i sin φ |
) |
|
||||||||||||
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||
r |
(cos φ cos φ |
|
+sin φ sin φ |
|
) + i(sin φ cos φ |
|
|
−cos φ sin φ |
) |
= |
|
|||||||||||||||||||
1 |
|
|
1 |
|
2 |
1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
2 |
|
|
|
1 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
r |
|
|
|
|
|
|
cos |
2 |
φ |
|
+ sin |
2 |
φ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= r1 [cos(φ2 − φ1 ) + i sin(φ2 − φ1 )], т.е. при делении комплексных чисел их модули делятся, а r2
аргументы вычитаются;
в) из свойства а) следует, что если z = r(cos φ +i sin φ), то
zn = r(cos φ +i sin φ) r(cosφ +i sin φ) ... r(cosφ +isin φ) = rn (cos nφ +i sin nφ) ,
т.е. при возведении комплексного числа в натуральную степень его модуль возводится в эту степень, а аргумент умножается на эту степень;
9
