
вышмат полезно
.pdf
Решение. По формуле тройного аргумента cos3x 4cos3 x 3cosx . Выразим отсюда куб косинуса и проинтегрируем почленно по формуле 22.3.5:
cos3 xdx 3cosx cos3x dx |
3sinx |
1 |
sin3x |
C |
9sinx sin3x |
C |
4 |
4 |
4 |
3 |
|
12 |
|
22.4.7. Найдите sin(2x 3)dx .
Решение. По формуле синуса суммы, свойству линейности 22.2.1 и табличным интегралам 22.3.4, 22.3.5 получим
sin(2x 3)dx (sin2x cos3 cos2x sin3)dx cos3 sin2xdx
sin3 cos2xdx cos3 cos22 x sin3 sin22 x C 12cos(2x 3) C .
22.4.8. Вычислите tg2 xdx .
Решение.
tg |
2 |
xdx |
sin2 xdx |
|
1 cos2 x |
dx |
dx |
1 dx tgx x C . Здесь мы |
|
cos2 x |
cos2 x |
cos2 x |
воспользовались интегралами 22.3.8 и 22.3.1 (при 0).
22.4.9. Вычислите 2xdx2 3.
|
|
Решение. Вычисление по формуле 22.3.12 (a2 |
3 |
, т. е. a |
3/ 2 ). |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
1 |
|
|
dx |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
C |
|
|
|
|
|
arctg x |
|
|
C . |
||||||||||
|
|
|
2x2 |
3 |
2 |
x2 |
3/ 2 |
2 |
3/ 2 |
|
3/ 2 |
|
6 |
3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
22.4.10. Найдите |
|
2 |
|
x2 1 |
|
x2 |
1 |
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x4 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Решение. Представим знаменатель в виде |
x4 1 |
|
|
x2 1 |
x2 1: |
|||||||||||||||||||||||||||||||||||||||||||
|
2 x2 1 |
x2 1 |
dx |
2 |
|
|
dx |
|
|
|
|
dx |
|
|
2ln |
|
x x |
2 |
1 |
|
ln |
|
x |
x |
2 |
1 |
|
C . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
x |
2 |
1 x |
2 |
1 |
|
|
x |
2 |
|
1 |
|
x |
2 |
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Применили свойство линейности 22.2.1 и табличный интеграл 22.3.15 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
22.4.11. Вычислите |
|
|
|
|
|
|
|
x2dx |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
1 x |
2 |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
121 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
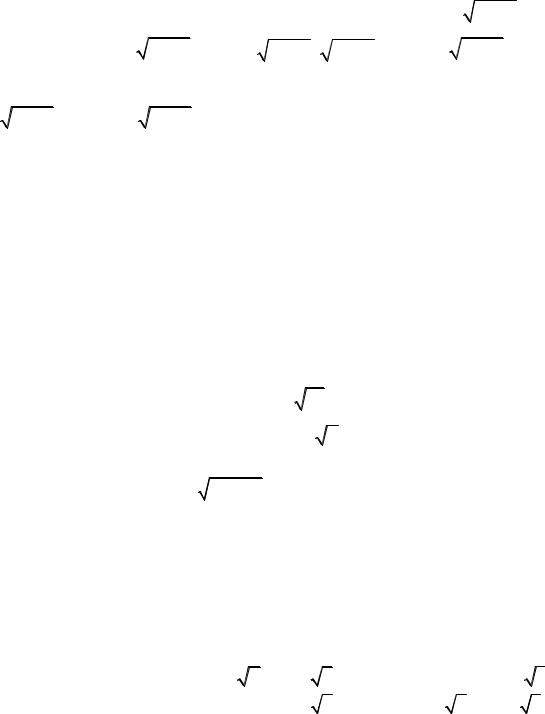
|
Решение. |
|
x2dx |
|
|
x2dx |
|
|
x2 1 x2 1 dx |
|
|||
|
1 |
1 x2 |
x2 |
1 x2 1 x2 |
1 |
1 x2 ( x2) |
|||||||
|
1 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
1 dx |
|
|
dx arcsinx x C . Здесь мы умножили на |
||||||||
1 x |
2 |
1 x |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
сопряженное выражение и воспользовались табличным интегралом 22.3.13.
22.4.12. Найдите sh2 5xdx .
Решение. Многие формулы для гиперболических функций похожи на формулы тригонометрии. Например, понижение степени: sh2 ch22 1.
Отсюда sh2 5xdx |
1 |
ch10x 1 dx sh10x |
x |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22.5. Задачи для самостоятельного решения |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
22.5.1. x(x 1)(x 2)dx . |
22.5.2. |
5 |
x2 2 2 |
dx . 22.5.3. |
2x2 1 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx . |
||||||||||||||||||||||||||||
|
3 x |
|
|
|
x2 x4 |
||||||||||||||||||||||||||||||||||
22.5.4. |
x2 3 |
|
22.5.5. |
|
dx |
|
|
|
22.5.6. |
3 2x 2 3x |
dx . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
dx . |
|
|
|
|
. |
|
|
|
6x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x2 2 |
|
3 5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
22.5.7. sin2 2xdx . |
|
|
22.5.8. sin3 3xdx . |
|
|
22.5.9. |
|
cos2x |
|
|
dx . |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
cos2 x sin2 x |
|
|
|
||||||||||||||||||||||||||||||||
22.5.10. th2 2xdx . |
|
|
22.5.11. cos2x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sinx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответы. |
22.5.1. |
|
x4 |
x3 |
|
|
2 |
C . 22.5.2. |
15 |
|
22/15 |
6x |
2/3 |
15 |
16/15 |
|
C . |
||||||||||||||||||||||
|
|
|
|
x |
|
|
22 x |
|
|
|
4 |
x |
|
||||||||||||||||||||||||||
|
4 |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
22.5.3. arctgx |
1 C . 22.5.4. x 5 |
2 ln |
|
x |
2 |
|
|
C . 22.5.5. |
|
1 |
arcsin |
x |
5 |
C . |
|||||||||||||||||||||||||
|
x |
2 |
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
||||
22.5.6. 2 2 x |
3 3 x |
C . 22.5.7. |
x |
sin4x |
C |
. 22.5.8. |
cos9x |
cos3x C . |
|||||||||||||||||||||||||||||||
ln3 |
|
36 |
|
|
|||||||||||||||||||||||||||||||||||
ln2 |
|
|
|
|
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||||||
22.5.9. ctgx tgx C . |
|
22.5.10. x th2x C . |
|
|
x |
|
|
||||||||||||||||||||||||||||||||
|
|
22.5.11. 2cosx ln |
tg |
|
C . |
||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
ЗАНЯТИЕ 23 23. ВНЕСЕНИЕ ПОД ЗНАК ДИФФЕРЕНЦИАЛА.
ИНТЕГРИРОВАНИЕ МЕТОДОМ ПОДСТАНОВКИ
122

Дальнейшее развитие техники интегрирования основано на применении замены переменной, т.е. свойства 22.2.2 и, в частности, 22.2.3. Метод замены переменной допускает два подхода, различающиеся лишь внешне.
23.1. Внесение под знак дифференциала
Вычисление неопределенного интеграла не сводится к интегрированию отдельных множителей подынтегральной функции! Однако в не-
которых случаях множитель можно внести под знак дифференциала, пользуясь свойством 22.2.5 (см. также дифференциалы в 22.3.1–22.3.11) и далее сделать замену переменной по свойству 22.2.2. Например:
f (cosx)sinxdx f (t)dt , где t cosx ; f (xn )xn 1dx 1n f (t)dt , где t xn .
23.2. Решение некоторых типовых примеров на внесение под знак дифференциала
23.2.1. Вычислите xx4dx1.
Решение. По 22.3.1 |
|
x |
2 |
|
|
1d (x2) |
|
xdx |
|
1 d(x2) |
|
|||||||||
xdx d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
x |
4 |
1 |
2 (x |
2 |
) |
2 |
1 |
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
1dt 1 1
2 t2 1 2arctgt C 2arctgx2 C . Здесь t x2.
23.2.2.Найдите tg3 xdx .
|
|
Решение. Перепишем ответ к примеру 22.4.8 в виде tg2 xdx d(tgx x) |
||||
, |
|
|
|
|
|
тогда |
tg3 |
xdx tgx tg2 xdx tgxd(tgx x) tgxd(tgx) tgxdx tdt ln|cosx | |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
tgx t |
22.3.18 |
|
|
|
|
|
|
|
|
t2 |
ln|cosx | C |
tg2 |
x |
ln|cosx | C . |
|
2 |
2 |
|
|
|||
|
|
|
|
|
||
23.2.3. Найдите cos5 3xdx .
Решение. Согласно 22.3.5 cos3xdx 13d(sin3x). Внесем косинус под
знак дифференциала; четвертую степень косинуса выразим, пользуясь тождеством «тригонометрическая единица»: cos4 3x (1 sin2 3x)2 . Тогда
|
cos5 3xdx 1 |
|
cos4 |
3xd (sin3x) |
1 |
1 sin2 3x |
|
2 d ( |
sin3x |
) 1 |
|
(1 t2)2 dt |
||||||||
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначим t |
|
|
||||
|
1 |
(1 2t2 |
t4 )dt |
t |
|
2t3 |
|
t5 |
C sin3x |
2sin3 3x |
sin5 3x C . Таким же |
|||||||||
3 |
|
9 |
|
|||||||||||||||||
|
|
|
|
|
3 |
|
15 |
|
3 |
|
|
9 |
15 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
123 |
|
|
|
|
|
|
|
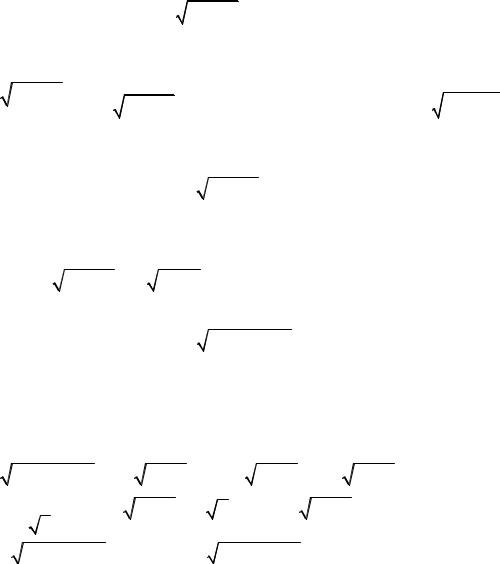
способом можно было решить пример 22.4.6, при этом ответы выглядели бы по-разному, но при помощи формул тригонометрии легко установить их тождественность.
|
|
23.2.4. Вычислите |
|
dx |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x ln3 2x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Решение. По 22.3.2 dx d(ln| x |). В этом примере в область определе- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
ния входят лишь x 0 |
| x | x . Дифференциал не меняется, если под его |
|||||||||||||||||||||||||||||
знаком прибавить любую константу, поэтому |
dx d(lnx ln2) d(ln2x). |
|||||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
d (ln2x) |
dt |
t 2 |
1 |
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Итак, |
|
|
|
|
ln3 2x |
|
|
|
|
|
t3 |
2 |
|
|
C . Здесь t ln2x . |
|||||||||||||||
x ln3 2x |
|
|
|
|
|
2ln2 2x |
||||||||||||||||||||||||
|
|
23.2.5. Найдите |
|
arctgx |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
arctgx |
dx |
|
|
arctgxd(arctgx ) |
|
t1/2dt |
t3/2 |
C 2 arctg3 x C . |
|||||||||||||||||||||
|
|
3/ 2 |
||||||||||||||||||||||||||||
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначим t |
|
|
|
|
|
|
|
|
|
||||||||
|
|
23.2.6. Вычислите |
|
|
|
exdx |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 e |
|
|
|
|
|
|
|
|
|
|||
|
|
Решение. Согласно свойству 22.2.5 и 22.3.3 |
exdx d(ex ). Пусть ex t , |
|||||||||||||||||||||||||||
тогда |
|
|
exdx |
|
|
dt |
|
|
|
|
arcsin |
t |
|
C arcsin ex |
C . |
|||||||||||||||
|
2x |
|
4 t |
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
4 e |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|||||
|
|
23.2.7. Вычислите |
|
|
|
(3x 1)dx |
|
. |
|
|
|
|
||||||||||||||||||
|
|
|
x2 4x 7 |
|
|
|
|
|||||||||||||||||||||||
Решение. Выделим в подкоренном выражении полный квадрат:
x2 4x 7 (x 2)2 3. |
Представим числитель |
3x 1 3(x 2) 5. |
Обозна- |
||||||||||||||||||||||||
чим |
|
|
|
|
|
|
|
x 2 t , |
|
|
|
d(t2 |
тогда |
|
|
|
|
dx dt |
и |
||||||||
|
(3x 1)dx |
|
|
|
(3t 5)dt |
|
3 |
|
3) |
5 |
|
|
dt |
|
|
|
|||||||||||
|
x |
2 |
4x |
7 |
|
t |
2 |
|
3 |
2 |
t |
2 |
3 |
|
t |
2 |
|
|
|
||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||
|
|
|
dz |
|
t2 3 |
|
|
|
t2 3 |
|
|
||||||||||||||||
|
|
5ln |
t |
3 |
z 5ln |
t |
C |
|
|||||||||||||||||||
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C . Здесь z t2 3 x2 4x 7. |
||||||||||
3 |
|
x2 4x 7 5ln |
x 2 |
x2 4x 7 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23.3. Интегрирование методом подстановки
124

Метод подстановки основан на свойстве 22.2.2. В самом начале решения выбирается подходящая замена x (t), где (t) — дифференцируемая
функция. Переписывая интеграл, в обязательном порядке пересчитывают дифференциал по формуле dx (t)dt . Выделим несколько полезных подста-
новок:
23.3.1.f (n x)dx n f (t)tn 1dt ; подстановка x tn , t x1/n , dx ntn 1dt .
23.3.2.f (ex )dx f (tt)dt ; подстановка t ex , x lnt , dx dtt .
23.3.3.f ( a2 x2 , x)dx a f (a cost, asint)costdt ;
|
подстановка x asint , t arcsin |
x |
, dx a costdt , |
|
|
|
a2 x2 |
a cost . |
||||||||||||||||||||||||||||
|
a |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
23.3.4. |
|
f ( |
a |
2 |
x |
2 |
, x)dx a |
|
|
f |
|
a |
, |
a tgt |
|
|
dt |
|
|
|
; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
t |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cost |
|
|
|
|
cos |
|
|
|
|
|
|
|
||||||||||||
|
подстановка x a tgt , t arctg |
|
x |
, |
|
|
dx |
|
adt |
, |
|
a2 x2 |
|
|
a |
. |
||||||||||||||||||||
|
|
a |
|
|
cos2 t |
|
cost |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
23.3.5. |
f ( |
|
2 |
|
2 |
, x)dx a |
|
|
|
|
|
|
a |
|
|
sintdt |
|
|
|
|
|
||||||||||||||
|
x |
|
a |
|
f a tgt, |
|
|
|
|
|
|
|
|
2 |
|
; |
подстановка |
|||||||||||||||||||
|
|
|
|
cost |
|
|
|
t |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|||||||||||
x |
a |
, |
t arccosa , |
|
dx |
asintdt |
|
, |
|
|
x2 a2 |
a tgt |
|
|
(" "при x 0, |
|||||||||||||||||||||
cost |
|
cos2 t |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
" "при x 0).
Часто применяется линейная подстановка (см. свойство 22.2.3).
23.4. Решение некоторых типовых примеров на метод подстановки
23.4.1. Найдите x x1dx .
|
|
Решение. В соответствии с 23.3.1 запишем: t |
x , x t2, dx 2tdt , |
|||||||||
|
|
x |
t |
|
(t2 1) 1 |
|
dt |
|
||||
|
|
dx |
|
|
|
2tdt |
2 |
t2 1 |
dt 2 dt 2 |
|
2t 2arctgt C |
|
x 1 |
t2 |
|
1 |
t2 1 |
||||||||
2 |
x 2arctg |
x C . |
|
|
|
|
|
|||||
23.4.2. Найдите exdx 1.
125
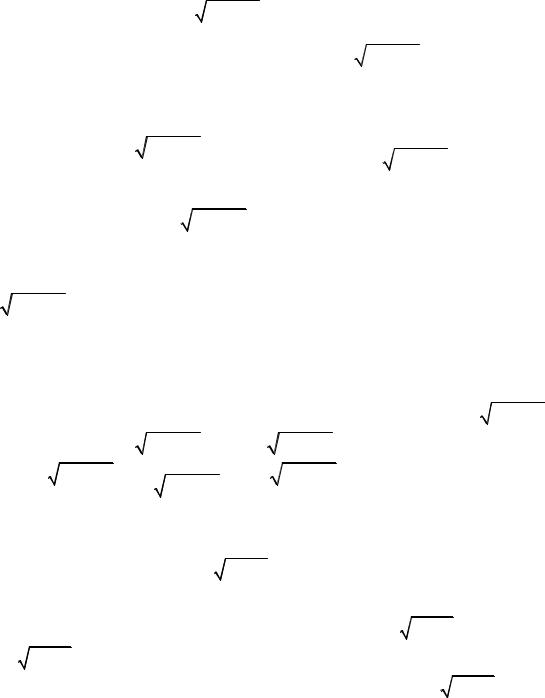
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подстановка 23.3.2. Получим |
|
|
dx |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
x |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
, где t e |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ex |
1 |
|
t(t 1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дробь |
|
|
|
1 |
|
|
|
|
представим в виде: |
|
|
|
|
1 |
|
|
(t 1) t |
|
1 |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
t(t |
1) |
|
t(t 1) |
|
t(t 1) |
|
|
t |
t |
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Тогда |
|
|
|
|
|
dt |
|
|
|
|
|
dt |
|
|
dt |
ln|t | ln |t 1| C x ln(e |
x |
1) C . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t(t 1) |
|
|
|
|
t |
|
t 1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
23.4.3. Вычислите |
|
|
|
a2 x2dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Решение. Случай подстановки 23.3.3. |
|
|
|
a2 |
x2dx a2 cos2 tdt |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a2 |
(1 cos2t)dt |
a2 |
|
|
|
|
|
|
sin2t |
|
|
|
|
|
|
a2 |
t sint cost C |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 t |
|
|
|
2 |
|
|
C |
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
2 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
a |
2 |
x |
2 |
|
|
|
|
a |
2 |
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
a2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
arcsin |
|
|
|
|
|
|
|
|
|
|
|
C |
|
arcsin |
|
|
|
|
|
C . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23.4.4. Найдите |
|
|
|
|
|
|
|
|
x2 a2 |
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
Решение. |
Пример на подстановку 23.3.4. Перепишем интеграл через t : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x2 a |
2 |
|
|
|
|
|
|
|
|
|
a /cost |
|
|
|
|
adt |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
sin2 t cos2 t |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
a tgt |
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
sint cos2 t |
|
|
dt |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
cos2 t |
sint cos2 t |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
sintdt |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
d(cost) |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
a cos2 t a |
|
|
|
a |
|
|
|
cos2 t |
|
a ln |
tg |
|
|
|
|
|
|
|
|
|
|
a ln |
tg |
|
|
|
C . Возвра- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sint |
|
|
|
|
2 |
cost |
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тимся к x : |
|
cost |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
, sint |
|
|
x |
|
|
|
|
|
, |
|
tg |
t |
|
|
|
1 cost |
|
|
|
|
|
|
x2 a2 a |
, |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x2 a |
2 |
|
|
|
x2 a2 |
|
|
2 |
|
|
|
sint |
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
тогда |
|
|
|
|
x2 |
a2 |
dx |
|
|
|
x2 a2 aln |
|
x2 a2 a |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
23.4.5. Вычислите |
|
|
|
|
dx |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Решение. Выберем подстановку 23.3.5: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
cos2 t |
sintdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
tgt |
cos2 t |
|
costdt sint C |
|
|
|
|
|
|
|
|
C . Для записи |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x2 |
x2 1 |
|
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ответа через переменную |
|
|
x выразили sint tgt cost |
|
|
x2 1 |
. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
126

Замечание. При использовании подстановки 23.3.5 следует учитывать знак переменной интегрирования. Здесь результат не зависит от знака; следующий пример демонстрирует обратную ситуацию.
|
|
|
23.4.6. Найдите |
|
|
|
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
x |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Решение. Как и в примере 23.4.5 сделаем подстановку |
x |
1 |
|
|
|
|
, полу- |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
cost |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
cost sintdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
чим |
|
|
|
|
|
|
|
|
tgt cos2 t |
dt t C arccos x |
|
C . Для x 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|
x2 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
выбирается знак " "; |
для x 1 – знак " ". |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
23.4.7. Найдите |
|
dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
sh2(3x 4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно 22.3.11 |
|
|
и 22.2.3 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
3cth(3x 4) C . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
sh2(3x 4) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
23.4.8. Вычислите |
|
|
|
x2dx |
|
|
|
. Решение. Сделаем замену t 2x 1, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(2x 1)5 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тогда x |
t 1 |
|
и |
dx dt |
|
|
, тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
dx |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
1 |
|
t |
2 |
2t |
1 |
|
1 |
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t5 |
|
|
|
|
|
|
|
8 |
|
|
|
|
t5 |
|
|
|
|
|
|
dt |
8 t |
|
|
dt 2 t |
|
|
|
|
dt |
t |
|
|
dt |
|
|
|
|
|
|||||||||||||||||||||||||||
(2x 1)5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
t |
|
|
|
|
|
2t |
|
|
t |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C . |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
8 |
|
|
|
|
|
|
|
|
16(2x 1) |
2 |
|
12(2x 1) |
3 |
|
|
|
32(2x 1) |
4 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23.5. Задачи для самостоятельного решения |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
23.5.1. |
|
|
|
|
|
|
|
x |
|
|
4 dx . |
|
|
|
23.5.2. |
|
|
|
|
|
cosxdx |
. |
|
|
|
23.5.3. |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
. |
|
|
23.5.4. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xlnx lnlnx |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
cos |
1 dx . |
|
|
|
|
|
|
|
23.5.5. |
|
|
|
|
sin |
|
|
|
x dx |
. 23.5.6. |
|
|
xdx |
|
|
|
|
|
. 23.5.7. sin3 xdx . |
|||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ch |
2 2 |
|
1) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosx |
||||||||||||||||
23.5.8. |
arccos2 2x |
dx |
. |
|
|
|
23.5.9. |
|
|
|
|
arctg |
x |
dx . |
|
|
|
|
23.5.10. |
sh x ch3 x |
dx . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 4x |
2 |
|
|
|
|
|
(1 x) x |
|
|
|
|
1 ch |
2 |
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
exdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
23.5.11. |
|
|
|
. |
|
|
|
23.5.12. |
|
x2 a2dx . |
|
23.5.13. |
|
|
|
|
|
|
|
|
dx |
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
e |
x |
|
1 |
|
|
|
|
|
|
|
(1 x |
2 |
) |
1 x |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
127

23.5.14. |
|
|
x2 1 |
|
dx . |
|
|
|
23.5.15. |
|
|
|
|
dx |
|
|
|
. |
|
|
|
|
|
|
23.5.16. |
|
|
dx |
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
cos(5x 2) |
|
||||||||||
23.5.17. |
|
|
|
xdx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответы. |
23.5.1. |
|
1 |
|
|
|
|
|
C . |
|
23.5.2. arcsin(sinx |
2) C . |
|
|
|
|||||||||||||||||||||||||||||||||
15(x5 1)3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
23.5.3. lnlnln x C . 23.5.4. sin |
1x |
C . 23.5.5. 2cos |
|
|
x C |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
. 23.5.6. |
|
1 |
th(x2 1) C . |
23.5.7. |
|
2 |
(cosx)5/2 |
2 |
|
cosx C . 23.5.8. 1arccos3 2x C |
||||||||||||||||||||||||||||||||||||||
|
|
5 |
|
|||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
||||||
. 23.5.9. arctg2 |
x C |
. |
|
23.5.10. |
ch2 |
x ln(1 ch2 |
x) |
C . |
23.5.11.2 |
ex 1 C . |
||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||
23.5.12. |
x |
|
|
x2 a2 |
|
a2 |
|
|
|
|
x2 |
a2 |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
23.5.13. |
|
|
|
C |
||||||||||||||||||
|
|
|
ln |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
. |
|
|
|
|
|
|
|
23.5.14. |
|
x2 1 arccos |
1 |
C . |
|
|
|
|
|
|
|
|
|
23.5.15. |
|
|
1 x2 |
|
C |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
. 23.5.16. |
|
|
|
|
|
|
|
|
. 23.5.17. |
|
|
(2x |
3) |
3 |
|
|
2x 3 C . |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
ln |
tg |
|
|
|
1 |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
5 |
|
2 |
|
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ЗАНЯТИЕ 24
24.МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
24.1.Описание метода интегрирования по частям
Метод интегрирования по частям основан на формуле, выведенной в 22.2.6: u(x)v (x)dx u(x) v(x) v(x)u (x)dx . Эту формулу можно приме-
нять к любым дифференцируемым функциям u(x) и v(x), но не всегда новый
интеграл вычисляется проще исходного. Приведем основные случаи, когда способ интегрирования по частям позволяет найти исходный интеграл.
Исходный интеграл udv u(x) v (x)dx .
24.1.1.u(x) xn , n N ; v (x) sin(kx b) или v (x) cos(kx b).
24.1.2.u(x) xn , n N ; v (x) akx .
24.1.3.u(x) logna (kx b), где n N ; v (x) – рациональная или иррациональная функция, у которой первообразная v(x) также рациональна или иррациональна.
128

24.1.4. u(x) – натуральная степень обратной тригонометрической функ-
ции (например, u(x) arcsin |
n |
kx , u(x) arctg |
|
|
x и т. п.); v (x) – рациональная |
или иррациональная функция с известной рациональной или иррациональной первообразной v(x).
Порядокинтегрированияпочастямследующий:1)определяемфункцию u(x); 2) находим v(x) по формуле v(x) v (x)dx , при этом произвольную
постоянную интегрирования выбираем равной нулю; 3) вычисляем диф-
ференциал du u (x)dx ; 4)применяемформулу udv uv vdu .Принеобходимости применяем к полученному интегралу vdu v(x)u (x)dx формулу интегрирования по частям повторно.
24.2. Рекуррентная формула для интеграла |
dx |
|
|
(x2 a2)n 1 |
|
Неопределенные интегралы, к которым применим метод интегрирования по частям, не исчерпываются основными случаями, указанными в 24.1.1–
24.1.4. Выведем рекуррентную формулу для интеграла |
|
In |
|
|
|
dx |
|
|
, поло- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(x2 |
a2)n |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v dv dx x , |
|
|
|
|
|
|
|
|
|
|
|
|
n 2xdx |
||||||||||||||||||||||||||||||||
жив u |
|
|
|
|
|
|
|
|
|
|
, |
|
dv dx , |
du u dx |
|
|
|
|
|
|
|
|
|
|
|
. По |
||||||||||||||||||||||||||||||||||||||||||||
(x |
2 |
a |
2 |
) |
n |
|
(x |
2 |
a |
2 |
) |
n 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
формуле 22.2.6 |
|
|
|
|
|
|
|
x2dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 a2) a2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
In |
|
|
|
x |
|
|
2n |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2n |
dx |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
(x2 a2)n |
(x2 a2)n 1 |
(x2 a2)n |
(x2 a2)n 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2nIn 2na2In 1 . |
||||||||||||||||||||||
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
(x |
2 |
|
2 |
) |
n |
(x |
2 |
|
|
2 |
) |
n |
|
|
|
(x |
2 |
a |
2 |
) |
n 1 |
(x |
2 |
a |
2 |
) |
n |
|||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Выразим теперь из этого равенства In 1: |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
In 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n 1)In . |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
a |
2 |
) |
n |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2na |
(x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
C (табличный интеграл 22.3.12). Таким |
||||||||||||||||||||||||||||||||||||||||||||||||||
Очевидно, |
|
|
|
|
a arctg |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x2 |
a2 |
a |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
образом, можно последовательно найти I2 , |
I3 |
|
и т. д. по формуле |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n 1) |
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(x |
2 |
2 |
) |
n 1 |
|
2na |
2 |
|
2 |
a |
2 |
) |
n |
|
|
(x |
2 |
2 |
) |
n |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
(x |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||||||||||||||||||||||||||||||||||
24.3. Решение некоторых типовых задач, рассматриваемых в аудитории
24.3.1. Вычислите (2x 1)sinxdx .
129

Решение. Случай 24.1.1 |
u 2x 1, |
du (2x 1) dx 2dx, |
dv sinxdx , |
|
|
|
|
|
|
v sin xdx cosx , |
тогда |
(2x 1)sinxdx (2x 1)cosx 2 cosxdx |
||
(2x 1)cosx 2sinx C .
24.3.2.Найдите x2e 2xdx .
|
Решение. Случай 24.1.2. |
Выберем u x |
2 |
, |
|
|
|
dv e |
2x |
dx , |
||||||||||||||||||
|
|
du u dx 2xdx , |
|
|||||||||||||||||||||||||
|
|
|
2x |
|
|
|
|
|
|
|
|
x |
2 |
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
v e 2xdx e2 |
|
; x2e 2xdx |
|
e |
|
xe 2xdx . К вновь полученному инте- |
||||||||||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||||||
гралу применим |
интегрирование |
|
по |
|
частям |
|
|
повторно; |
на этот |
раз u x , |
||||||||||||||||||
du dx , а v не меняется. Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
xe 2xdx xe 2x |
e 2x dx xe 2x |
e 2x C . В итоге |
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||
x2e 2xdx |
x2e 2x |
|
xe 2x |
e 2x |
C 1 2x2 |
2x 1 e 2x C . |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
|
2 |
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||
|
24.3.3. Найдите |
x lnxdx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Решение. |
Случай |
|
24.1.3. |
|
|
Примем |
|
u(x) lnx , |
|
|
dx |
dx |
|||||||||||||||
|
|
|
|
|
du (lnx) |
x , |
||||||||||||||||||||||
|
xdx dv , |
v |
|
|
xdx |
2x |
x |
. |
|
По |
формуле |
|
интегрирования |
по |
частям |
|||||||||||||
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x lnxdx |
2x x lnx 2x |
x |
dx |
2x x lnx |
2 |
xdx |
2x x lnx |
4x |
x C |
||||||||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
|
|
x |
|
|
|
3 |
|
|
|
3 |
|
3 |
|
|
9 |
|
||
24.3.4. Вычислите x arctgxdx .
Решение. |
Примем, как указано в 24.1.4, u arctgx . Тогда |
xdx dv , |
||||||||||
v xdx |
x2 |
du arctgx dx |
dx |
|
|
x2 |
x2 |
|
dx |
|||
|
, |
|
; |
x arctgxdx |
|
arctgx |
|
|
|
. |
||
2 |
x2 1 |
2 |
2 |
x2 1 |
||||||||
Последний интеграл найдем, выделив целую часть подынтегральной дроби:
|
x2 |
|
|
dx |
|
|
|
1 |
x2 1 1 |
|
1 |
|
|
|
|
1 |
|
|
1 |
x arctgx C . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
dx |
|
|
1 |
|
|
|
|
|
dx |
|
|
В итоге |
|||
2 |
x |
2 |
1 |
x |
1 |
|
2 |
x |
2 |
1 |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
получим |
x arctgxdx |
x2 |
arctgx |
1 x |
1arctgx C |
x2 1 |
arctgx |
x |
C . |
|||||||||||||||||||||
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
||||
|
|
|
24.3.5. Вычислите arcsin |
xdx . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
|
||
