
вышмат полезно
.pdf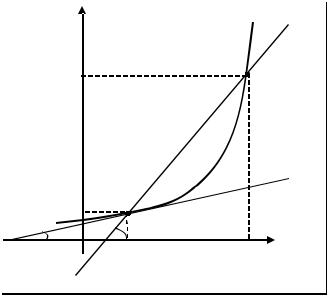
Ответы. 6.3.1. x 0 устранимый разрыв; 6.3.2. x 0 разрыв 2-го рода; 6.3.3. x 0 устранимый разрыв, x 1 разрыв 2-го рода; 6.3.4. x 0 разрыв 1-го рода; 6.3.5. x 0 разрыв 1-го рода; 6.3.6. x 1 разрыв
2-го рода; 6.3.7. x 3 устранимый разрыв, |
x 3 разрыв 2-го рода; 6.3.8. |
x 0 и x 1 разрывы 1-го рода. |
|
ЗАНЯТИЕ 7.
7.ПРОИЗВОДНЫЕ ПЕРВОГО ПОРЯДКА
7.1.Вычисление производных. Производная сложной функции
Определение 7.1.1. Производной функции |
y f (x) в точке |
x0 называется |
|||||||||
число |
|
f (x) = lim |
f (x0 x) f (x0) |
|
f (x) f (x0) |
|
|||||
y (x0) f (x0) lim |
= lim |
, |
|||||||||
|
|
|
|||||||||
|
x 0 |
x |
x 0 |
|
x |
|
x x0 |
x x0 |
|||
|
|
|
|
|
|
|
|||||
если этот предел существует и конечен (если предел бесконечен, то иногда |
|||||||||||
говорят про бесконечную производную). |
|
|
|
|
|
||||||
Обозначение: |
f (x0) lim |
f (x) f (x0) |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
x x0 |
x x0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Разность |
x x x0 |
называется |
приращением |
аргумента, а |
|||||||
y f (x) f (x0) приращением функции. Таким образом, можно опреде-
лить производную как y lim y .
x 0 x
Геометрический смысл производной
у
|
|
В |
Dу |
|
|
|
А |
|
a0 |
a |
х |
|
х0 |
х0+D |
Рис. 7.1 51

Рассмотрим график функции y f (x) и проведем секущую через точки A с абсциссой x0 и B с абсциссой x0 x . Если обозначить разность ординат этих точек y , то тангенс угла , образованного секущей с осью Ох, можно
представить так: tg yx .
Если x 0, точка B перемещается по кривой, приближаясь к точке A
, и секущая при совпадении точек B и A превращается в касательную к графику функции, образующую с осью Ох угол 0 .
При этом tg 0 lim y f (x0).
x 0 x
Значение производной при данном значении x равно тангенсу угла, обра-
зованного касательной к графику функции в точке с соответствующим значением x с положительным направлением оси Ох.
Механический смысл производной
Рассмотрим прямолинейное движение тела, для которого пройденное расстояние есть функция от времени: s f t . Среднюю скорость за время t
можно определить по формуле: vcp st .
Для определения мгновенной скорости тела в данный момент времени
устремим t |
к нулю. Получим: v lim |
s |
lim |
s(t0 t) s(t0) |
s (t0). |
t |
|
||||
|
t 0 |
t t0 |
(t0 t) t0 |
||
|
|
|
|
||
Таким образом, производная от расстояния в данный момент времени равна мгновенной скорости движения в этот момент. Соответст-
венно,
Производная любой функции при данном значении аргумента равна скорости изменения этой функции при рассматриваемом x .
Необходимое условие существования производной |
|
Теорема 7.1.1. Пусть функция y f (x) имеет в точке x0 производную |
f (x0) |
. Тогда эта функция непрерывна в точке x0 . |
|
Основные правила дифференцирования |
|
Теорема 7.1.2. Пусть в некоторой точке существуют производные u x и v x , тогда в этой точке справедливы следующие равенства:
1)c 0, где c const .
2)u x v x u x v x
52

3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u x v x |
u |
x v x u x v x |
|
|
|
|||||||||||
4) |
c u x c u x , при c const |
|
|
|
||||||||||||
|
|
u(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) |
|
|
|
u (x)v(x) u(x)v (x) |
в любой точке, в которой |
v x 0. |
|
|||||||||
|
|
v |
2 |
(x) |
|
|
|
|||||||||
|
v(x) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|||||||||||||||
Теорема7.1.3.(Опроизводнойсложнойфункции). Пусть дана |
сложная |
|||||||||||||||
функция |
z f g x . Пусть функция y g(x) имеет производную в точке |
|||||||||||||||
x0 , а функция |
z f y |
имеет производную в точке |
z0 f y0 . |
Тогда |
||||||||||||
сложная функция |
|
z f |
g x |
|
также имеет производную в точке |
x0 и |
||||||||||
zx (x0) |
f (y0)g (x0). |
|
Или |
zx zy yx . |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема |
7.1.4. |
(Производная |
обратной функции). |
Пусть |
функция |
|||||||||||
y f (x) |
определена в некоторой окрестности точки x0 и в точке x0 |
имеет |
||||||||||||||
конечную и отличную от 0 производную f (x0); пусть для функции y f (x)
существует обратная функция x f 1 y , |
непрерывная в соответствующей |
|||||||||||||||||||||||||||||||
точке |
y0 f (x0). |
Тогда |
в |
точке y0 |
|
эта |
обратная |
функция имеет |
||||||||||||||||||||||||
производную, равную |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
f (x0) |
. Или xy (y0) |
yx (x0) |
xy |
yx |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ТАБЛИЦА ПРОИЗВОДНЫХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
№ |
y x |
|
|
|
y x |
|
|
|
№ |
|
|
|
|
|
|
|
y x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y arccosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
y C |
|
|
0 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y arctgx |
|
|
|
|
|
1 x2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
y xn |
|
|
nxn 1 |
|
|
|
|
13 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y arcctgx |
|
|
|
|
1 x2 |
|
|
|
||||||||
3 |
|
y ax |
|
|
ax lna |
|
|
|
|
14 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y shx |
|
|
|
|
|
|
1 x2 |
|
|
|||||||
4 |
|
y ex |
|
|
ex |
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
chx |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y chx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
|
y lоga x |
|
|
lоgae |
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
shx |
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y thx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
y lnx |
|
|
1 |
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y cthx |
|
|
|
|
|
|
ch2x |
|
|
|
||||||||
7 |
|
y sinx |
|
|
cosx |
|
|
|
|
18 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh2x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
y arcshx |
|
|
|
|
|
|
|
|
||
8 |
y cosx |
sinx |
|
19 |
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
y arcchx |
|
|
|
1 x2 |
|
|||||
9 |
y tgx |
|
|
1 |
|
|
|
20 |
|
|
|
1 |
|
|
|
|
||||
|
|
|
cos2 x |
|
|
|
|
|
x |
|
1 |
|
|
|
x2 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
y arcthx |
|
|
|
|
|
|
|
|
||
10 |
y ctgx |
|
1 |
|
|
|
21 |
|
|
|
|
1 |
|
|
|
|
||||
|
|
sin2 x |
|
|
|
x |
|
1 |
|
|
|
1 x2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
y arccthx |
|
|
|
|
|
|
|
|||
11 |
y arcsinx |
|
|
1 |
|
|
|
22 |
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
1 x2 |
|
|
|
x |
|
1 |
|
|
|
1 x2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.2. Решение некоторых типовых задач, рассматриваемых в аудитории
7.2.1. Найти приращение функции y 2x2 5
в точке x0 3, если приращение независимой переменной Dх = 0,3.
Решение. y y(x0 x) y(x) y( 3 0,3) y( 3) y( 2,7) y( 3)
2 ( 2,7)2 5 2 ( 3)2 5 2 |
2,72 32 2(7,29 9) 3,42. |
|||||||||||||||||||||||
7.2.2. Найти приращение независимой переменной Dх, для которого прираще- |
||||||||||||||||||||||||
ние функции |
y |
1 |
|
|
в точке х0 |
= 4 равно |
1 |
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|||
Решение. По определению приращения функции |
|
|
|
|
||||||||||||||||||||
y y(x |
x) y(x ) |
|
1 |
|
1 Dх можно найти из уравнения |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
|
4 |
x |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
1 |
1 |
|
|
|
|
1 |
|
5 |
4 x 81 3,24 x 3,24 4 0,76. |
||||||||||||||
|
4 x |
|
|
|
4 x |
|
||||||||||||||||||
|
|
2 18 |
|
|
|
|
9 |
|
|
25 |
|
|
|
|
||||||||||
7.2.3. Вычислить производную функции y 3sinx 2lnx. |
|
|
|
|||||||||||||||||||||
Решение. |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
3(sinx) |
2(lnx) |
3cosx x . |
|
|
|
|
|||||||||||||||||
7.2.4. Продифференцировать функцию y 2x4 |
x 3. |
|
|
|
||||||||||||||||||||
Решение. |
y 2x4 |
|
|
|
x 3 2 x4 x 3 =8x3 |
|
1 |
. |
||||||||||||||||
|
|
2 |
x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|

7.2.5. Продифференцировать функцию y x2ex .
Решение. y x2ex x2 ex x2 ex 2xex x2ex xex 2 x .
7.2.6. Продифференцировать функцию y arcsinx x .
Решение. Применим правило вычисления производной частного от деления двух функций:
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
arcsinx |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
arcsinx |
|
arcsinx |
|
|
|
|
|
|
|
|
|
x |
1 x |
|
arcsinx |
|||
|
x x arcsinx |
|
|
1 x |
|
|
|
|
|
|||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
2 |
|
|
|
x |
2 |
|
x2 1 |
x2 |
|||||||
|
|
|
|
|
|
|
|
|
2x . |
|
|
|||||||
7.2.7. Продифференцировать функцию y cos ln12 |
|
|
|
|
|
|||||||||||||
Решение. |
Функцию y cos ln12 |
2x представим в виде цепочки |
|
|
|
|||||||||||||
элементарных функций: y cosu , u t12 , t lnz , z 2x . Производную данной функции вычислим по правилу дифференцирования сложной функции:
|
|
|
|
12t |
11 |
, |
|
|
1 |
, |
|
, тогда |
yx yuuttz zx , так как |
yu sinu , |
ut |
|
tz |
z |
zx 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
yx sinu 12t11 1z 2. Подставляя вместо u , t и z их выражения через перемен-
ную x , окончательно получим: yx 12x sin ln12 2x ln11 2x .
7.2.8. Продифференцировать функцию y ln5 tg3x . |
|
|
|
|||||||||||||
Решение. |
Сложную функцию |
|
y ln5 tg3x |
|
представим в виде цепочки |
|||||||||||
элементарных функций: |
y u5 , |
u lnt , |
t tg z , |
z 3x . По правилу вычисле- |
||||||||||||
ния производной сложной функции имеем y yuut tz zx , т. е. y 5u |
4 |
3 |
, |
|||||||||||||
|
t cos2 z |
|||||||||||||||
|
|
4 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
так как yu |
5u |
|
, ut t , tz |
|
|
, zx 3. Подставив вместо u , t и z их выра- |
||||||||||
|
cos2 z |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
|
|
|
|
жения через переменную |
x , получим: y |
30ln |
|
tg3x sin6x |
|
|
|
|||||||||
|
|
|
|
|
||||||||||||
7.2.9. Продифференцировать функцию y sin3 3x .
55
Решение. Сложную |
функцию y sin3 |
x |
|
представим |
|
в |
виде цепочки |
|
|
|
|
||||||
|
3 |
|
|
|
|
|
||
элементарных функций: |
y u3 , u sint , t |
x |
. По правилу вычисления произ- |
|||||
|
||||||||
|
3 |
|
|
|
1 |
|||
|
|
|
|
|
|
2 |
|
|
водной сложной функции имеем y yuut tx , так как yu 3u |
|
, |
ut cost , tx 3, |
|||||
то y 3u2 cos3 t . Подставив вместо u и t их выражения через переменную x ,
получим: y sin2 3x cos3x .
7.2.10. Продифференцировать функцию y arcsinx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Решение. |
y arcsinx x sin y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
yx arcsinx |
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
. |
|||||||||
|
|
|
sin y |
|
cos y |
|
|
1 sin2 |
|
|
|
|
1 sin2 arcsinx |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
y |
|
|
|
|
|
1 x2 |
||||||||||||||||||||||||||
7.2.11. Продифференцировать функцию y lnx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. |
yx lnx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
ey |
|
|
e |
y |
|
e |
y |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
7.2.12. Вычислить производную функции |
|
|
y cos ln(3x2 |
|
2) |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
y |
|
sin ln(3x |
2 |
2) |
(ln(3x |
2 |
|
|
|
sin ln(3x |
2 |
2) |
|
|
|
(3x |
2 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
2)) |
|
3x |
2 |
|
2) |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin ln(3x2 2) |
|
|
6x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
3x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7.2.13. Вывести формулу производной функции, обратной к функции y shx
Решение. |
Дана функция y sh x |
ex e x |
|
|
|
|
|
|
|||
2 |
, её производная |
y |
|
|
|||||||
|
(sh x) |
||||||||||
ch x |
ex e x |
0, для всех x R , следовательно, функция |
y sh x |
на всей |
|||||||
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
действительной оси монотонно возрастает и имеет обратную функцию, обо-
56

значаемую arshx . Уравнение задаёт эту обратную функцию неявным образом. Продифференцируем обе части по х: 1 ch y yx , откуда yx 1chy . Из соотношения выразим ch2 y sh2 y 1, а поскольку ch y 0 для всех x R , то
получим chy |
1 sh |
2 |
y , где shy x . Таким образом, |
|
|
1 |
|
|||||||
|
|
1 x2 |
||||||||||||
|
(arsh x) |
|
||||||||||||
7.2.14. Исходя из определения, найти производную функции |
|
|
|
|||||||||||
|
1 cos xsin 1 |
, x 0, |
в точке x 0. |
|
|
|
|
|
|
|||||
f x |
|
|
x |
|
|
|
|
|
|
|
||||
|
0, |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
Решение. По определению производная функции |
f |
x в точке x 0 равна |
||||||||||||
f 0 lim |
f x f 0 |
. |
Подставим значения |
|
функции |
|
в данный |
|||||||
|
|
|||||||||||||
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
предел: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos xsin |
x |
0 |
|
|
|
|
||
|
|
|
|
f 0 lim |
|
|
|
. |
|
|
|
|
||
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
Так как функция sin 1 |
– ограниченная, а x – бесконечно малая функция при |
|||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x 0, то по теореме о произведении бесконечно малой функции на ограни-
ченную имеем бесконечно малую величину xsin |
1 |
0 |
при x 0. Заменяя в |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
числителе бесконечно малую функцию 1 cos xsin 1 |
|
эквивалентной функ- |
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
xsin |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цией |
x |
|
и снова используя упомянутую теорему, получим |
|
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x2 sin |
2 1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 cos xsin |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
|
|
|
|
|
|
=lim |
|
|
|
x |
0. |
|
|
|
|
|
|
|
|
|
|||||
x 0 |
|
|
|
x |
|
|
|
x 0 |
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
7.3. Задачи для самостоятельного решения |
|
|
|
||||||||||||||||||||
7.3.1. y |
1 x3 |
. |
7.3.2. |
y |
|
|
|
1 |
|
|
. 7.3.3. y |
|
|
|
|
3 |
|
|
|
. |
||||||
1 x |
3 |
|
x |
2 |
x 1 |
1 x |
2 |
1 |
2x |
3 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |
|
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
2 |
5 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. 7.3.5. y 7x2 4 6 . 7.3.6. y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
7.3.4. |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
7.3.7. y |
2x |
3 |
3x |
2 |
|
6x 1 |
4 |
. 7.3.8. y |
|
|
x3 |
2x |
. 7.3.9. y |
|
|
|
|
|
|
1 |
|
|
|
|
. |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ex |
|
|
x |
|
|
a2 x2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
7.3.10. y |
|
|
|
sinx |
|
|
|
. 7.3.11. |
|
y 1 ex . |
|
|
7.3.12. y sin2 cos3x . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
1 cosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответы. 7.3.1. |
|
y |
|
|
6x2 |
|
|
. 7.3.2. y |
2x 1 |
. 7.3.3. y |
|
|
|
6x 1 3x 5x3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
1 2x |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
.7.3.4. y |
|
4 2x 1 |
|
|
. 7.3.5. y 6 14x |
4 |
7x2 |
4 6 5 |
.7.3.6. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
|
5 x2 2x 1 1 x2 4 |
. 7.3.7. y 24 |
|
x2 |
x 1 |
|
|
2x3 |
3x2 |
6x 1 |
|
|
3 |
|
.7.3.8. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y |
|
2x ln2 1 3x2 |
|
x3 |
. 7.3.9. |
y |
x |
|
a2 x2 |
|
.7.3.10. y |
|
|
1 |
|
|
|
|
|
|
|
|
7.3.11. |
|
|||||||||||||||||||||||||||||||||||||||
|
2ex |
|
|
|
|
ex |
|
|
|
|
|
|
|
|
|
|
a2 |
a2 x2 |
|
1 cosx |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
y |
|
|
|
. 7.3.12. 3sin3x sin 2cos3x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1 e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАНЯТИЕ 8.
8.ПРОИЗВОДНЫЕ ПЕРВОГО ПОРЯДКА
8.1.Логарифмическое дифференцирование и производная неявной
функции Логарифмическое дифференцирование
Иногда полезно использовать так называемую формулу логарифмического дифференцирования. Пусть f (x) 0 на некотором множестве значений
аргумента и дифференцируема на этом множестве. Тогда по формуле произ-
водной сложной функции имеем |
|
|
|
1 |
f |
|
|
f (x) |
|||||
|
(ln f (x)) |
(x), откуда |
||||
|
|
|
|
|
|
|
f (x) |
f (x) ln f (x) |
|
|
|||
Дифференцирование неявных функций
Пусть значения переменных x и y связаны между собой некоторым уравнением, которое, если все его члены перенести в левую часть, может быть
58
записано в виде |
F x,y 0, где F x,y некоторая функция двух пере- |
||
менных. Если для каждого значения |
x , принадлежащего некоторому мно- |
||
жеству |
X , существует одно значение |
y , принадлежащее некоторому мно- |
|
жеству |
Y , такое, |
что F x,y 0, то этим определяется некоторая функция |
|
y y x . Такая функция называется неявной функцией, заданной уравнением
F x,y 0. Тогда F x,y 0 x X Fx x,y x 0.
8.2. Решение некоторых типовых задач, рассматриваемых в аудитории
Найти производные функций:
8.2.1. |
y 3 |
x3 x2 1 |
|
5 5 x |
|||
|
|
Решение. Применим метод логарифмического дифференцирования. Логарифмируя данную функцию и применяя свойства логарифмов, получим:
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x2 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
||
|
ln |
|
y |
|
ln |
3 |
|
x |
|
|
1 |
|
ln |
|
x |
|
|
3ln x 1 15ln |
|
5 x |
|
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
5 |
5 x |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Продифференцируем обе части выражения и выразим y : |
|
|||||||||||||||||||||||||||||||||||
|
y 1 1 2x |
|
|
1 1 |
|
|
|
|
|
|
|
1 |
|
2x |
1 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x 3 x2 1 |
15 5 x , y |
y x 3 x2 1 15 5 x . |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
Подставив выражения для y , получим производную заданной функции:
|
|
|
3 |
|
|
|
|
x |
|
3 x2 1 |
1 |
|
2x |
1 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y |
|
|
|
|
|
|
|
|
5 |
|
5 x |
|
|
x |
3 x2 1 |
15 5 x . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
8.2.2. y |
(x 4)2 (x2 2)3 (3 2x)4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
3 (5x 1)2 |
|
|
|
|
. Решение. Аналогично предыдущему |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
примеру: ln y 2ln |
|
x 4 |
|
3ln x2 2 |
4ln |
|
3 2x |
|
|
2ln 5x 1 |
1ln 3x 1 . |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2ln 5x |
1 1ln 3x |
|
|
||||
y y |
2ln |
|
x 4 |
|
3ln x2 |
2 4ln |
|
3 2x |
|
|
|
1 |
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
3 |
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
4) |
2 |
(x |
2 |
|
2) |
3 |
(3 |
|
2x) |
4 |
2 |
|
|
2x |
|
4 |
|
2 |
|
|
2 |
|
1 |
|
5 |
|
|
1 |
|
1 |
|
3 |
|
|
|
(x |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||
|
3 (5x 1)2 3x 1 |
|
2 |
|
|
|
|
|
3 |
5x |
1 |
2 |
3x 1 |
||||||||||||||||||||||||
|
|
x 4 |
|
x |
2 |
3 2x |
|
|
|
|
|||||||||||||||||||||||||||
8.2.3. y cosx sin2x .Решение. |
y |
|
2cos2x lncosx sin2x |
sinx |
|
, |
|
|
|
|
|
|
|
||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosx |
|
|
|
|
|
|
|
|
|
|||||
y 2 cosx sin2x cos2x lncosx sin2 x . Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
cosx sin2x 2 |
cosx sin2x cos2x lncosx sin2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
8.2.4.y sinx x . Решение. Решение. Аналогично предыдущему примеру: y sinx x x lncosx sinx x lnsinx x ctgx .
8.2.5.y xx2 . Решение: y xx2 x2 lnx xx2 2x lnx x xx2 1 2lnx 1 .
8.2.6.x2 y2 4. Решение. Продифференцируем по x обе части данного урав-
нения,считая y зависящимот x : |
2x 2yy |
|
0, отсюдавыразим |
y |
|
: |
y |
|
|
x |
y |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.2.7. x2 xy y3 1. Вычислить yx |
|
в точке |
|
|
x 0, y 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Решение. |
Продифференцируем по x обе части данного уравнения, |
считая y |
||||||||||||||||||||||||||||||||||
зависящим от x : 2x y xy |
|
2 |
y 0, yx |
y 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3y |
|
|
|
|
|
. Подставив |
|
|
|
|
|
|||||||||||||||||||||||||
|
3y2 |
x |
|
|
|
|
|
|||||||||||||||||||||||||||||
значения x 0, y 1 в выражение производной, получим |
yx |
|
x 0, y 1 13 . |
|
|
|||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
8.2.8. x3 ln y x2ey |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0. Решение. |
Дифференцируя по x обе части уравнения |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
2 |
|
y |
|
|
|
|
|
|
y |
|
|
||||
и имея в виду, что y есть функция от x , имеем: 3x |
|
|
|
y x |
e |
|
y 2xe |
|
0 |
|||||||||||||||||||||||||||
|
y |
|
|
|||||||||||||||||||||||||||||||||
y |
|
|
2xey 3x2 y |
. y |
4 |
x 2 |
ctg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 x2 yey |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8.2.9. cos y 4y2 ex . Решение. Аналогично предыдущему примеру: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
sin y y 8yy e |
x |
; |
sin y 8y y e |
x |
y |
|
ex |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
sin y 8y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
8.2.10. ex |
2ey 2xy 1 0. Решение. ex 2ey y 2xy ln2 y xy 0 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
