917

∙

̅

̅

̅

∙

̅

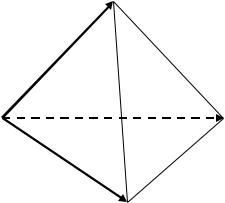
∙ пр ̅,

где

̅

, – площадь параллелограмма, построенного на векто-

рах

и ; пр

̅

для правой тройки векторов и пр

̅

для левой

тройки векторов, – высота параллелепипеда.

Получаем:

∙

̅

∙

,

где

– объ м параллелепипеда, построенного на векторах

, ,

̅.

Таким образом,

объ м параллелепипеда, построенного на векторах ,

,

̅, вычисляется по формуле:

парал.

.

В частности, объ м пирамиды, построенной на векторах

, , ̅

(рис. 2.45) вычисляется по формуле:

пир.

.

Рис. 2.45. Пирамида, построенная на векторах , ,

̅

2. Если смешанное произведение ненулевых векторов

, , ̅, равно

нулю, то векторы компланарны.

строить параллелепипед с ненулевым объ мом. Но так как

∙ ̅

, то

∙

̅ 0, что противоречит условию.

3. Если ненулевые векторы ,

,

̅компланарны, то их смешанное про-

изведение равно нулю.

Доказательство. Пусть векторы

,

,

̅компланарны.

Тогда вектор

̅

будет перпендикулярен плоскости, в которой лежат векторы , ,

̅, и, следовательно,

̅

̅

̅

0 и

∙ ̅ 0.

̅. Поэтому

∙

векторного и скалярного умножения:

∙ ̅ ∙

̅.

Доказательство. Из геометрических свойств можно записать:

∙

̅

и ∙

̅

̅∙

.

Знак в правой части этих равенств бер м один и тот же, так как тройки

векторов

, ,

̅и ,

̅,

одной ориентации. Следовательно,

∙

̅

∙

̅. Это позволяет записывать смешанное произведе-

ние векторов

∙

̅в виде

̅без знаков векторного и скалярного

умножения.

множаемых векторов

Векторы

, ,

̅заданы своими координатами:

; ;

,

; ; , ̅

;

; . Найд м смешанное произведение векторов ,

̅

̅

̅

∙ ̅

∙

̅

̅

̅

̅

∙

̅

̅

∙

∙

∙

.

7

2

3

̅

1

3

4

61.

9

3

1

Ответ: 61.

Пример 2.64. Выяснить, компланарны ли векторы

3 ̅ ̅ 7 ,

3

1

7

̅

5

4

3

0.

2

5

4

Так как смешанное произведение векторов равно нулю, то эти векторы

компланарны.

Ответ: векторы компланарны.

Пример 2.65. При каком значении

векторы

̅ ̅ ,

,̅ ̅

1

1

̅

0

1

0

1

3 .

3

0

1

Приравниваем полученное выражение к нулю: 1

3

0. Отсюда

.

Ответ:

.

Даны

точки

2; 3; 1 ,

4; 1;

2 ,

6; 3; 7

и

Пример 2.66.

5;

4; 8 . Найти объ м пирамиды

.

Решение. Объ м пирамиды, построенной на векторах, привед нных к

общему началу,

равен

модуля смешанного произведения этих векторов.

Рассмотрим векторы

,

и

, на которых построена пирамида

(рис. 2.46).

В условиях примера

пир.

|

|. Найд м координаты векто-

ров

,

и

, учитывая,

что при нахождении координат вектора нужно

из координат конца вектора вычесть координаты его начала:

4

2; 1

3;

2

1

2;

2;

3 ;

6

2; 3

3; 7

1

4; 0; 6 ;

5

2;

4

3; 8

1

7;

7; 7 .

Далее находим смешанное произведение векторов

,

и :

ствующей: cos

√

, cos

√

, cos

√

.

Задача 2.3. Три силы , ,

приложены к одной точке, имеют вза-

щей , если известны величины сил: |

| 3, | | 7, | | 4.

Решение. Так как по условию силы имеют взаимно перпендикулярные

направления, то векторы сил , ,

направлены по р брам прямоуголь-

бер, выходящих из одной точки. В условиях задачи получаем:

| |

|

|

| |

| | .

Подставляем значения величин сил:

| |

3

7

4

74.

Отсюда |

|

√74.

Ответ: √74.

Задача 2.4. Найти величину равнодействующей сил

и , если

| | 7, |

|

4; угол между силами и равен 120 .

(к Задаче 2.4)

Решение. Равнодействующая равна сумме заданных векторов сил

и :

. Найд м квадрат равнодействующей , используя алгеб-

| |

| | 2

| |

| | 2| | ∙ | | cos ,

| |

7

2 ∙ 7 ∙ 4 cos 120 4

37.

Отсюда |

| √

37

.

85

Ответ: √37.

Задача 2.5. Найти работу силы , если точка, на которую действует

сила, совершила перемещение в направлении вектора

̅. Известно, что | |

8, | ̅| 3,

, ̅ 30 . Указание. Работа силы

, когда точка, на которую

действует сила, совершила перемещение

̅, равна скалярному произве-

дению вектора силы на вектор перемещения

̅:

∙ ̅.

Решение. Работа

, совершаемая силой

в направлении вектора ̅

определяется как скалярное произведение векторов

и

̅:

∙ ̅. Исполь-

зуя определение скалярного произведения векторов, получаем:

|

| ∙ | ̅| ∙ cos

, ̅.

Подставляем числовые значения:

8 ∙ 3 ∙ cos 30

12√3.

Ответ: 12√3.

Задача 2.6. Найти работу силы

6;

3;

5 ,

если точка, на кото-

9; 7;

4 . Указание. Работа силы , когда точка, на которую действует сила,

совершила перемещение

̅, равна скалярному произведению вектора

силы

на вектор перемещения ̅:

∙ ̅.

Решение. Работа

, совершаемая силой в направлении вектора ̅

определяется как скалярное произведение векторов и ̅:

̅. Используя

наты, получаем:

6 ∙ 9

3 ∙ 7

5 ∙

4

53.

Ответ: 53.

Задача 2.7. Какую работу производит сила

7; 5;

2 , когда точка

е приложения перемещается из точки

1;

5; 1

в точку

2; 6; 4 ? Ука-

перемещение

̅, равна скалярному произведению вектора силы на

вектор перемещения

̅:

∙ ̅.

Решение. Найд м координаты вектора

,

вычитая из координат

конца вектора соответствующие координаты его начала:

3; 11; 3 . Ра-

бота , совершаемая силой

в направлении вектора

определяется как

скалярное произведение векторов и

:

∙

. Используя формулу

чаем:

7 ∙ 3

5 ∙ 11

2

∙ 3

70.

Ответ: 70.

Задача 2.8. Найти работу равнодействующей

сил

3 ̅ 6 ̅ 2

и

5 ̅ 4 ̅

при

перемещении

е

точки

приложения

из точки

6; 2; 5 в точку 7; 3; 2 . Указание. Работа силы

, когда точка, на ко-

торую действует сила, совершила перемещение

̅,

равна скалярному

произведению вектора силы

на вектор перемещения

̅:

∙

̅.

Решение. Равнодействующая

равна сумме заданных векторов сил

и

:

. Векторы

и заданы через разложение по ортам ко-

ординатных осей. Запишем координаты векторов

и

:

3; 6; 2 ,

5; 4; 1 . Далее воспользуемся правилом сложения векторов через их

координаты. Получаем:

3 5; 6

4;

2

1

8; 10;

3 .

86

Найд м координаты вектора

, вычитая из координат конца вектора

соответствующие координаты его начала:

13; 1; 7 . Работа

, совер-

шаемая силой

в направлении вектора

определяется как скалярное про-

изведение векторов и :

∙ . Используя формулу нахождения ска-

лярного произведения векторов через их координаты, получаем:

8 ∙ 13

10 ∙ 1

3 ∙ 7

93.

Ответ: 93.

Задача 2.9. Сила

2; 4; 5

приложена к точке 4; 2; 3 . Опре-

делить момент этой силы относительно точки

3; 2; 1 . Указание. Если

сила

приложена к точке

, то моментом силы

относительно точки

на вектор силы

:

.

Решение.

Найд м координаты вектора

, вычитая из координат

конца вектора соответствующие координаты его начала:

1; 4; 4 .

Момент силы

, приложенной к точке

, относительно точки

равен век-

торному произведению векторов

и

:

. Используя формулу

̅

̅

1

4

4

4 ̅ 3 ̅ 4 .

2

4

5

Получаем:

4; 3; 4 .

Ответ: 4; 3; 4 .

Задача 2.10. Сила

3; 4;

2 приложена к точке 2; 1; 2 .

сительно начала координат. Указание. Если сила

приложена к точке , то

моментом силы относительно точки

называется вектор , определяемый

как векторное произведение вектора

на вектор силы :

.

Решение. Начало координат – это точка

0; 0; 0 . Найд м коорди-

ординаты его начала:

2; 1; 2 . Момент силы , приложенной к

точке , относительно точки

равен векторному произведению векторов

и . В условиях задачи:

. Используя формулу нахождения век-

̅

̅

2

1

2

10 ̅ 2 ̅ 11 .

3

4

2

Получаем:

10;

2; 11 .

| |

10

2

11

15.